| [15] SmallPotato | 2009-08-20 03:24:50 |
 A teljesség igénye nélkül, egy listácska az első 22 ilyen hányadosról (a listázás befejezésének feltétele az volt, hogy az utolsó két számított hányados különbsége kisebb legyen, mint 10-9):
Látható, hogy már a 3/8 is 0,01 pontosságú, a 13/34 pontossága pedig már 0,001.
A pontos érték egyébként  .
|
| Előzmény: [14] SmallPotato, 2009-08-19 23:42:51 |
|
| [14] SmallPotato | 2009-08-19 23:42:51 |
|
A jelenlévők többsége nyilván tudja ezt, de hátha lesz errejáró, akinek új: ezek a visszatérő meredekségek az F(n) és F(n+2) Fibonacci-számok hányadosával "definiálhatók". Hogy sűrűn találkozunk velük ilyen terület-elcsalós feladatokban, annak bizonyára az az oka, hogy  létezik és a konvergencia "elég gyors", vagyis a hányadosok már kis n esetén is "egymáshoz elég közel vannak" ahhoz, hogy szemmel ne tudjuk megkülönböztetni őket.
|
| Előzmény: [12] HoA, 2009-08-19 08:30:00 |
|
|
| [12] HoA | 2009-08-19 08:30:00 |
 Hogy Sirpit idézzem: mert "2/5, 3/8 és 5/13 számok bár kellően közel vannak egymáshoz, mind különbözőek." :-)Érdekes, hogy itt ugyanazok a meredekségek lépnek fel, mint [1] -ben. ( Amúgy a jobb oldali persze nem négyzet. )
|
| Előzmény: [10] jonas, 2009-08-18 23:03:03 |
|
|
| [10] jonas | 2009-08-18 23:03:03 |
 Nekem ebből a fajtából ez a kedvenc feladatom -- biztos, sokan ismeritek.
A bal oldali négyzet területe 64, a jobb oldalié 65, mégis átdarabolhatóak egymásba, miért?
|
 |
|
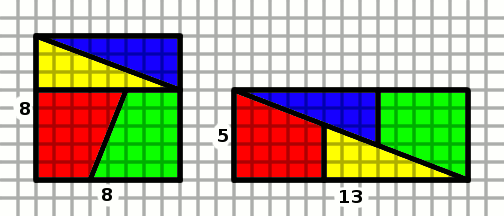| [9] HoA | 2009-08-03 09:33:08 |
|
Hogy ne csak meggyőzzünk, hanem értsd is: Itt egy durvább változat. Itt ránézésre is világos, hogy nem két háromszögről, hanem egy konvex és egy konkáv négyszögről van szó. Miért kéne, hogy egyenlő legyen a területük? A területek közötti különbség éppen a lenti négy kis fehér négyzet területe.
|
 |
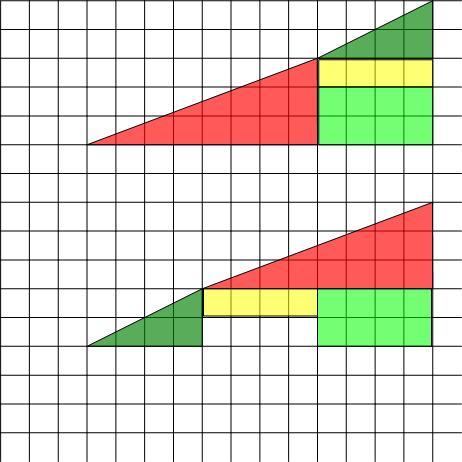| Előzmény: [7] Rasmus, 2007-04-12 18:23:59 |
|
| [8] bicikarcsi | 2009-07-30 17:02:54 |
 Sziasztok. referatumot irnek "Nevezetes pontok közötti távolságok" cimmel. ha van, legyszi kuldjetek valami anyagot hozza. koszike
|
|
| [7] Rasmus | 2007-04-12 18:23:59 |
|
Köszönöm ! Nem állítom , hogy teljes mértékben értem de nekem ennyi elég , meggyőztetek.
Irigylem az agyatok ! :-)
|
|
|
| [5] Sirpi | 2007-04-12 10:14:06 |
 Tudom, hogy nem írtam részletes indoklást, de egyrészt elég késő volt, másrészt meg úgy gondoltam, kicsit gondolkozzon el előbb, hogy miért írhattam azt, amit, és ha még mindig nem áll össze neki, akkor adunk neki még egy kis segítséget. Mindenesetre köszönöm a kiegészítést :-)
Még annyit tennék hozzá, hogy ha 180 fokkal elforgatjuk a "háromszögeket" az "átfogójuk" felezőpontja körül, akkor a fenti esetben az eredeti és elforgatott példány között egy egységnyi területű paralelogramma alakú lyuk lesz, míg a második esetben a két "háromszög" egy ezzel egybevágó paralelogrammában fogja metszeni egymást.
|
| Előzmény: [4] lorantfy, 2007-04-12 08:40:05 |
|
| [4] lorantfy | 2007-04-12 08:40:05 |
 Attól tartok Rasmus ebből még nem értette meg miről van szó! Ezek az idomok nem háromszögek. A leghosszabb oldaluk ugyanis nem egyenes. Ha odatartod a vonalzódat a monitorhoz rögtön látszik. Ezt úgy láthatjuk be, hogy összehasonlítjuk a háromszögek átfogóinak meredekségét, vagyis a függőleges és vizszintes befogók hányadosát. Ezek a Sirpi által leírt törtek.
|
| Előzmény: [2] Sirpi, 2007-04-12 01:18:29 |
|
|
|
| [1] Rasmus | 2007-04-12 00:48:05 |
|
Sziasztok! Nem akarlak bennetek nagyon fárasztani , de volna egy feladat ami megoldásra várna. Lehet , hogy már találkoztatok vele , de mivel tőlem a matek meg a mértan sajnos elég távol áll ezért kérném a segítségeteket. A feladat ( ami lehet,hogy csak számomra feladat):
|
 |
|
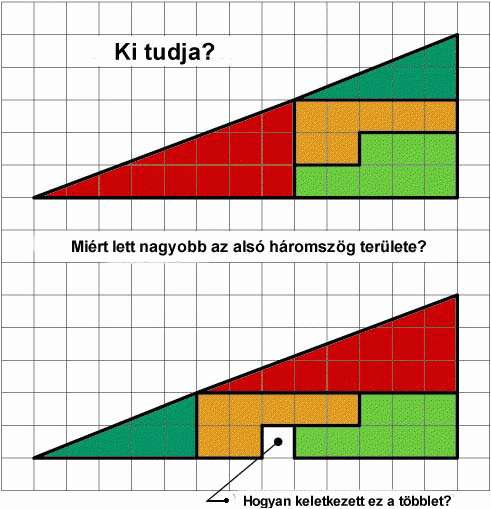