Fórum: Grafi-logikai feladványok

Nagyon köszönöm jonas a gyors választ!

Kicsit szégyenlem magam, amiért nem jöttem rá. :)

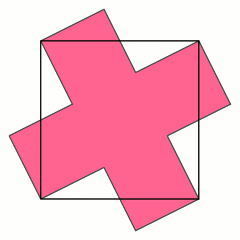
Próbálj meg a kocka minden oldalára egy-egy keresztet rárakni ferdén, az alábbi ábra szerint. A kereszt négy csúcsa a kocka lapjának egy-egy csúcsába esik, a másik négy csúcs túlnyúlik a szomszédos lapokra.

Sziasztok!

A Matkönyvben találtam ezt a feladatot, és eléggé sok fejtörést okozott, de nem sikerült megcsinálnom. Tudnátok segíteni benne?

Feladat: 12.23. (S) Be lehet-e burkolni egy kocka felületét hézagtalanul és egyrétűen 6 olyan egybevágó kereszt alakú papírral, amelyik mindegyike 5 egybevágó négyzetből áll, és egy „kereszt” területe egyenlő egy kockalap területével? A papírlapokat szétvágni nem lehet, csak behajtani.

Próbáld meg ugyanennek a témának az elejét megnézni, vagy esetleg a Találjunk jobb megoldást! témát.

Mivel egy újoncnak minden feladat új, ezért tudnátok hasonló, de könnyebben megoldható gyakorló feladatokat feltenni? Csak négyzetrács mellett lehessen tagolni. Nagyon érdekes a téma, és egy hasonló feladat eddig kifogott rajtam, de meg szeretném oldani...

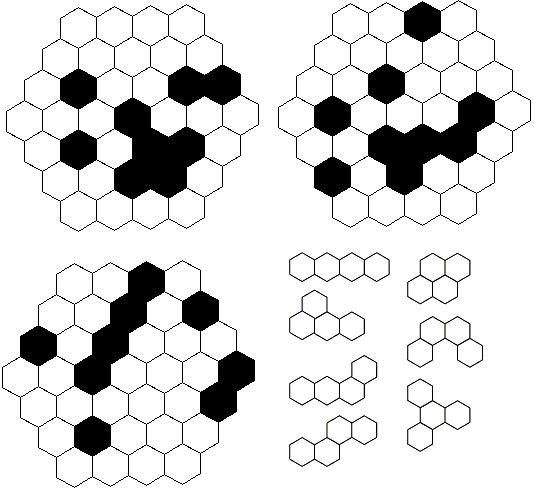
Egy újabb rajzolgatós, darabolgatós feladat.

42.feladat Helyezze el az alábbi hét alakzatot minden ábrában. (Az alakzatok nem fedhetik egymást, és nem lóghatnak ki, valamint nem kerülhetnek fekete mezőre sem) Forgatni lehet őket, de tükrözni nem.

A feladatokat Madarassy Pál készítette.

Az első nem nehéz.

Üdv! Megoldottam az eddig még megoldatlan 36-ost. Viszont nem hiszek abban, hogy érdemes lenne direktbe lelőni, úgyhogy csak így rakom be, hogyha 1év múlva ismét betéved valaki, akkor foglalkozhasson vele :)

36.feladat megoldása

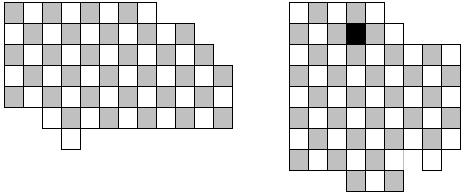
És ahogy ígértem hoztam új feladatot

41. feladat Vágja szét az ábrát a négyzetek oldalai mentén úgy, hogy a két darabból egy sakktáblát lehessen összerakni. (A második ábrában a fekete mező lyuk a papíron.) Továbbá a papír egyoldalas, így a kapott két alakzat csak forgatható, de nem tükrözhető.

Üdv!

Hajba Károly emailben megírtam az észrevételemet a rejtvényekről. Illetve ide is felrakok pár feladatot, hátha érdekel valakit. Hamarosan hozok olyat, ami a topik címéhez is illik. :)

http://filekeeper.org/download/shared/antimagikus.pdf

A módosított feladat megoldása:

Nekem személy szerint nagyon tetszenek ezek a feladatok (Legyen mindig 9, Legyen minden szám csak 1x, Szétszakadt vonallánc), és megoldhatók próbálgatás nélkül is (én mindet úgy csináltam)

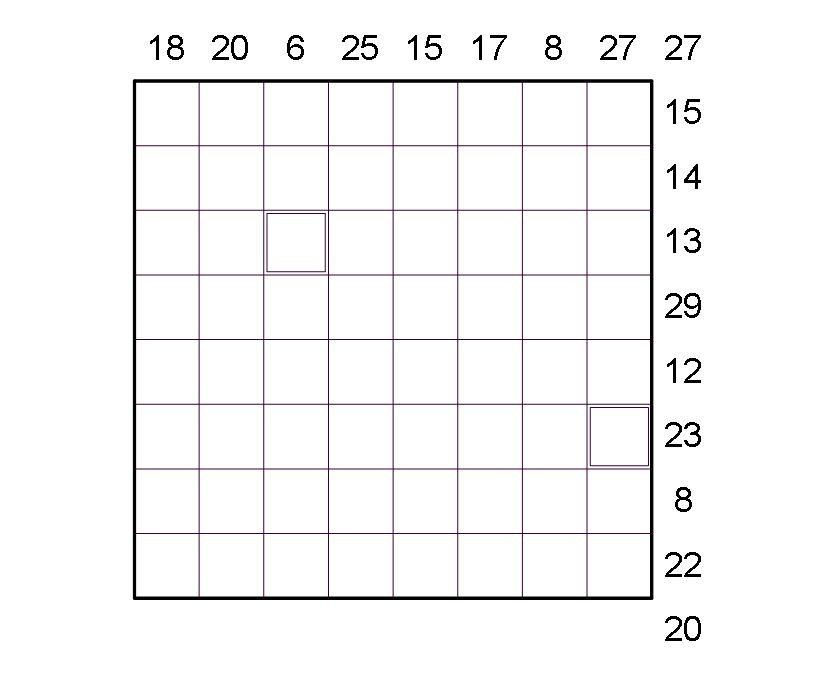
Jogos. Valóban elszámoltam, s először nem is tűnt fel. Ezért elnézést!. Elvileg az oszlopok tetején lévő számok összegének meg kell egyeznie a sorok végén lévők összegével és ez az 1-n szummával. Jelen esetben 136-tal. Így a helyes feladat:

Jogos. Elütöttem. A 39. feladat kitűzése helyes. Persze ez egy kísérletezés, s nem tudom, hogy nagyobb számokkal, hogyan oldható meg. Magamat nagyon nehéz ellenőrizni ebben az esetben. A kísérleti nyúl szerepeteket meg előre is köszönöm. :o)

---

Az archívum rendetlen működését már én is tapasztaltam.

A feladatötleteimmel kapcsolatban minden észrevételt szívesen várok, akár magánban is. Észrevételeiteket előre is köszönöm.

Azt hiszem Gergely nem a 40-es, hanem, a 39-es feladat kiírását vélte hibásnak.

Ceterum censeo: Ki tudja, miért nem működik a sulinet KöMaL archívuma?

A következő és itt korábban már betett feladatok saját alkotásaim. Ha valaki már korábban találkozott már ilyennel, kérem jelezze, hogy tudjak róla.

Amennyiben nincs már korábbi szerzője, úgy a nem KöMaL-os felhasználás esetén a Nevezd meg!-Ne add el! 2.5 Magyarország elv betartását kérném velük szemben.

Komplementer dominó

Legyen mindig 9

Legyen minden szám csak 1x

Szétszakadt vonallánc

A Hurokkereső-t a Logika újságban találtam, míg a Ossza szét típusú feladatok klasszikusok.

18., 37., 38. feladatok megfejtése helyes.

40. feladat kiírása megfelelő, visszaellenőriztem.

Szerintem sincs megoldása.

18. feladat megoldása

Ha jól láttam ezt a feladatot még senki nem oldotta meg

A 40-esnek is megvan a megoldása, egyelőre még várok, hátha más is megoldja. A 39-es feladat nincs véletlenül elírva? Folyamatosan ellentmondásra jutok.

38. feladat megoldása:

37. feladat megoldása:

Néhány próbálkozás után a következő lett a megoldás (remélem jó):

40. feladat: Szétszakadt vonallánc

Feladatleírás: Szétszakadt vonallánc

Az adott áttetsző lapocskák közül kettő esetleges forgatás és tükrözés után oly módon illesztkedik, hogy a vonalak zárt, folytonos, nem elágazó és átfedő láncot alkotnak.

39. feladat: Legyen minden szám 1x - (1 - 16)