|
| [74] Makay Géza | 2024-07-27 10:30:19 |
 13. kérdés: A válasz igen.
Bizonyítás: Nyilván nincs jelentősége, hogy a sokszög szabályos legyen, elegendő az is, ha konvex, hogy tényleg belső háromszögek alakuljanak ki az átlók behúzásával. Azt fogjuk belátni teljes indukcióval, hogy minden háromszögelés átlócserékkel átvihető egy olyan háromszögelésbe, ahol az egyik kijelölt csúcsból induló átlókkal (és csak azokkal) háromszögeltük a sokszögünket. És ez elegendő a feladat állításának belátásához is, hiszen ha az első háromszögelést átalakítjuk így, akkor a második háromszögelés hasonló átalakítását visszafelé lejátszva megkapjuk a két háromszögelés egymásba alakítását.
Háromszögre az állítás triviálisan igaz. Tegyük fel, hogy \(\displaystyle n\)-szögekig igaz az állítás (\(\displaystyle n\geq 3\)). Jelöljük ki egy csúcsot egy \(\displaystyle (n+1)\)-szögben. Ha abból indul ki átló, az két részre bontja az \(\displaystyle (n+1)\)-szöget, az indukciós feltevés szerint azok átalakíthatóak úgy, hogy csak a kijelölt csúcsból induló átlók legyenek behúzva. Ha a kijelölt csúcsból nem indul átló, akkor a két szomszédos csúcs kell legyen átlóval összekötve, erre alkalmazzuk az átlócserét, és máris indul ki átló a kijelölt csúcsból. Ezzel beláttuk az állításunkat \(\displaystyle (n+1)\)-szögekre is.
|
| Előzmény: [70] Róka Sándor, 2024-07-23 08:04:59 |
|
| [73] Róka Sándor | 2024-07-23 18:39:27 |
 Várhattam volna a Dagobert bácsis feladat megoldásával (69. hsz.), talán a 34. hozzászólásommal is ...
Most vannak válasz nélküli, megoldatlan kérdések, ha ezek elfogynak, hozok újakat.
Kíváncsi vagyok mi a válasz a 4 sakkos feladatra (8–11. kérdések), és azt hogyan indokoljátok. Én nem ismerem a válaszokat. A 12–13. megoldását ismerem, de csendben leszek ...
Hátha lesz még hozzászólás Dagoberthez is.
|
| Előzmény: [71] Sinobi, 2024-07-23 14:14:49 |
|
|
| [71] Sinobi | 2024-07-23 14:14:49 |
 Kicsit kár, hogy lelőtted, még mielőtt érkezett volna (jó) megoldás. (Engem különösen zavarnak a beküldött megoldásokban a feltevések a stratégiákat illetően, de ez lehet hogy csak az én vesszőparipám, hogy szeretem őket kimondva és belátva látni.) Biztosan van még másik bizonyítás is, szerintem például amit nadorp csinált is javítható.
Ez a bizonyítás működik kártyák tetszőleges \(\displaystyle d_1 >= d_2 >= .. >= d_n \) sorozatára. Jelölje \(\displaystyle A(d_i)\) azt az értéket, amit a Dagobert kap (a bank fizet), ha Dagobert minden körben \(\displaystyle d_i\)-t kér. (\(\displaystyle d_i\) egy kártyaérték.) Világos, hogy Dagobert el tudja érni \(\displaystyle A(d_i)\) maximumát a bank tetszőleges stratégiája esetén: minden körben \(\displaystyle d_i\)-t kér. Az is világos, hogy \(\displaystyle A(d_i)\) egy fix \(\displaystyle d_i\)-re úgy néz ki, hogy a \(\displaystyle d_i\)-nél nagyobbegyenlő értékű kártyák száma (jelölje \(\displaystyle N(d_i)\)), szorozva \(\displaystyle d_i\)-vel.
És az is teljesül, hogy ha a bank az általad felvázolt mohó stratégiát követi, akkor, Dagobert bármely stratégiájára valami \(\displaystyle A(d_i)\) értéknél nem többet fizet ki. Speciálisan az \(\displaystyle A(d_i)\) értékek maximumánál nem többet.
Még egyszer, a bank stratégiája: ha el tud utasítani, elutasít, ha el kell fogadnia, akkor a legnagyobb kártyával fogad el.
Ez elsőre furán néz ki, Dagobert 2-vel indít, és a bank ahelyett hogy kifizetné a 10-essel, inkább kidobja az 1-es kártyát. Mindenesetre ez egy jó stratégiája a banknak.
Bizonyítás: legyen G egy tetszőleges lejátszott játék, amit a bank e szerint a stratégia szerint játszott. Legyen \(\displaystyle d_i\) a legkisebb olyan kártya értéke, amellyel a bank fizetett valamennyit. Ekkor a bank nem használt \(\displaystyle d_i\)-nél kisebb kártyákat (mert \(\displaystyle d_i\) a legkisebb), és a bank nem fizetett \(\displaystyle d_i\)-nél többet (azt csak korábbi kártyával tehette volna meg, de akkor még megvolt a \(\displaystyle d_i\) értékű kártya, szóval el tudta volna utasítani a kérést). Tehát a bank maximum \(\displaystyle N(d_i)\)-szer fizetett egyáltalán, és minden körben maximum \(\displaystyle d_i\)-t, ez nem nagyobb, mint \(\displaystyle N(d_i) \cdot d_i = A(d_i)\).
És akkor nem is kellett számolni, mert csak azzal operáltunk, hogy milyen alakú Dagobert maxminje és a bank minmaxa.
|
| Előzmény: [69] Róka Sándor, 2024-07-22 22:04:31 |
|
| [70] Róka Sándor | 2024-07-23 08:04:59 |
 Két új kérdés, a Héttusa feladataihoz csatlakozva.
Sokféle szép megoldás érkezett a 28-as feladatra.
28. A hét törpe körbeüli az asztalt, és Hófehérke mindegyiknek annyi cukorkát ad, ahány hüvelyk a különbség a törpe két szomszédjának magassága között. Legfeljebb hány cukorkát oszthat szét közöttük Hófehérke, ha a törpék magassága 31, 32, 33, 34, 35, 36 és 37 hüvelyk?
(Hasonló feladat a KöMaL-ban F.2280. és P.364.)
Mi a válasz, ha nem körben, hanem sorban állnak?
12. kérdés: Hét gyerek ül egy mozi nézőterén az első sorban egymás mellett. Ha kiszámoljuk a szomszédos gyerekek közti (pozitív) magasságkülönbséget, és ezeket összeadjuk, megkapjuk az ülésrend magasságát. Mekkora lehet ennek a magasságnak a legnagyobb értéke, ha a gyerekek magassága valamilyen sorrendben 131, 132, 133, 134, 135, 136 és 137 cm?
A Héttusa 33-as feladata:
33. Egy 12-oldalú szabályos sokszögnek legfeljebb hány átlóját tudjuk megrajzolni úgy, hogy bármelyik legfeljebb egy másikat metszhet a sokszög belsejében?
Várható egy hasonló kérdés a következő fordulóban is, most azt nézzük, hogy két háromszögelés között van-e 'átjárás'.
13. kérdés: Egy 12-oldalú szabályos sokszög egy háromszögelését megkapjuk úgy, hogy egymást nem metsző átlókat rajzolunk, összesen 9 átlót, és így a sokszöget háromszögekre daraboltuk.
Ha töröljük két szomszédos háromszög közös oldalát (egy átlót), akkor a két háromszög helyén egy négyszög keletkezik. Rajzoljuk meg a négyszög másik átlóját, így az előző háromszögelésből kaptunk egy új háromszögelést. Nevezzük ezt a műveletet átlócserének.
Igaz-e, hogy alkalmas átlócserékkel a sokszög bármelyik háromszögeléséből bármely másik háromszögelést megkaphatjuk?
|
| Előzmény: [57] Róka Sándor, 2024-07-18 06:27:32 |
|
| [69] Róka Sándor | 2024-07-22 22:04:31 |
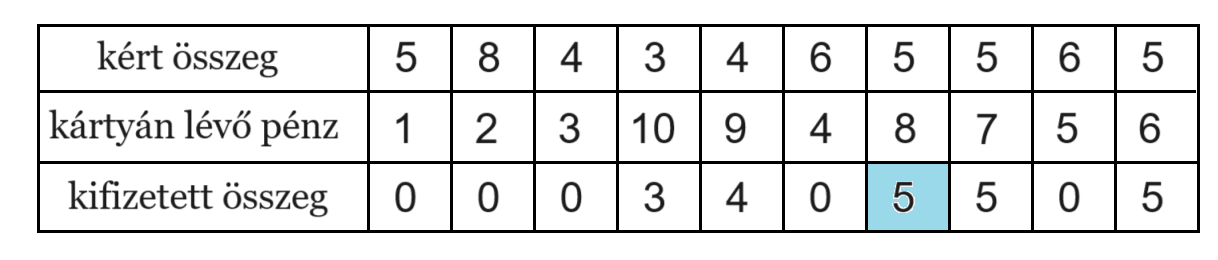
 7. kérdés, Dagobert bácsi.
Nézzük a bank startégiáját (Sinobi Gonosz manója). A bácsi megmondja mennyi pénzt akar felvenni, és odaad egy kártyát. A kártya értékét a bácsi nem tudja, így a bank választja meg, hogy azon milyen fedezet van.
(1) Ha a kért összegnél van kisebb értékű kártya, akkor azok egyike lesz a tranzakciónál használt kártya. Ez azt jelenti, hogy a bácsi nem kap pénzt, és ez a kártya már nem használható.
(2) Ha a kisebb értékű kártyák elfogytak, akkor a még érvényes kártyák közül a legnagyobb értékűt használjuk, és a bácsi megkapja a kért összeget.
A táblázat mutat egy példát a pénzfelvételre, a bank eljárására.
A kifizetett összegek közül válasszuk a legnagyobbat, \(\displaystyle m\)-et, és ha több ilyen összegű kifizetés van, akkor közülük az elsőt. Most \(\displaystyle m=5\).
Ez az \(\displaystyle m\) összeg kifizetésre került, tehát a nála kisebb értékű kártyák már elfogytak. (Ha lett volna ilyen kártya, akkor a bank ezt választja és nem fizet.)
A bank a kifizetéseknél a legnagyobb értékű kártyákat használja el, a (2)-es protokoll alapján. Tehát az \(\displaystyle m-1\) db kisebb értékű kártya felhasználásakor nem történt kifizetés.
Legfeljebb \(\displaystyle 10-(m-1)=11-m\) esetben történt kifizetés, és az ilyenkor fizetett összeg \(\displaystyle m\)-nél nem nagyobb.
Így az ATM-ből Dagobert bácsi legfeljebb \(\displaystyle (11-m)\cdot m\) ezer dollárt vehet ki. Mivel \(\displaystyle m\) egész szám, ezért a szorzat legnagyobb értékét \(\displaystyle m=5\), illetve \(\displaystyle m=6\) esetén kapjuk, ez a maximum 30 (ezer dollár).
A feladatot lehetne variálni. A kártya egyszeri használata marad, ám használat után az ATM blokkot ad, és akkor kiderül, milyen összeg volt a kártyán. (Esetleg csak pénz kifizetése esetén adja a blokkot.) Más változata az eredetinek, ha minden kártya kétszer használható.
|
 |
| Előzmény: [64] Sinobi, 2024-07-20 20:13:15 |
|
|
|
| [66] Róbert Gida | 2024-07-20 23:22:02 |
 Re64, re65.
Például legyen a tipp k=5 (ezer), és a még bent lévő kártyák 6,7,9 (ezer). Ekkor, ha a bank elfogad, akkor optimális stratégia szerint a 9 ezres kártyát használná fel a bank. Ha te azt mondod, hogy használjuk fel (mondjuk) a 6 ezrest, akkor tekintsd a még bent lévő kártyák rendezett sorrendjét, könnyen látható, ha nem opt stratégia szerint mész, akkor a te sorrendedben levő i-edik kártya legalább akkora mint az opt stratégia szerinti i-edik kártya, minden i-re. És minden lépésben csak veszítesz, legalábbis nem jársz jobban.
0 és 11 (ezres) tipp nem túl értelmes példa, ha 0-t mond akkor mindig el kell fogadni, 11 ezernél meg elutasítani. Ezt abból lehet könnyen látni, hogy 1-től 10 ezerig vannak a kártyák. Es ekkor persze a banknak sincs túl sok stratégiája, a játékos meg stabil nullát nyer. De mintha ezzel kezdtem volna az előző hozzászólásomat.
Meglepő, de értem a problémát. Ott van a hiba, hogy nagy ritkán teljesül az, hogy az optimális stratégia az a legjobb stratégia egy adott fix stratégia ellen. Példa1: fizetős gyors sakk játékomban a vesztes fizet \(\displaystyle \frac{1}{n}\) dollárt a győztesnek ha n-edik lépésben kap mattot, döntetlen esetén nincs fizetés. Gipsz Jakab ellen játszva észrevettem, hogy a bolondmattot nem ismeri, sőt mindig belemegy. Marha jó, n=2 lépésben mattot tudok adni, és betegre keresem magam a játékonkénti 50 centtel.
Megkeresett pénzből fölhalmozok jó sok kvantumbitet, sakk problémáját megoldom, kiderül, hogy tényleg a fehérnek van nyerő stratégiája, de csak h3-mal kezdve, és legrövidebben n=50 lépésben. Kiprintelem a teljes játékfát, megtanulom, és Carlsent legyőzöm az 50-dik lépésben, 2 centet keresve. Legyőzném-e n=2 lépésben? Aligha, sőt, mivel nem h3-mal kezdenék akkor nem is biztosan győznék.
Példa2: kő-papír-ollóra dettó ugyanez, (ebből egyébként világbajnokság is van). Egy forintot fizessen a vesztes játékonként, döntetlen esetén nincs fizetés. Mi itt az optimális nyerő stratégia? Ez a legjobb stratégia az ellen a játékos ellen is, aki mindig papírt mutat ?
|
| Előzmény: [64] Sinobi, 2024-07-20 20:13:15 |
|
| [65] Sinobi | 2024-07-20 20:17:23 |
 Bőven lehet, hogy Dagobert stratégiája mondjuk olyan, hogy ha az 5-ödik lépésben elfogadja a bank a kérését, akkor utána feladja, és csak 0-t vagy 11-et kér. A banknak ilyenkor megérheti nem ellőni az összes nagy kártyát az elején, hogy el tudja fogadni az 5-ik kérést, és ne kelljen elutasítania.
|
|
| [64] Sinobi | 2024-07-20 20:13:15 |
 Amúgy ha ezt
> Mit csinálhat a bank (ATM)? (Gonosz manó stratégiával): Ha a játékos (Dagobert) k (ezer) dollárt kér és a bank elfogadja az igényelt összeget, akkor ezt tegye úgy, hogy a legnagyobb még nem felhasznált kártyának tekinti a betett kártyát, feltéve hogy ez legalább k ezer dollár, ha ilyen nincs akkor mindenképpen elutasít a bank.
> Vagy a bank elutasítja a kártyát, ekkor a legnagyobb, de még k ezernél kisebb összegű kártyának tekinti a betett kártyát, ha ilyen nincs akkor mindenképpen el kell fogadni az igényelt összeget.
kihasználtad, akkor meg kéne indokolnod, hogy miért használhatod ki...
|
|
| [63] Róbert Gida | 2024-07-20 19:32:14 |
 7. feladat (Dagobert bácsi 10 bankkártyája). Programmal: n=10 kártyára a 30000 dollár a maximum, és nadorp tippje n=25-ig biztosan igaz.
Trivi módon Dagobert csak k=1,2,..,n (ezer) dollárokat fog kérni (például 2650 dollár helyett jobb kérni 3000-et).
Mit csinálhat a bank (ATM)? (Gonosz manó stratégiával): Ha a játékos (Dagobert) k (ezer) dollárt kér és a bank elfogadja az igényelt összeget, akkor ezt tegye úgy, hogy a legnagyobb még nem felhasznált kártyának tekinti a betett kártyát, feltéve hogy ez legalább k ezer dollár, ha ilyen nincs akkor mindenképpen elutasít a bank.
Vagy a bank elutasítja a kártyát, ekkor a legnagyobb, de még k ezernél kisebb összegű kártyának tekinti a betett kártyát, ha ilyen nincs akkor mindenképpen el kell fogadni az igényelt összeget.
Hogyan lép a bank? Azt választja (elfogad/eluasít), amivel minél kevesebbet kell fizetni.
A játékos pedig azt a k értéket választja k=1,2,..,n közül, amire neki maximális(!) lesz a nyereménye. És ekkor persze a bank a számára minimálisan kifizetendő esetet választja.
"Csak" \(\displaystyle 2^{n}\) eset van, hiszen n darab bankkártyának ennyi részhalmaza van. Az alapeset amikor nincs már kártyája ekkor 0 a nyeremény. Egyébként pedig dinamikus programozással megoldható.
Bank persze játszhat nem optimális módon, tehát mégsem tudnánk, hogy milyen kártyáink vannak még, de ez a játékosnak csak jó, hiszen ekkor még többet nyerünk. Ugye itt kevert stratégiák is elképzelhetőek, de ez a számolást nem befolyásolja, hiszen optimális tiszta stratégia itt mindig lesz.
|
| Előzmény: [41] Róka Sándor, 2024-07-14 22:22:50 |
|
|
| [61] Sinobi | 2024-07-20 09:06:46 |
 Hát én ebből abszolút semmit nem értek. Nincs meg a távoli, vázlatos kép, hogy mit csinálsz. A jelekből meg az eszközökből ítélve a kártya permutációk és a pénz kérelmek szorzathalmazán minimalizálsz, de az elvi hiba, hiszen egy pénzfelvétel kérelemhez nem tartozik az összes lehetséges kártya permutáció. Dagobert bácsi módosíthatja a pénzfelvétel kérelmi stratégiáját időközben. Például Dagobert bácsi bátran, 10-zel kezd, és ha megadja az ATM, akkor 9-cel folytatja, majd 8-cal, majd 7-tel sít. Ha nem adja meg az ATM, akkor megijed, és végig 1-et kér. Ekkor a (10,9,8,..) kérelmekhez nem mondhatod hogy a (9,8,7..) kártya adatok nagyon rosszak, hiszen ilyen helyzet nem áll elő, köszönhetően Dagobert bácsi stratégiájának.
|
| Előzmény: [59] nadorp, 2024-07-19 21:12:31 |
|
|
| [59] nadorp | 2024-07-19 21:12:31 |
 7. kérdés
Állítás: n db bankkártya esetén, melyeken valamilyen sorrendben rendre 1,2,3,...,n ezer dollár van, legalább \(\displaystyle 1000\left[\frac{(n+1)^2}4\right]\) ([...] = egész rész) dollár vehető fel.
Tegyük fel, hogy az i-dik lépésben betett kártyán \(\displaystyle d_i\) dollár van és \(\displaystyle x_i\) (\(\displaystyle x_1\geq0\) egész) dollárt akarunk felvenni. Ekkor összesen
\(\displaystyle \sum_{i=1}^n \lambda_ix_i\) összeget tudunk kivenni, ahol \(\displaystyle \lambda_i=\left\{\matrix{ 1\ ha\ x_i<=d_i\\0 \ ha\ x_i>d_i}\right.\)
Ha P jelöli az 1000,2000,..,1000n számok összes permutációjának halmazát, akkor egy adott \(\displaystyle \{x_i\}\) pénzfelvétel sorozat esetén legalább
\(\displaystyle m(x_1,...,x_n)=\min_{(d_1,d_2,...,d_n)\in P}\sum_{i=1}^n \lambda_ix_i\) összeg vehető fel. Ennek az \(\displaystyle m(x_1,...,x_n)\) függvénynek keressük a maximumát.
Először is nyilván a maximum olyan \(\displaystyle \underline x=(x_1,...,x_n)\) esetén érhető el, ahol \(\displaystyle x_i\leq1000n\) minden i-re, hiszen ha valamelyik \(\displaystyle x_i>1000n\), akkor ezt 1000n-nel helyettesítve olyan \(\displaystyle \underline x'\) pénzfelvétel sorozatot kapunk, melyre az \(\displaystyle m(\underline x')\) előállításban szereplő mindegyik összeg legalább akkora, mint a neki megfelelő \(\displaystyle m(\underline x)\)-ben szereplő összeg.
Másrészt ha valamelyik \(\displaystyle x_i\leq1000n\) nem 1000k alakú, akkor ezt a hozzá legközelebb álló, nála nagyobb 1000-rel osztható számmal helyettesítve olyan \(\displaystyle \underline x'\) pénzfelvétel sorozatot kapunk, melyre az \(\displaystyle m(\underline x')\) előállításban szereplő mindegyik összeg legalább akkora, mint a neki megfelelő \(\displaystyle m(\underline x)\)-ben szereplő összeg.
A fentiekből következik, hogy maximum akkor lehet, ha \(\displaystyle x_i=1000k\) (\(\displaystyle 0\leq k \leq n\)). Az ilyen \(\displaystyle \underline x\) pénzfelvételt ezentúl nevezzük jónak.
Tekintsük most egy jó \(\displaystyle \underline x\) pénzfelvételhez tartozó összes lehetséges összeg \(\displaystyle A(\underline x)\) átlagát. Azaz
\(\displaystyle A(\underline x)=\frac1{n!}\sum_{(d_1,d_2,...,d_n)\in P}\sum_{i=1}^n \lambda_ix_i\)
Adott jó pénzfelvétel esetén adott i-re \(\displaystyle \lambda_i\) értéke akkor 1, ha \(\displaystyle d_i\in\{x_i,x_i+1000,...,1000n\}\). Ez \(\displaystyle \left(n-\frac{x_i}{1000}+1\right)\) eset és mindegyik eset (n-1)!-féleképpen állhat elő, ezért
\(\displaystyle A(x)=\frac1{n!}\sum_{i=1}^n(n-\frac{x_i}{1000}+1)(n-1)!x_i=\frac{1000}{n}\left((n+1)\sum_{i=1}^n\frac{x_i}{1000}-\sum_{i=1}^n{\left(\frac{x_i}{1000}\right)^2}\right)\).
Felhasználva a számtani és négyzetes közép közötti összefüggést
\(\displaystyle A(\underline x)\leq\frac{1000}{n}\left((n+1)\sum_{i=1}^n\frac{x_i}{1000}-\frac{\left({\sum_{i=1}^n\frac{x_i}{1000}}\right)^2}{n}\right)=\frac{1000}{n^2}\left(n(n+1)\sum_{i=1}^n\frac{x_i}{1000}-\left(\sum_{i=1}^n\frac{x_i}{1000}^2\right)\right)\)
Mivel tetszőleges a>0 számra az f(t)=t(a-t) függvényre \(\displaystyle f(t)\leq\frac{a^2}4\), ezért
\(\displaystyle A(\underline x)\leq\frac{1000}{n^2}\frac{n^2(n+1)^2}4=1000\frac{(n+1)^2}4\).
Mivel számok minimuma legfeljebb az átlaguk, ezért az összes jó pénzfelvételre teljesül:
\(\displaystyle m(\underline x)\leq A(\underline x)\leq 1000\frac{(n+1)^2}4\)
Ha most n páratlan, akkor \(\displaystyle \frac{n+1}2\) egész szám és könnyen látható, hogy az
\(\displaystyle \underline x=\left(1000\frac{n+1}2,...,1000\frac{n+1}2\right)\) pénzfelvétel esetén a felvett összeg éppen \(\displaystyle 1000\frac{(n+1)^2}4\), hiszen a fenti egyenlőtlenségek egyenlőséggel teljesülnek. Ezért ebben az esetben igaz az állítás.
Ha n páros, azaz n=2k, akkor a fentiek szerint minden jó pénzfelvételre
\(\displaystyle m(\underline x)\leq1000\frac{(2k+1)^2}4=1000k(k+1)+250\)
De jó pénzfelvétel esetén a kivett összeg osztható 1000-rel, ezért
\(\displaystyle m(\underline x)\leq1000k(k+1)\)
A fenti felső korlát viszont elérhető \(\displaystyle \underline x=(1000k,...,1000k)\) és \(\displaystyle \underline x=(1000(k+1),...,1000(k+1))\) esetén is és ekkor
\(\displaystyle m(\underline x)=1000k(k+1)=1000\left[\frac{(n+1)^2}4\right]\) is teljesül, tehát ekkor is igaz az állítás.
Esetünkben n páros, k=5, ezért legfeljebb 30000 dollár vehető ki.
|
| Előzmény: [41] Róka Sándor, 2024-07-14 22:22:50 |
|
| [58] Róka Sándor | 2024-07-19 19:15:58 |
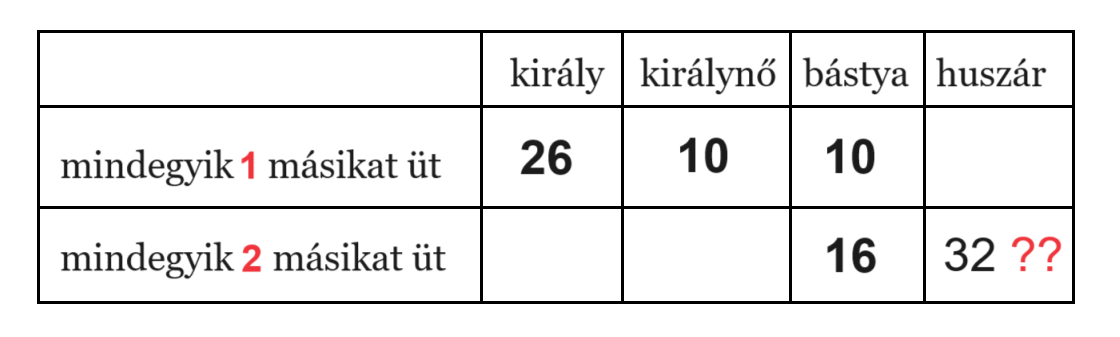
 A táblázat mutatja, hogy eddig milyen válaszokat találtunk. Ha megtaláljuk a válaszokat a 8–11. kérdésekre, azok a számok kerülnek majd az üres mezőkbe.
A táblázatban a 10-es számhoz tartozó bástyás feladat volt a KöMaL-ban, F.2296., illetve az Arany Dániel versenyen kezdőknek, tagozatos kategóriában az 1973-as döntőn.
|
 |
| Előzmény: [57] Róka Sándor, 2024-07-18 06:27:32 |
|
| [57] Róka Sándor | 2024-07-18 06:27:32 |
 Legfeljebb hány a) király; b) királynő helyezhető a táblára, hogy mindegyik legfeljebb egy másikat tartson ütés alatt?
Ez volt a 3., illetve 6. kérdés. A válaszok: 26 és 10.
Bástyára is kérdezhetjük, ez hasonló a királynős feladathoz, itt 10 a válasz.
Legfeljebb hány a) király; b) királynő; c) bástya helyezhető a táblára, hogy mindegyik pontosan két másikat tartson ütés alatt?
A c) kérdés volt Danka Emma kérdése (a 2. kérdés). A válasz: 16.
Mi lehet a válasz a)-ra és b)-re? (Nem ismerem a válaszokat.)
8. kérdés: Legfeljebb hány király helyezhető a táblára, hogy mindegyik pontosan két másikat tartson ütés alatt?
9. kérdés: Legfeljebb hány királynő helyezhető a táblára, hogy mindegyik pontosan két másikat tartson ütés alatt?
A Héttusa 29. feladatában megmutattuk, elhelyezhető a táblán 32 huszár úgy, hogy mndegyik pontosan két másikat tarson ütés alatt.
Adódik két kérdés:
10. kérdés: Legfeljebb hány huszár helyezhető a táblára, hogy mindegyik pontosan egy másikat tartson ütés alatt?
11. kérdés: Legfeljebb hány huszár helyezhető a táblára, hogy mindegyik pontosan két másikat tartson ütés alatt?
|
| Előzmény: [41] Róka Sándor, 2024-07-14 22:22:50 |
|
| [56] SmallPotato | 2024-07-17 22:17:25 |
 Rendben. Ha nem is leesett végre, de levánszorgott. :)
Mindenképpen a letámadott "cellák" darabszámával akartam operálni, dehát a FALdarab az nem cella.
Köszönöm a türelmet és a segítséget. :)
|
| Előzmény: [55] Róka Sándor, 2024-07-17 21:21:33 |
|
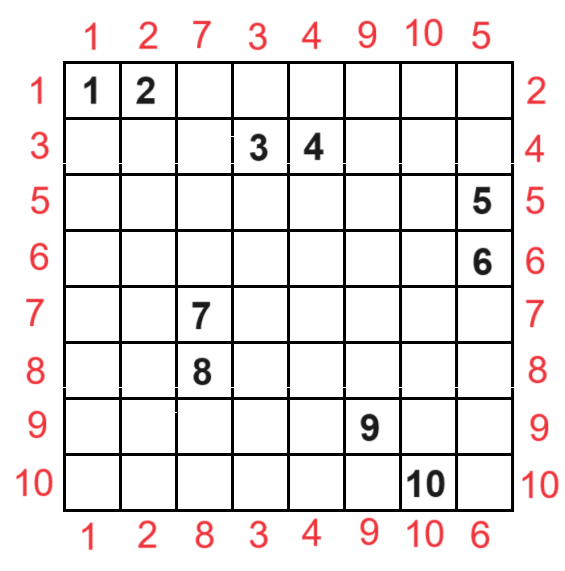
| [55] Róka Sándor | 2024-07-17 21:21:33 |
 Ez a jó szóhasználat, hogy a királynő 4 irányban néz, és adott esetben csak 3 irányban lát akadálytalanul. (53. hozzászólás, Káli gúla)
A 47. hozzászólásban lévő sakktáblát a 10 királynővel most úgy rajzoltam le, ami mutatja azt, hogy a 10 királynő mely faldarabokat látja. Például a fekete 1-es a piros 1-esekkel jelölt faldarabokat látja.
32 faldarab van. Az 1–8 bábuk 3–3 faldarabot látnak, a 9 és 10 bábu 4–4 faldarabot lát.
|
 |
| Előzmény: [54] SmallPotato, 2024-07-17 20:01:17 |
|
| [54] SmallPotato | 2024-07-17 20:01:17 |
 De ugyanazt a fal-elemet ketten is "láthatják" (a megoldásban látjuk is, hogy látják is), tehát a korlát nem a fal-elemek száma, hanem annak a duplája. És - nem mellékesen - váltig fenntartom, hogy az a 32 az 28. (Aminek megfelelően, szerintetek 3x <= 28 kellene, csakhogy az ábrás tények ennek ellentmondanak)
|
| Előzmény: [53] Káli gúla, 2024-07-17 18:52:20 |
|
| [53] Káli gúla | 2024-07-17 18:52:20 |
 Úgy érdemes elképzelni, hogy amikor 2 bábu vonalban van, akkor a falhoz közelebbi leárnyékolja a falszakaszt. Alternatív hasonlattal, a közelebbi "látja" abban a vonalban a falat, a távolabbi meg nem. Minden bábu négyfelé néz, de legalább három irányban akadálytalanul "lát" falat, összesen legfeljebb 32-t. \(\displaystyle 3x\le32\) miatt \(\displaystyle x\le10\).
|
| Előzmény: [52] SmallPotato, 2024-07-17 18:37:35 |
|
| [52] SmallPotato | 2024-07-17 18:37:35 |
 Még mindig nem értem (inkább: nem értek egyet).
Szerintem:
Faldarabból nem 32 van, hanem 28. Számold meg!
Egy faldarabra (csak a vízszintes és függőleges irányokat tekintve) természetesen nem csak egy, hanem két királynő is lőhet (az általad ábrán mellékelt megoldásban például minden faldarabon vagy áll egy királynő, vagy pontosan két királynő támadja).
Az érvelés ezek után olyasmire lenne alapozható, hogy 10 királynő esetén azok max. 10*3 = 30 faldarabot támadnak; a faldarabok száma ugyan csak 28, viszont mindegyik kétszer támadható, tehát a falak mentén legalább 2*28 = 56 támadási lehetőség van; a 10 királynő tehát ezen az alapon nem kizárt, hogy elhelyezhető.
A baj csak az, hogy ezen az alapon még a 11 sem kizárt.
Bocsánat az akadékoskodásért!
|
| Előzmény: [51] Róka Sándor, 2024-07-17 15:14:20 |
|
| [51] Róka Sándor | 2024-07-17 15:14:20 |
 Vázlatosan és pontatlanul fogalmaztam. Valóban nem a fal hosszát, hanem a faldarabok számát figyeljük. Ezekből a darabokból \(\displaystyle 4\cdot8=32\) van.
A bizonyításban (hogy max. 10 királynő lehet) a királynőnek csak azt a tulajdonságát használjuk, hogy vízszintes és függőleges irányban lő. Fontos, hogy kihagyjuk az átlós irányt. Emiatt mondhatjuk, hogy egy kiválasztott faldarabra a táblára helyezett királynők közül csak egy királynő tud lőni.
Egy a táblán lévő királynő 3 vagy 4 faldarabot lőhet, mert a négy lövésirányból max. csak az egyikben állhat akadályként egy másik királynő.
10 királynő még állhat a táblán, ha mindegyik 3 faldarabot lő, ekkor a 32 faldarabból 30-at kilőnek. Így még belefér az, hogy 2 királynő 4-4 faldarabot lő.
De 11 királynő esetén legalább \(\displaystyle 11\cdot3=33\) különböző faldarabot lőnek, ami nem megy, mert csak 32 faldarab van.
Így az következik, hogy legfeljebb 10 királynő állhat a táblán.
Bocs, hogy korábban elnagyoltan és szűkszavúan fogalmaztam.
|
| Előzmény: [50] SmallPotato, 2024-07-17 14:11:52 |
|
