Matematikából kitűzött gyakorlatok és feladatok
1998. március

Általános iskolások részére javasolt példák: C. 497., C. 500., Gy. 3190., Gy. 3191., Gy. 3192.

A pontversenyben kitűzött C gyakorlatok

C. 497. Van-e olyan n pozitív egész szám, amelyre 1^.2^.3^....^.(n-1)^.n, azaz n! pontosan 100 nullára végződik?

C. 498.Oldjuk meg a következő egyenlőtlenséget: x³+1>x²+x.

C. 499. Egy egységnyi sugarú kör körül úgy helyezkedik el n darab egyenlő sugarú kör a síkon, hogy mindegyikük kívülről érinti az egységkört és a ,,koszorúban'' lévő két szomszédját. Határozzuk meg a körök sugarát n függvényében. A sugarakat számítsuk is ki négy tizedesjegy pontossággal az n első négy lehetséges értékére.

C. 500. Be lehet-e csúsztatni egy 28 cm széles reklámtasakba két 22 cm széles művészeti albumot és egy 25 cm széles szakácskönyvet, ha mindhárom könyv külön-külön 1,5 cm vastag?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. április 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3190. A 49 szám két jegye közé beírjuk a 48 számot. Ezután a 4-es és a 8-as közé újra beírjuk a 48-at, majd ezt néhányszor megismételjük (44...48...89). Igaz-e, hogy így mindig négyzetszámot kapunk?

Gy. 3191. Igaz-e, hogy minden egész számnak legalább annyi pozitív 4k+1 alakú osztója van, mint 4k-1 alakú?

Gy. 3192. Keressük meg azokat a pozitív egész A, B számokat, amelyek tízes számrendszerbeli alakját egymás után írva négyzetszámot kapunk, és ez egyenlő az A és B szorzatának kétszeresével.

Gy. 3193. Egy kosár mogyorót n kupacba osztottunk szét. összekevertük, és utána n+k kupacot készítettünk belőlük (k>0). Bizonyítsuk be, hogy legalább k+1 szem mogyoró kisebb kupacba került, mint amekkorában előzőleg volt. (H)

Gy. 3194. Egy háromszög két magasságának hossza legalább akkora, mint a hozzájuk tartozó oldal. Mekkorák a háromszög szögei?

Gy. 3195. Egy derékszögű háromszögbe írt kör középpontján át mindegyik oldallal párhuzamost húzunk. A három egyenes a háromszög mindegyik oldalát három szakaszra osztja. Bizonyítsuk be, hogy az átfogón kapott középső szakasz hossza egyenlő a befogókon keletkezett középső szakaszok hosszának összegével.

Gy. 3196. A sík A pontjából kiinduló e₀, e₁, ..., e₆ félegyenesei közül e₁ az e₀-lal és minden következő az előzővel 30^o-os szöget zár be. Vetítsük merőlegesen az e₀ A-tól egységnyi távolságra lévő B₀ pontját az e₁-re, a vetület legyen B₁. Vetítsük hasonlóan B₁-et az e₂-re, a vetület legyen B₂ és így tovább. Számítsuk ki a B₀B₁...B₆ töröttvonal hosszát, és a B₀B₁...B₆ sokszög területét.

Gy. 3197. Egy vízszintes síkra négy, egymást érintő r sugarú gömböt helyezünk el úgy, hogy középpontjaik négyzetet alkossanak. A négy gömbre ráteszünk egy ötödik r sugarú gömböt, amelyik mind a négy másikat érinti. Milyen távolságra van a síktól az ötödik gömb legmagasabban lévő pontja? (H)

A pontversenyben kitűzött feladatok

F. 3220. Egy téglalap alakú mezőt az oldalaival párhuzamos egyenesek segítségével 100 db egybevágó téglalap alakú parcellára osztottunk úgy, hogy a szomszédos parcelláknak az egyik oldala közös. Kezdetben a mezőn 9 parcella gazos volt. Egy parcella elgazosodik, ha legalább két szomszédja gazos. Lehetséges-e, hogy előbb-utóbb az egész mező elgazosodik?

F. 3221. Az A₁A₂...A_n szabályos n-szög csúcsaira valamilyen sorrendben felírjuk az 1,2,...,n számokat.

a) Mekkora lehet legfeljebb a szomszédos számok közötti különbségek abszolút értékeinek összege?

b) Ez a maximális összeg hányféle elrendezésnél fordulhat elő?

F. 3222. Legyen n prímszám. Bizonyítsuk be, hogy ekkor az (1ⁿ+2ⁿ+...+xⁿ)+(1ⁿ+2ⁿ+...+(n-1)ⁿ)=1ⁿ+2ⁿ+...+(2n-1)ⁿ egyenletnek nincs pozitív egész megoldása.

F. 3223. Hány oldala lehet egy olyan sokszögnek, amelynek pontosan n darab szimmetriatengelye van?

F. 3224. Bizonyítsuk be, hogy ha egy konvex poliéder minden lapja középpontosan szimmetrikus, akkor legalább hat lapja paralelogramma.

Javasolta: Rudolf Gábor, Budapest

F. 3225. Adjunk meg a térben olyan ponthalmazt, amelynek bármely síkon van legalább egy, de legfeljebb öt pontja.

A pontversenyben kitűzött nehezebb feladatok

N. 167. Adott a síkon három egységnyi sugarú körlemez. Legyen t₁ és t₂ annak a két tartománynak a területe, amelyet a körök pontosan egyszer, illetve pontosan kétszer fednek le. Igazoljuk, hogy .

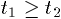N. 168. Igazoljuk, hogy tetszőleges n pozitív egész számra .

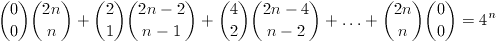N. 169. Jelölje a_n egy n résztvevős verseny lehetséges végeredményeinek számát, ha megengedjük a holtversenyt is; például a₂=3 és a₃=13. Bizonyítsuk be, hogy .

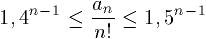N. 170. Bizonyítsuk be, hogy ha 15a+6b+4c+8d=0, akkor az ax³+bx²+cx+d=0 egyenletnek van pozitív gyöke.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. április 15.