Matematikából kitűzött gyakorlatok és feladatok
1998. szeptember

Kérjük beküldőinket, olvassák el a versenykiírást!

Általános iskolások részére javasolt példák: C. 509., C. 510., Gy. 3214., Gy. 3216., Gy. 3218., Gy. 3219.

A pontversenyben kitűzött C gyakorlatok

C. 509. Egy mozgólépcsőn 125 lépcsőfok van. Az egyenletesen felfelé haladó mozgólépcsőn mi is elindulunk felfelé, és 45 lépcsőfok megtétele után felérünk. Legközelebb már 55 lépcsőfokot tudunk ily módon megtenni. (A mozgólépcső sebessége nem változott.) Hányszorosára sikerült sebességünket növelni?

Javasolta: Fried Ervin, Budapest

C. 510. Legyen A tízmilliárd jegyű, kilenccel osztható pozitív szám. Az A számjegyeinek összege B, a B számjegyeinek összege C. Mekkora a C számjegyeinek összege?

C. 511. Egy paralelogramma oldalai 4 cm és 7 cm hosszúak; két átlójának hossza között pedig 2 cm a különbség. Mekkorák a paralelogramma átlói?

C. 512. A kör alakú torta negyedrésze (15 cm sugarú negyedkör) még megvolt, amikor elmentek a vendégek. Azután levágtunk a szélső sugarakkal párhuzamosan egy-egy 1,5 cm széles csíkot, és megettük. Hányadrészét fogyasztottuk el a tortadarabnak?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. október 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3214. Egy társaságban valakit ,,félénk''-nek hívunk, ha legfeljebb 3 ismerőse van. Bizonyítsuk be, hogy ha mindenkinek van legalább 3 félénk ismerőse, akkor mindenki félénk. Hányan lehetnek ekkor a társaságban?

Gy. 3215. Jelölje \(\displaystyle sigma" ALIGN=ABSCENTE\)(n) az n pozitív osztóinak összegét. (Például \(\displaystyle sigma" ALIGN=ABSCENTE\)(3)=1+3=4, \(\displaystyle sigma" ALIGN=ABSCENTE\)(6)=1+2+3+6=12.) Igaz-e, hogy ha \(\displaystyle sigma" ALIGN=ABSCENTE\)(n)>2n, akkor n minden m többszörösére teljesül a \(\displaystyle sigma" ALIGN=ABSCENTE\)(m)>2m egyenlőtlenség?

Gy. 3216. Milyen a, b esetén van közös megoldása a

19x²+19y²+ax+by+98=0

98x²+98y²+ax+by+19=0

egyenleteknek?

Gy. 3217. Melyek azok a p prímszámok, amelyekre a

p+1=2x²

p²+1=2y²

(Német versenyfeladat)

Gy. 3218. Az O középpontú kör két pontja A és B, egy O-tól különböző belső pontja P. Szerkesszünk a körön egy C és egy D pontot úgy, hogy a PAB és a PCD háromszög egyező körüljárású és hasonló legyen.

Bohner Géza (Cegléd) javaslata alapján

Gy. 3219. Az ABCD konvex érintőnégyszögbe írt r sugarú kör középpontját jelölje O. Bizonyítsuk be, hogy az OAB és OCD háromszögek köré írt körök közül valamelyiknek a sugara legalább r.

Gy. 3220. Egy húrtrapéz két párhuzamos oldala a és b (a<b). A hosszabbik alap egyik végpontjából a rövidebb alap 45^o-os szögben látszik. Mekkora lehet a trapéz területe?

Gy. 3221. Bizonyítsuk be, hogy hat egybevágó szabályos oktaéderből és nyolc velük egyező élű szabályos tetraéderből össze lehet rakni egy kétszer akkora élű szabályos oktaédert. (H)

A pontversenyben kitűzött feladatok

F. 3238. Bizonyítsuk be, hogy tetszőleges a, b, c valós számok esetén igaz a következő egyenlőtlenség:

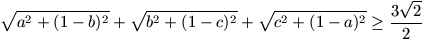
F. 3239. Mely x, y természetes számokra teljesül az x²(x²+y²)=y¹⁰⁰ egyenlőség?

F. 3240. Bizonyítsuk be, hogy végtelen sok olyan a, b pozitív egész számokból álló pár van, amelyre a osztója (b²+b+1)-nek, és b osztója (a²+a+1)-nek.

F. 3241. Az ABC háromszög AB, AC, illetve CB oldalán lévő C₁, B₁, A₁ pontokra

.

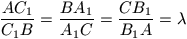Legyen az AC₁B₁, BC₁A₁, CA₁B₁, A₁B₁C₁ és ABC háromszögek beírt köreinek sugara rendre r₁, r₂, r₃, r₄ és r. Milyen \(\displaystyle lambda" ALIGN=ABSCENTE\) értékekre teljesül az

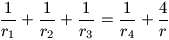
egyenlőség?

Javasolta: Bíró Bálint, Eger

F. 3242. Egy (zárt) K síkidom és egy P pont távolsága legyen a PQ távolságok minimuma, ahol \(\displaystyle Q eleme K-nak" ALIGN=ABSCENTE\). Adott a síkon egy négyzet és egy rajta kívül elhelyezkedő olyan kör, amelynek középpontja a négyzet egyik oldalegyenesén van. Határozzuk meg a síkon azon pontok halmazát, amelyek egyenlő távolságra vannak a körtől és a négyzettől.

F. 3243. Mutassuk meg, hogy ha a tér a, b, c, d páronként kitérő egyeneseire igaz, hogy a és b, valamint c és d normáltranszverzálisai is, és a és c, valamint b és d normáltranszverzálisai is merőlegesek egymásra, akkor a és d, valamint b és c normáltranszverzálisai is merőlegesek egymásra.

A pontversenyben kitűzött nehezebb feladatok

N. 179. Adott 3 kollineáris pont. Bizonyítsuk be, hogy minden pozitív egész n esetén megadható mindegyik pont körül n különböző sugarú kör úgy, hogy a sík azon pontjainak száma, amelyek 3 körvonalra illeszkednek, legalább cn², ahol c a pontok helyzetétől független pozitív állandó.

N. 180. Adott a síkon az ABCD trapéz, AC és BD átlóinak metszéspontja F. Az E pont úgy illeszkedik az AD szárra, hogy EF párhuzamos AB-vel. Adott két parabola, amelyeknek tengelyei párhuzamosak a trapéz alapjaival. Az egyik átmegy a B, C, E pontokon, a másik érinti az AD, BD, AC egyeneseket. Bizonyítsuk be, hogy a parabolák érintik egymást.

N. 181. Adott néhány gömb, amelyeknek van közös belső pontjuk. Ugyanezeket a gömböket elhelyezhetjük a térben másképp is úgy, hogy bármely kettő középpontja közti távolság csökkenjen. Igazoljuk, hogy a gömbök új helyzetében is van közös belső pontjuk.

N. 182. Határozzuk meg az összes olyan a, b pozitív egész számokból álló párt, amelyre a osztója (b²+b+1)-nek és b osztója (a²+a+1)-nek.

Javasolta: Fried Ervin, Budapest

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. október 15.