Matematikából kitűzött gyakorlatok és feladatok
1998. október

Általános iskolások részére javasolt példák: C. 513., C. 515., Gy. 3222., Gy. 3226., Gy. 3227.

A pontversenyben kitűzött C gyakorlatok

C. 513. Egy 25 méter hosszú feltekercselt vezetéket 2 és 3 méteres darabokra vágunk fel. Hányféleképpen tehetjük ezt meg, ha a különböző méretű darabok sorrendje is számít?

C. 514. Jelölje S_n a (2ⁿ, 2ⁿ⁺¹) intervallumba eső egész számok összegét. Bizonyítsuk be, hogy S_n minden pozitív egész n szám esetén osztható 3-mal. Milyen pozitív egész n-ekre osztható S_n 9-cel?

C. 515. Egy kockát felosztottunk 27 egybevágó kis kockára. Legfeljebb hány kis kockát döfhet át egy egyenes?

C. 516. Igazoljuk, hogy minden tetraédernek van olyan magassága, amely legalább akkora, mint a tetraéderbe írható gömb átmérőjének kétszerese.

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. november 16.

A pontversenyben kitűzött gyakorlatok

Gy. 3222. Legyenek A és B 9-jegyű számok. Tegyük fel, hogy A bármelyik számjegyét B-nek megfelelő (ugyanolyan helyiértéken álló) számjegyével helyettesítve 7-tel osztható számot kapunk. Mutassuk meg, hogy akkor ez megfordítva is teljesül, azaz B egy tetszőleges számjegyét A megfelelő jegyével helyettesítve, ugyancsak 7-tel osztható számot kapunk.

Gy. 3223. Legyenek x, y, z pozitív valós számok. Igaz-e, hogy

a) ha 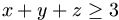, akkor ?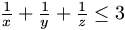

b) ha 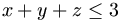, akkor ?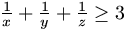

Angol versenyfeladat

Gy. 3224. Oldjuk meg a következő egyenletrendszert a pozitív egészek körében:

Gy. 3225. Az (a_i) sorozatot a következőképpen definiáljuk: a₁=1, 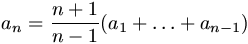. Határozzuk meg a₁₉₉₈ értékét.

Gy. 3226. A k₁ és k₂ körök közös pontjai A és B. A k₁ kör A pontbeli érintője k₂-t a C pontban, a k₂ B pontbeli érintője a k₁ kört a D pontban metszi. Bizonyítsuk be, hogy BD^2.BC=AC^2.AD.

Gy. 3227. Egy körbe két alakzatot írunk. Egy trapézt, amely a kör egyik átmérőjén nyugszik, és egy egyenlő szárú háromszöget, amelynek szárai párhuzamosak a trapéz száraival. Bizonyítsuk be, hogy a két alakzat területe egyenlő.

Gy. 3228. Egy húrnégyszög oldalai rendre 2, 3, 4, 6 egységnyiek. Milyen arányban osztják egymást az átlók?

Bodó Boglárka (Budapest) javaslata alapján

Gy. 3229. Bizonyítsuk be, hogy egybevágó szabályos tetraéderekkel, és velük egyező élű szabályos oktaéderekkel a tér hézag és átfedés nélkül kitölthető. (H)

A pontversenyben kitűzött feladatok

F. 3244. Határozzuk meg az összes pozitív x számot, amely megoldása valamely 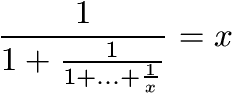alakú egyenletnek.

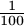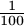F. 3245. Egy mókus mogyorót gyűjtött télire. Első nap megevett 1 szemet és a maradék -ad részét, a másodikon 2 szemet és a maradék -ad részét, és így tovább. Végül az utolsó, n-edik napon megette a megmaradt n mogyorót. Hány szem mogyorót gyűjtött a mókus?

F. 3246. Legyen x₁ pozitív, 1-nél kisebb szám. Ebből kiindulva képezzük az 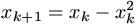előírással meghatározott sorozatot. Mutassuk meg, hogy n bármekkora, .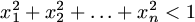

F. 3247. Az ABCD négyszög A-ból induló oldalainak mértani közepét A-ból felmérve az AB és az AD félegyenesekre, kapjuk a K és az L pontokat, a C-ből induló oldalainak mértani közepét C-ből felmérve a CB és a CD félegyenesekre pedig az M és az N pontokat. Milyen feltétel mellett teljesül, hogy KL=MN?

F. 3248. Egy 5 lányból és 5 fiúból álló társaság azonos nemű tagjai nem ismerik egymást, továbbá nincs két olyan lány, akinek lenne két közös fiúismerőse. Legfeljebb hány ismeretség van a társaság tagjai között? Hogyan módosul a válasz, ha a társaságban 7 lány és 7 fiú van?

F. 3249. Egy konvex poliéder minden lapja páratlan oldalú sokszög, és minden csúcsában páratlan sok él találkozik. Lehetséges-e, hogy a háromszöglapok számának és a három élre illeszkedő csúcsok számának az összege 9?

A pontversenyben kitűzött nehezebb feladatok

N. 183. Az y=x² egyenletű parabolát ,,csúszásmentesen elgurítjuk'' az x tengelyen. Milyen messzire távolodhat el a parabola az y tengelytől?

N. 184. Egy végtelen fagráf minden éle két olyan rácspontot köt össze, amelyek távolsága legfeljebb 1998. A sík minden rácspontja csúcsa a gráfnak. Bizonyítsuk be, hogy van két egységnyi távolságra lévő pont a síkon, amelyeket a fagráfban legalább 10¹⁹⁹⁸ hosszúságú út köt össze.

N. 185. Adjunk meg olyan, az egész számokon értelmezett többváltozós, egész együtthatós polinomot, amelynek értékkészlete bizonyos negatív számokból és az 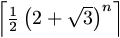(n=1,2,...) alakú számokból áll.

N. 186. Igaz-e, hogy ha valamely x valós számra és n pozitív egészre cos nx és cos (n+1)x racionális, akkor cos x is racionális?

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. november 16.