Az 1999. szeptemberi számban kitűzött A-jelű matematika feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 215. A P, Q és R pontok úgy helyezkednek el az O középpontú 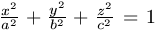egyenletű ellipszoidon, hogy az OP, OQ, OR szakaszok páronként merőlegesek egymásra. Mutassuk meg, hogy a PQR sík és O távolsága nem függ P, Q, és R megválasztásától.

Jugoszláv versenyfeladat

Megoldásvázlat. Legyen a három koordináta-egységvektor e₁, e₂, e₃, ezen kívül OP=d₁, 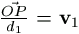, OQ=d₂, 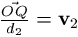, OR=d₃, 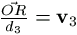. Végül legyen u_ij=e_iv_j (i,j=1,2,3).

Legyen T az origó vetülete a PQR síkra. Könnyen látható, hogy 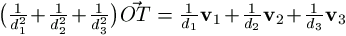, és 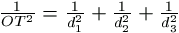. Azt kell tehát igazolni, hogy az utóbbi összeg állandó.

A feltételek szerint a v₁, v₂, v₃ vektorok egységnyi hosszúak és páronként merőlegesek. Ebből következik, hogy tetszőleges i-re

u_i1²+u_i2²+u_i3²=|e_i|²=1.   (1)

Az ellipszoid egyenletébe behelyettesítve P, Q, R koordinátáit, azaz a (d_ju_1j,d_ju_2j,d_ju_3j) számhármasokat,

,

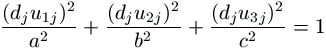azaz

.

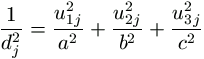Ezeket összegezve j értékeire,

= = .

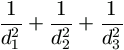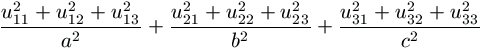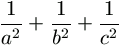Megjegyzés. A megoldás szó szerint ugyanígy megy akárhány dimenzióban.

A. 216. Bizonyítsuk be, hogy tetszőleges n pozitív egészhez létezik olyan legfeljebb n-edfokú, egész együtthatós p polinom, hogy páros x egész szám esetén p(x) osztható 2ⁿ-nel, páratlan x esetén pedig p(x)-1 osztható 2ⁿ-nel.

Javasolta: Hajnal Péter, Szeged

Megoldásvázlat.

1. lemma. Elég, ha a feltétel a p(0), p(1), ..., p(n) számokra teljesül, ebből már következik az összes többi egész számra.

Bizonyítás. Ismeretes, hogy ha a p polinom foka kisebb, mint m, akkor

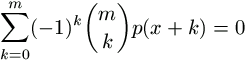.   (1)

Ezt mi természetesen az m=n+1 választással fogjuk használni.

Legyen r(x)=0 ha x páros, és legyen r(x)=1 ha x páratlan. Ha p helyett ezt a függvényt írjuk (1) baloldalára, akkor x paritásától függően 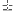2ⁿ-t kapunk, mert a páros illetve páratlan indexű binomiális együtthatók összege 2ⁿ.

Tegyük fel, hogy p(x-1), p(x-2), ..., p(x-n-1) a megfelelő maradékot adja 2ⁿ-nel osztva. Ekkor

,

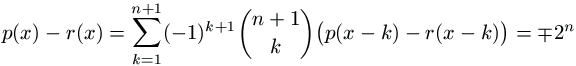a jobboldalon minden tag osztható 2ⁿ-nel, tehát p(x)r(x) mod 2ⁿ, vagyis p(x) maradéka is jó. Hasonlóan kapjuk, hogy p(x-n-2) maradéka is megfelelő. A 0, 1, ..., n számokból kiindulva, ilyen lépésekkel bármelyik egész számhoz eljuthatunk.

2. lemma. Tetszőleges 0<n, 0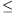k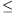n egész számokra, a k!(n-k)! szám prímtényezős felbontrásában a 2 kitevője legfeljebb n-1.

Biz. A k!(n-k)! szám osztója az n!-nak (a hányadosuk , a Legendre formula szerint a 2 kitevője az n!-ban

.

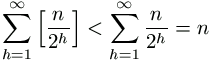Most teljes indukcióval igazoljuk a megfelelő p polinom létezését. Tegyük fel, hogy a q polinom megfelelő n helyett (n-1)-gyel. Ebből konstruáljuk p-t a következő alakban:

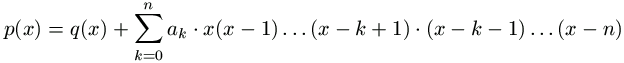,   (2)

ahol a₀, ..., a_n alkalmas egész számok.

Az 1. lemma alapján az a₀, ..., a_n számokat úgy kell megválasztani, hogy 0kn esetén p(k) r(k) mod 2ⁿ teljesüljön. (2) alapján

p(k)=q(k)+(-1)^n-kk!(n-k)!^.a_k.

Az indukciós feltevés szerint q(k)r(k) mod 2^n-1, a 2. lemma szerint k!(n-k)!-ban a 2 kitevője legfeljebb n-1, ezért az a_k biztosan megválasztható a kívánt módon.

Megjegyzés. Speciális n-ekre közvetlenül is lehet megfelelő polinomot konstruálni. Könnyen látható, hogy x^2mr(x) mod 2^m+1 tetszőleges x egész szám esetén, ugyanakkor az (x+1)(x+2)...(x+2^m) polinom értéke minden egész helyen osztható 2^2m-1-nel. Mindezekből következik, hogy ha az x^22m polinomot elosztjuk az (x+1)(x+2)...(x+2^m) polinommal, akkor a maradékul kapott polinom megfelelő lesz n=(2^m-1)-re.

A. 217. Az a₁, a₂, ..., a_n pozitív egészek legnagyobb közös osztója 1, és közülük bármelyik kettőnek ugyanaz a legkisebb közös többszöröse. Bizonyítsuk be, hogy létezik egy olyan p egész szám, hogy tetszőleges u egész szám esetén u és p-u közül pontosan az egyik írható fel a₁x₁+a₂x₂+...+a_nx_n alakban, alkalmas x₁, ..., x_n nemnegatív egészekkel.

Megoldásvázlat.

Mint könnyen ellenőrizhető, az a₁,..., a_n számokra vonatkozó feltétel azzal ekvivalens, hogy megfelelő, páronkét relatív prím b₁,..., b_n pozitív egészekkel a_i=b₁...b_i-1b_i+1...b_n.

Bebizonyítjuk, hogy a feladat állításának megfelelő szám

p=(n-1)b₁b₂...b_n-a₁-...-a_n.    (1)

Legyen u tetszőleges egész szám, és tegyük fel, hogy felírható a kívánt alakban:

a₁x₁+...+a_nx_n=u.

Vizsgáljuk ezt az egyenletet modulo b_i. A baloldalon a_i kivételével az összes együttható osztható a_i-vel, ezért

a_ix_i=(b₁...b_i-1b_i+1...b_n)x_iu mod b_i.

Legyen 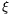_i(u) a legkisebb olyan nemnegatív egész, amelyre

(b₁...b_i-1b_i+1...b_n)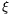 _i(u) u mod b_i.

Az előbbiek alapján, figyelembe véve, hogy b_i relatív prím (b₁...b_i-1b_i+1...b_n)-nel,

x_i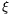i(u) mod b_i,

másrészt, 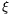_i(u) minimalitása miatt x_i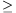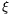i(u). Bevezetve tehát az 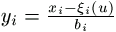jelölést,

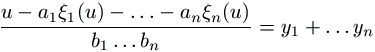
egy nemnegatív egész szám.

Vezessük be a

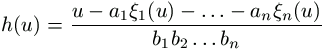   (2)

függvényt. Eddig azt láttuk, hogy ha u előállítható, akkor h(u) egy nemnegatív egész szám. Az is biztos, hogy h(u) mindig egész, mert (2) számálójában tetszőleges i-re u-a_i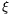i(u) osztható b_i-vel, a maradék tagokban pedig az a_j együttható osztható vele. Ha a h(u) egész szám nemnegatív, akkor u egy megfelelő előállítását kapjuk az x₁=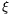₁(u)+h(u), x₂=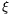₂(u), ..., x_n=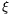_n(u) számokkal.

Ezzel bebizonyítottuk, hogy u akkor és csak akkor állítható elő, ha h(u)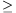0.

Vizsgáljuk most az u és p-u számokat. Tetszőleges i-re

a_i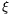i(u)+a_i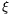i(p-u)p-a_i mod b_i,

amiből

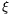_i(u)+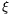_i(p-u)-1 mod b_i.   (3)

Mivel 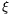_i értéke mindig 0 és b_i-1 közé esik, (3) csak úgy teljesülhet, ha 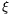_i(u)+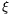_i(p-u)=b_i-1. Ezt beírva h(u)-ba és h(p-u)-ba,

h(u)+h(p-u)=u-a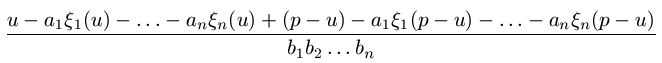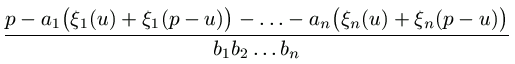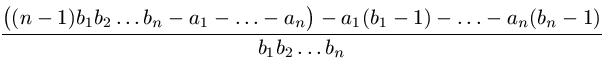₁ = = = = -1.

Ebből következik, hogy a h(u) és h(p-u) egész számok közül pontosan az egyik nemnegatív, azaz u és p-u közül pontosan az egyik állítható elő.