Matematikából kitűzött gyakorlatok és feladatok
1999. december

Figyelem! A pontverseny feltételei a tavalyi évhez képest megváltoztak. Kérjük, olvassa el a versenykiírást!

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 560. Egy cipó 25%-kal kisebb tömegű, mint egy fehér kenyér, ráadásul 20%-kal drágább. Igaz viszont, hogy a cipó az utolsó morzsáig elfogy, míg a kenyér 15%-a mindig ránkszárad. Ugyanakkora fogyasztást feltételezve hány százalékkal költünk többet, ha cipót veszünk, mint ha kenyeret?

C. 561. Keressük meg azokat a p prímeket, amelyekre a p²+11 számnak pontosan 6 pozitív osztója van.

C. 562. Keressük meg azt a pozitív egész n számot, amelyre

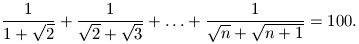
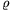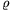C. 563. Egy O középpontú, r sugarú körben az átmérőnél kisebb húr legyen AB, az AO és BO sugarak által meghatározott kisebb körcikkbe beírt kör sugara pedig . Adjuk meg AB-t r és segítségével.

C. 564. Egy téglatest oldalélei 26, 20 és 8 egység hosszúak. A 26x8-as lapok fölé építsünk olyan egyenes sátortetőket, amelyek ,,ferde'' éleinek hossza 13, ,,vízszintes'' éle pedig 20 egység. Mekkora a téglatest azon részének térfogata, amelyet úgy kapunk, hogy eltávolítjuk a téglából a sátortetőknek a téglatesthez illeszkedő lapjukra vonatkozó tükörképeit?

A B pontversenyben kitűzött feladatok

B. 3322. Legfeljebb hány részre osztja a teret 4 olyan sík, amely egy ponton halad át? (3 pont)

B. 3323. Keressük meg azt a legbővebb intervallumot, amelyben 19/99 a legkisebb nevezőjű tört. (5 pont)

B. 3324. Hányféleképpen írható fel 1999¹⁹⁹⁹ egymás után következő természetes számok összegeként? (4 pont)

Javasolta: Káspári Tamás, Paks

B. 3325. A p₁, p₂, p₃, p₄ prímszámokat négyesikreknek nevezzük akkor, ha p₁<p₂<p₃<p₄, és p₄-p₁=8. Bizonyítsuk be, hogy ha a p₁, p₂, p₃, p₄ és a q₁, q₂, q₃, q₄ prímszámok is négyesikrek, továbbá p₁ és q₁ nagyobbak 5-nél, akkor p₁-q₁ osztható 30-cal, de nem lehet 60. (3 pont)

B. 3326. Egy szabályos oktaéder egyik lapját merőlegesen vetítjük a szemközti lap síkjára. A szemközti lap területének hányadrészét fedi le a vetület?

(4 pont)

Javasolta: Juhász Máté 8. o.t., Budapest

B. 3327. Adjunk meg egy egész együtthatós polinomot, amelynek a cos 18^o zérushelye! (4 pont)

B. 3328. Egy konvex sokszög minden oldalegyenesét az oldalra merőleges irányban kifelé eltoltuk 5 cm-rel. Mutassuk meg, hogy az így kapott sokszög kerülete több, mint 30 cm-rel nagyobb az eredeti sokszög kerületénél. (3 pont)

Javasolta: Magyar Zsolt, Budapest

B. 3329. Egy 31 fős osztályban a szokásos módon akarják egymást karácsonykor megajándékozni a gyerekek: december elején az egyik osztályfőnöki órán egy kalapba beleteszik a 31 nevet, és sorban mindenki kihúzza annak a nevét, akinek ajándékot készít. Mennyi a valószínűsége annak, hogy a húzást meg kell ismételni, mert valaki a saját nevét húzta? (4 pont)

B. 3330. Egy 105 egység oldalú négyzet belsejében 1999 egységnégyzetet helyeztünk el. Mutassuk meg, hogy elhelyezhető még egy egységnégyzet úgy, hogy ne legyen a többivel közös pontja. (5 pont)

B. 3331. A 12.b osztályba ugyanannyi fiú jár, mint lány, így a szalagavatón mindenkinek lesz az osztályból táncpartnere. A párok összeállításához minden fiú rangsorolja az összes lányt, és fordítva. Mutassuk meg, hogy párba állíthatók úgy, hogy ne legyen olyan fiú és lány, akik mindketten szívesebben táncoltak volna egymással, mint a nekik jutó partnerrel. (5 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 224. Bizonyítsuk be, hogy tetszőleges pozitív a₁, a₂, ..., a_n számokra

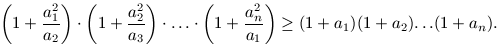
A. 225. Jelölje S₁ és S₂ az 1, 2, ..., n számok páratlan, illetve páros osztói számának összegét. Igazoljuk, hogy

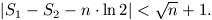
A. 226. Adott egy gráf, amelynek csúcsai a pozitív egész számok és nem tartalmaz kxk-as teljes páros részgráfot. (k egy rögzített pozitív egész.) Igazoljuk, hogy létezik tetszőlegesen hosszú számtani sorozat, amelynek semelyik két eleme között nincs él.

Javasolta: Solymosi József, Budapest

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. január 15.