Fizikából kitűzött gyakorlatok és feladatok 2000. április

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

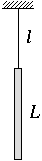M. 215. Egy L hosszúságú homogén rudat l hosszú fonálon felfüggesztünk. Mérjük meg a rendszer két sajátfrekvenciáját különböző l és L esetén! (Csak síkmozgásokat vizsgáljunk!)

Gnädig Péter, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3334. Tibor egy bizonyos útvonalon állandó sebességgel szokott kerékpározni. Egy alkalommal ennek az útvonalnak első x százalékát szokásos sebességénél éppen x százalékkal kisebb sebességgel tette meg. Az útvonal hátralevő szakaszán szokásos sebességének kétszeresével haladt, és így éppen a szokott időben ért célba. A teljes útnak hány százalékát tette meg a szokásosnál kisebb sebességgel? (3 pont)

Takács Gábor, Budapest

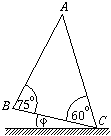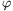P. 3335. Az ábrán látható ABC háromszög A csúcsából az AB és az AC oldalakon súrlódás nélkül csúszhatnak le pontszerű testek. Mekkora legyen az ábrán látható szög, hogy az A pontból kezdősebesség nélkül, egyszerre elengedett testek egyszerre érkezzenek a B, illetve C pontokba? (4 pont)

Varga István, Békéscsaba

P. 3336. A dízel-motorban a gázt adiabatikusan összenyomják. Ha a kezdeti hőmérséklet 27 ^oC, az összenyomás utáni hőmérséklet 681 ^oC lesz. Tegyük fel, hogy a gáz kétatomos molekulákból álló ideális gáznak tekinthető. Mekkora a kezdeti és az összenyomás utáni térfogat aránya (a sűrítési viszony, más néven kompresszió)? (4 pont)

Radnóti Katalin, Budapest

P. 3337.Egy vízszintes felületen nyugvó, gömb alakúnak tekintett higanycsepp energiája az alábbi formulával adható meg: E=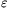V+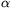A+mgr (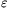>0 állandó, 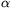a higany felületi feszültsége, r a csepp sugara, A a felszíne, V a térfogata, m pedig a tömege). Mekkora sugarú higanycseppnek van a legkisebb fajlagos (tömegegységre jutó) energiája? Határozzuk meg a sugarat numerikusan is! (4 pont)

Kiss Miklós, Gyöngyös

P. 3338. Az ábrán látható, egyik végén beforrasztott, A keresztmetszetű cső függőleges síkban helyezkedik el. A cső vízszintes részében levő L hosszúságú higanyoszlop L hosszúságú oxigéngázt zár el. A külső légnyomás L magasságú higanyoszlop hidrosztatikai nyomásával azonos.

A cső környezetében a hőmérséklet lassan emelkedik. Mekkora a gáz térfogata akkor, amikor a gáz által végzett munka a felvett hő 20 %-a? (A függőleges szár elegendően hosszú.) (5 pont)

Kotek László, Pécs

P. 3339.Két R sugarú fémgömböt helyezünk el egymástól r távolságra (r>>R). Az egyiknek Q₁, a másiknak Q₂ töltése van. Legfeljebb mennyi energia fordítódik annak a huzalnak a melegítésére, amellyel a két fémgömböt összekötjük?

Adatok: Q₁=3^.10^-8 C, Q₂=2^.10^-9 C, r=2 m, R=2 cm. (5 pont)

Légrádi Imre, Sopron

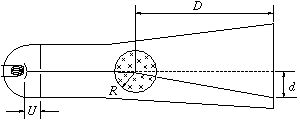P. 3340. Katódsugárcsőben egy tekercs segítségével R=2 cm sugarú, kör keresztmetszetű, homogén mágneses mezőt hoztunk létre. Amikor a tekercset bekapcsoljuk, az U=250 V feszültséggel felgyorsított elektronnyaláb eltérése a tekercs tengelyétől D=20 cm távolságban levő ernyőn d=10 cm. Mekkora az eltérítő mágneses mező indukciója? (A tekercs bekapcsolása előtt a nyaláb áthaladt a tekercs tengelyén.) (4 pont)

Holics László, Budapest

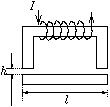P. 3341. Egy elektromágnes U alakú vasmagjának keresztmetszete A, középvonalának hossza L. A záró vasmag l hosszú és szintén A keresztmetszetű. Amikor a záró vasmag h távolságra van az U alakú vasmagtól, amelyen lévő tekercsben I áram folyik, a záró vasmagot F erővel húzza magához az elektromágnes. A vas permeabilitása nem állandó, de a mágneses indukciótól való 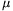(B) függését ismerjük.)

a) Hány menetből áll a tekercs?

b) Mekkora erővel szorítja magához az elektromágnes a záró vasmagot, ha nincs közöttük légrés? Mekkora ekkor a mágneses indukció és a relatív permeabilitás értéke a vasban?

Adatok: L=30 cm, l=12 cm, A=10 cm², h=1 mm, I=1 A, F=500 N, és 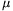(B)=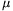₀(4500-2500 T^-1 B) a vizsgált tartományban. (5 pont)

Radnai Gyula, Budapest

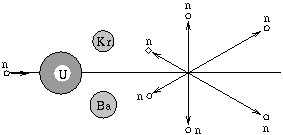P. 3342. Az ²³⁸U atommag gyors neutron lövedék hatására bekövetkező hasadásakor a következő magreakció jöhet létre:

.

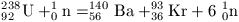Tételezzük fel, hogy a hasadási folyamat az ábrán látható módon játszódik le, és fennállnak az alábbiak:

a) a beérkező gyors neutron mozgási energiája 3,2^.10^-13 J;

b) a keletkező 6 neutron egy síkban, a beérkező neutron mozgásirányára szimmetrikusan, egymással 60^o-60^o-os szöget bezárva repül szét;

c) a felszabaduló magenergia 2,88^.10^-11 J;

d) a merőlegesen szétrepülő és a ,,hátrafelé'' repülő neutronok mozgási energiája azonos: 1,6^.10^-13 J;

e) a keletkező Kr és Ba hasadvány magok is merőlegesen repülnek szét.

Mekkora külön-külön a hasadványok mozgási energiája? (5 pont)

Tolna megyei Szilárd Leó fizikaverseny

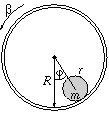P. 3343. Egy R belső sugarú, rögzített tengelyű csövet kicsiny 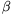szöggyorsulással kezdünk mozgatni.

A cső belsejébe egy tömör, homogén anyageloszlású, m tömegű, r sugarú rudat helyeztünk. (A súrlódás olyan nagy, hogy a rúd mindvégig tisztán gördül a csőben.)

a) Mekkora legyen az ábrán látható 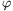szög, hogy a rúd tengelye helyben maradjon?

b) Hogyan mozog a rúd, ha induláskor a cső alján állt? (6 pont)

Balogh Péter, Budapest

Áprilisi pótfeladat (Beküldhető, de az eredménye nem számít bele a pontversenybe.) Becsüljük meg, mennyivel változna meg a nap hossza, ha 2000. április elsején éjfélkor az egész világon mindenhol áttérnének a jobb oldali közlekedésre!

K. F. Riley, Cambridge feladata nyomán

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. május 11.