A 2000. májusi B-jelű matematika feladatok megoldása

Bizonyos feladatoknál csak a megoldás vázlatát, esetleg a végeredményt közöljük.

B. 3372. Egy derékszögű háromszögről tudjuk, hogy a súlyvonalaiból mint oldalakból szerkesztett háromszög is derékszögű. Bizonyítsuk be, hogy a két háromszög hasonló. (3 pont)

Javasolta: Gyanta Nándor, Budapest

Megoldásvázlat. Használjuk az ábra jelöléseit!

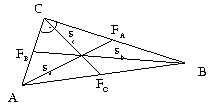
Pitagorasz tételét felírva az AF_AC és a BF_BC háromszögekre s_a²=a²/4+b², s_b²=a²+b²/4, s_c²=AF_C²=c²/4=(a²+b²)/4. Legyen c>a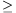 b. Ekkor s_b 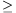s_a>s_c, tehát a súlyvonalakból szerkesztett derékszögű háromszögben a derékszög s_b-vel szemközt van, s így s_b²=s_a²+s_c², azaz a²+b²/4=a²/4+b²+c²/4, amiből a²=2b², tehát a/b= 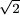. A hasonlósághoz elég lenne bizonyítani, hogy a/b=s_a/s_c. Valóban,

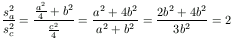
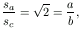
tehát a két háromszög valóban hasonló.

B. 3373. Az f egyenes két oldalán, tőle egységnyi távolságra megrajzoljuk az e és g egyeneseket. Legyenek E, F és G a megfelelő egyenesek megfelelő pontjai úgy, hogy az általuk meghatározott háromszögben F-nél derékszög van. Mekkora a háromszög F-ből induló magassága? (3 pont)

Javasolta: Pap Gyula, Debrecen

Megoldásvázlat. A példa a következő ötletből keletkezett: Vegyünk egy papírcsíkot. Hajtsuk be az egyik oldalát tetszőleges szögben, majd hajtsuk mellé a másik oldalát úgy, hogy a papírcsík szélei egymáshoz illeszkedjenek. A keletkező derékszögű háromszög magassága a papírcsík szélességével lesz egyenlő. Tehát a példában a háromszög magassága egységnyi.

B. 3374. Egy vizsga két részből áll, írásbeliből és szóbeliből. Mindkét részre 0-tól 9-ig terjedő egész értékű pontszámot lehet szerezni. A rangsorban A megelőzi B-t, ha A eredménye egyik vizsgán sem rosszabb, mint B-é, továbbá legalább az egyik vizsgán A eredménye határozottan jobb. Egy csoport húsz diákja közül semelyik kettő eredménye nem azonos. Bizonyítsuk be, hogy van a csoportban három diák, A, B és C, akik közül A megelőzi B-t és B megelőzi C-t. (4 pont)

Megoldásvázlat. Ha van három olyan tanuló, akik az egyik vizsgán azonos pontszámot értek el, akkor a másik vizsgán elért pontszámuk alapján rangsoroljuk őket: a legkisebb pontszámot elért legyen C, a következő B, a legnagyobb pedig A, s így teljesítik a feladat feltételeit. Ha nincs három ilyen diák, az azt jelenti, hogy mindkét vizsgán mindegyik pontszámot legfeljebb kétszer osztották ki. Ez legfeljebb 2^.10=20 tanulót jelent. Mivel a csoportban pont 20 diák van, ez azt jelenti, hogy mindkét vizsgán minden pontszámot pontosan kétszer osztottak ki. Válasszuk ki azt a két diákot, akik az írásbeli vizsgán 0 pontot értek el. Közülük az, aki a szóbelin több pontot ért el, lesz B, a másik pedig C. Az a diák lesz A, aki a szóbeli vizsgán B-vel azonos pontszámot kapott (az írásbelin biztosan 0-nál több pontot adtak neki). Ők hárman teljesítik a feltételeket, így a feladatot bebizonyítottuk.

B. 3375. Van-e olyan p(x)=x²+ax+b egész együtthatós polinom, amelyre a²-4b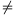0 és p(x) legalább 2000 egész helyen vesz fel négyzetszám értéket? (4 pont)

Megoldásvázlat. Létezik ilyen polinom, pl. p(x)=x²+2⁴⁰⁰² ilyen. Valóban, ha 1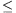 k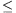 2000 és k egész, akkor

p(2^2000+k-2^2000-k)=(2^2000+k-2^2000-k)²+2⁴⁰⁰²=(2^4000+2k+2^4000-2k-2^.2⁴⁰⁰⁰)+2⁴⁰⁰²=2^4000+2k+2^4000-2k+2^.2⁴⁰⁰⁰=(2^2000+k+2^2000-k)²

és k felsorolt értékei mellett a 2^2000+k-2^2000-k egészek valamennyien különbözők.

B. 3376. Az ABC háromszög AC oldala egységnyi. Az A csúcsból induló súlyvonal 1:2 arányban osztja az A-nál lévő szöget. Mekkora lehet a háromszög AB oldala? (3 pont)

Javasolta: Mihalovics Sándor, Esztergom

Megoldásvázlat. Két eset van:

1. eset

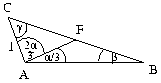
Felírva a szinusztételt az ACF ill. az ABF háromszögekre:

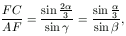amiből

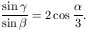
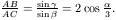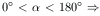
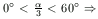
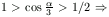
Most írjuk föl a szinusztételt az ABC háromszögre: AB= Mivel 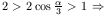1<AB<2.

2. eset

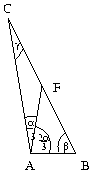
Az elsőhöz hasonlóan

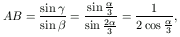tehát 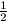<AB<1.

Összefoglalva: Az AB oldal hossza 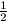és 2 között lehet, de nem lehet 1.

B. 3377. Legyen k páratlan szám. Mit ad maradékul a 2^n-1k²+2^n-2k⁴+2^n-3k⁸+...+2k^{2^n-1}+k^2ⁿ összeg 2ⁿ⁺²-nel osztva? (4 pont)

Javasolta: Bencze Mihály, Brassó

Megoldásvázlat. Megmutatjuk, hogy 2^n-i^.k^2ⁱ ugyanannyi maradékot ad 2ⁿ⁺²-nel osztva, mint 2^n-i, ha i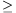 1 és k páratlan. Ehhez azt kell bizonyítani, hogy 2ⁿ⁺²|2^n-i(k^2ⁱ-1), azaz 2ⁱ⁺²|k^2ⁱ-1. Ezt i-re vonatkozó teljes indukcióval tesszük meg. Egy páratlan szám nyolccal osztva 1, 3, 5 vagy 7 maradékot ad, s így a négyzete 1-et. Így 8|k²-1, azaz az állítás i=1 esetén igaz. Tegyük föl, hogy l-ig igaz, hogy 2^l+2|k^{2^l}-1. Mivel k páratlan, ezért 2|k^{2^l}+1 és így 2^l+3|(k^{2^l}-1)k^{2^l}+1)=k^{2^l+1}-1. Tehát az állítás l+1-re is teljesül, ezzel az indukciót befejeztük. Vagyis 2^n-1k²+2^n-2k⁴+2^n-3k⁸+...+k^2ⁿ ugyanannyi maradékot ad 2ⁿ⁺²-nel osztva, mint 2^n-1+2^n-2+...+1=2ⁿ-1. Tehát a kifejezés 2ⁿ⁺²-nel osztva 2ⁿ-1-et ad maradékul.

Csikvári Péter dolgozata alapján

B. 3378. Egy érettségiző osztályban öt egyetemre felvételiznek, mindegyikre a diákoknak legalább a fele. Bizonyítsuk be, hogy van két olyan egyetem, hogy a diákoknak legalább az egyötöde mindkettőre jelentkezik. (5 pont)

Megoldásvázlat. Az osztály tanulóinak n elemű H halmazán értelmezzük az f_i:H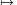{0,1} függvényeket (1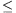 i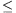 5): legyen f_i(h)=1 pontosan akkor, ha h jelenkezett az i-edik egyetemre. Legyen g=f₁+...+f₅ és 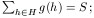a feltételek miatt nyilván 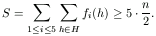Tegyük fel, hogy bármelyik két (különböző) egyetemet kiválasztva, kevesebb mint n/5 diák jelentkezett mindkét intézménybe. Ekkor

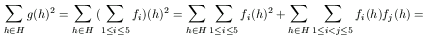
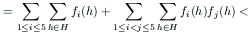
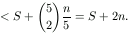
Másrészt, a számtani és a négyzetes közép közti egyenlőtlenség szerint

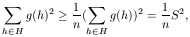
ezért 1/n^.S²<S+2n, azaz 0>S²-nS-2n²=(S-2n)(S+n) . Tehát S<2n, ami ellentmond annak, hogy S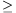 5^.n/2 .

B. 3379. Legyen az ABC háromszögben az AA₁, BB₁, CC₁ szögfelezők metszéspontja O. Igazoljuk, hogy 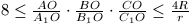, ahol R a köréírt, r a beírt kör sugarát jelöli. (5 pont)

Javasolta: Bencze Mihály, Brassó

Megoldásvázlat.

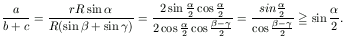
Alkalmazva a szögfelező-tételt

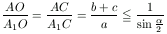
és így

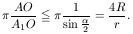
Valamint

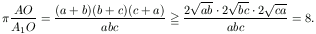
B. 3380. Mutassuk meg, hogy minden paralelepipedonban vagy van olyan csúcs, amelynél a három élszög egyike sem hegyesszög, vagy van olyan csúcs, amelynél a három lapszög egyike sem tompaszög. (4 pont)

Megoldásvázlat. Megyjegyzés: A feladat sajnos hibásan lett kitűzve. Így szólt volna helyesen a feladat: "Mutassuk meg, hogy minden paralelepipedonban vagy van olyan csúcs, amelynél a három élszög egyike sem hegyesszög, vagy van olyan csúcs, amelynél a három élszög egyike sem tompaszög."

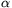
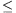
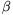
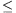
A kitűzött állítás viszont nem igaz, mutatunk egy ellenpéldát. Először is keresünk egy térszöget, melyben mind a három élszög ( 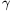) hegyesszög, az egyik lapszög tompaszög, a másik kettő hegyesszög. Ha 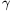=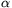+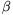, a térszög a síkban marad, az egyik lapszög 180^o, a másik kettő 0^o. Ha 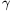-t egy kicsit csökkentjük, a 180^o-os lapszögnél levő él felemelkedik egy kicsit a síkról, ez a lapszög egy kicsit csökken, a másik kettő kicsit növekszik. 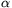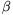Ilyen térszöget kapunk például, ha =30^o, =40^o, =69^o:

Válasszuk ezt a paralelepipedon egyik (az ábrán az A) csúcsához:

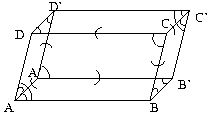
(Az ábrán megjelöltük a hegyes élszögeket és a tompa lapszögeket.)

Az AA' élnél a lapszög tompaszög, a középpontos szimmetria miatt a CC'-nél is tompaszög van. A paralelepipedon AD élére merőleges metszete paralelogramma, az AD-nél levő szöge az AD-nél levő lapszög, tehát hegyesszög, ezért a paralelogrammában a mellette levő két szög tompaszög. Ezek az A'D' és a BC élnél levő lapszögek. Az AB-re merőleges metszetből az AB-nél levő szög gyakorlatilag 0^o-os (azaz nagyon kicsi), így A'B' és DC-nél is tompaszög van. 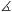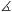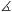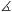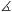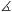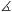A paralelogramma tulajdonságai és a paralelepipedon szimmmetriája miatt A'AB =BB'A' =D'DC =CC'D , DAA' =A'D'D =CBB' =B'C'C , DAB =BCD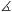 =D'A'B' 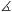=B'C'D' 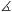, mivel A'AB 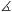, DAA' 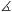, DAB -eket hegyesszögnek választottuk, a felsorolt szögek is azok. Az ábráról jól leolvasható, hogy minden csúcsnál van hegyes élszög és tompa lapszög, erre a testre nem érvényes az állítás, tehát az állítás hamis.

Babos Attila dolgozata alapján

B. 3381. Az osztályfőnök észrevette, hogy az osztályába járó 30 gyerek között van kettő, akinek ugyanazon a napon van a születésnapja. Mutassuk meg, hogy ez nem is olyan meglepő, hiszen annak valószínűsége, hogy 30 ember között van legalább kettő, akinek egy napon van a születésnapja, legalább 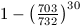. (5 pont)

Megoldásvázlat. Ha 366 napos évvel számolunk, akkor annak a valószínűsége, hogy nincs két olyan ember, aki egy napon született: 366^.365^....^.337/366³⁰. Így annak a valószínűsége, hogy van két ember, akinek egy napon van a születésnapja: 1-366^.365^....^.337/366³⁰. (Ugyanez 365 napos év esetén nagyobb.) Már csak azt kell bizonyítani, hogy 1-366^.365^....^.337/366³⁰>1-(703/732)³⁰, vagyis 703³⁰>732^.730^....^.674. Ez pedig igaz, mert k²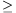 (k+x)(k-x)=k²-x² miatt 703²>732^.674, 703²>730^.676, ... ,703²>704^.702. Mivel ekvivalens átalakításokat végeztünk, ezért az eredeti állítás is igaz.

Csikvári Péter dolgozata alapján

Már regisztráltál?
Új vendég vagy?