Fizikából kitűzött gyakorlatok és feladatok 2000. december

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 220. Készítsünk papírkúpokból vagy félbevágott pingponglabdákból jól csapágyazott szélkereket! Mérjük meg, hogyan függ a kerék fordulatszáma a szél (légáramlás) sebességétől! Következtethetünk-e a mérési adatokból a homorú (konkáv), illetve a domború (konvex) oldalra vonatkozó közegellenállási tényezőkre? (6 pont)

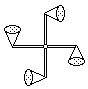
Közli: Gnädig Péter, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3384. Egy téglatest alakú edénybe vizet öntünk. Mekkora az edény magassága, ha mindegyik oldallapra a víz súlyánál nagyobb erő hat? (3 pont)

Lánczos Kornél verseny, Székesfehérvár

P. 3385. Egy 3 m hosszú, méterenként 1 kg tömegű, az asztalon fekvő lánc egyik végére egy 2 dm élű, 2700 kg/m³ sűrűségű alumíniumkockát erősítünk. A kockát megfogjuk, s egyenletesen emeljük 0,5 m/s sebességgel. Mekkora a helyzeti energia változása a) 5 másodpercnyi, b) 10 másodpercnyi emelés után? (3 pont)

Jedlik Ányos verseny (6. és 7. osztály), Nyíregyháza

P. 3386. Hővezető, merev fal oszt két egyenlő részre egy 3 liter térfogatú, hőszigetelt falú tartályt. Mindkét részben 10⁵ Pa nyomású, 300 K hőmérsékletű oxigén van: a bal oldaliban kétatomos (O₂), a jobb oldaliban háromatomos (O₃), vagyis ózon. Az ózon egy idő után kétatomos oxigénné alakul át úgy, hogy két ózonmolekulából három O₂ molekula keletkezik: 2O₃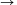3O₂.

a) Mennyi a két részben levő oxigénatomok számának aránya?

b) Mennyi lesz a nyomás és a hőmérséklet az egyes tartályrészekben a termikus egyensúly beállta után, ha minden egyes O₃ molekula átalakulása 2,4^.10^-19 J energiafelszabadulással jár?

(Tekintsük az O₃-at 6, az O₂-t 5 szabadsági fokú ideális gáznak!) (4 pont)

Bethlen Gábor verseny, Hódmezővásárhely

P. 3387. Miért izzadnak sportolás közben a gyerekek általában kevésbé, mint a felnőttek? (4 pont)

Közli: Simon Péter, Pécs

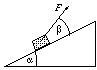
P. 3388. Az 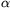hajlásszögű deszkán m tömegű testet csúsztatunk fel egyenletes mozgással. Határozzuk meg a csúsztatáshoz szükséges minimális erő nagyságát és irányát! A súrlódási tényező 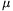. (5 pont)

Közli: Rácz György, Mezőkövesd

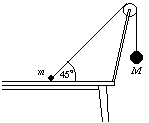
P. 3389. A m és M tömegű, gömb alakú testeket elhanyagolható tömegű csigán átvetett súlytalan fonal köti össze. A két testet az ábrán látható helyzetben tartjuk, és egy adott pillanatban mindkettőt elengedjük. A M tömeg sokkal -- pl. ezerszer -- nagyobb, mint m. Az asztallap és a m tömegű test között a súrlódás elhanyagolható. Elválik-e az elengedést követő pillanatban a m tömegű test az asztallaptól? (5 pont)

Közli: Károlyházy Frigyes, Budapest

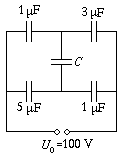
P. 3390. Mekkora legyen az ábrán látható kapcsolásban a C kapacitás, hogy ebben a kondenzátorban a lehető legtöbb energia halmozódjék fel? Mekkora ez a maximális energiamennyiség? (5 pont)

Közli: Légrádi Imre, Sopron

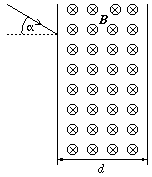
P. 3391. Az ábrán látható d=4 cm szélességű, B=0,02 T indukciójú homogén mágneses mezőbe 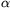=30^o belépési szög alatt, a B vektorra merőlegesen érkezik egy elektronnyaláb.

a) Lassú vagy gyors elektronok tudnak áthaladni a mágneses mezőn?

b) Mekkora feszültséggel gyorsított elektronok ,,verődnek vissza'' a mágneses mezőről? (5 pont)

Közli: Varga István, Békéscsaba

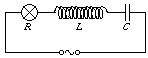
P. 3392. Az ábrán látható soros RLC körben az izzó világít. Azt tapasztaljuk, hogy ha rövidre zárjuk a tekercset, nem változik meg az izzó fénykibocsátása. Hogyan változik az izzó fénykibocsátása, ha a kondenzátort zárjuk rövidre? (4 pont)

Közli: Nagy Márton, Sopron

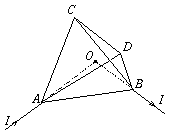
P. 3393. Homogén, egyenletes keresztmetszetű ellenálláshuzalból szabályos tetraédert állítottunk össze. Egy hosszú, egyenes, a tetraéder O középpontjába irányuló vezetéken az A csúcshoz I áramot vezetünk, a B csúcsból pedig hasonló módon elvezetjük. Mekkora és milyen irányú lesz a mágneses indukcióvektor a tetraéder középpontjában? (6 pont)

Közli: Radnai Gyula, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. január 13.