Matematikából kitűzött gyakorlatok és feladatok
2001. január

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

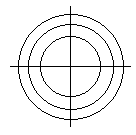
C. 610. Az ábrán látható céltábla három koncentrikus körből és két egymásra merőleges egyenesből áll, amelyek átmennek a körök középpontján. Az így keletkezett 12 rész területe egyenlő. Adjuk meg a három kör sugarának arányát.

C. 611.  Határozzuk meg az a, b, c, d, e számjegyeket úgy, hogy a velük felírt két ötjegyű számra teljesüljön az 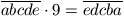egyenlőség.

Reményi Gusztáv, Budapest

C. 612. Az ABC háromszög C csúcsánál derékszög van. Jelölje D a C csúcsból az AB átfogóra bocsátott magasság talppontját. A D-ből a befogókra bocsátott merőlegesek talppontja legyen P és Q. Bizonyítsuk be, hogy a DP és a DQ szakaszok összege legfeljebb akkora, mint a befogók hosszainak harmonikus közepe.

(Az a és b számok harmonikus közepe a reciprokaik átlagának reciproka, azaz 2ab/(a+b).

Varga István, Békéscsaba

C. 613. Messe az ABC háromszög BC oldalával párhuzamos egyenes az AB oldal egyenesét a D, az AC oldal egyenesét az E pontban. Legyen M a BC oldal tetszőleges belső pontja. Mekkora az ADME négyszög területe, ha az ABC háromszög területe T, és az ADE háromszög területe t?

Besenyei Ádám, Tatabánya

C. 614. Az m valós paraméter mely értékeire nincs megoldása az

msin²x+(m-1)sin x+m-2=0

egyenletnek?

Reményi Gusztáv, Budapest

A B pontversenyben kitűzött feladatok

B. 3422. Igazoljuk, hogy 7²⁰⁰¹-3³³³⁵ osztható 100-zal. (3 pont)

B. 3423. Alkothatnak-e egy háromszög beírt körének az oldalakon levő érintési pontjai tompaszögű háromszöget? (3 pont)

B. 3424. Egy szabályos háromszögbe négyzetet írunk, amelynek minden csúcsa a háromszög kerületén van. A négyzet egyik oldala egy kisebb szabályos háromszöget metsz le; ebbe hasonló módon ismét négyzetet írunk, és így tovább. A háromszög hányadrészét fedi le a négyszögek végtelen sorozata? (3 pont)

B. 3425. A 3+4+5+6=3^.6; 15+16+17+...+34+35=15^.35 egyenlőségek azt sugallják, hogy a természetes számokból ki lehet választani néhány egymás követőt úgy, hogy összegük egyenlő a legkisebb és a legnagyobb kiválasztott szám szorzatával. Mutassuk meg, hogy végtelen sok ilyen tulajdonságú sorozat van! (5 pont)

Kiss Sándor, Nyíregyháza

B. 3426. Mit kapunk maradékul, ha az x²⁰⁰¹ polinomot elosztjuk (x+1)²-nel? (4 pont)

B. 3427. Tükrözzük a hegyesszögű ABC háromszög oldalegyeneseit a rájuk nem merőleges magasságvonalakra. Az így kapott hat tükörkép közül három az ABC háromszög belsejében fekvő A₁B₁C₁ háromszöget, míg a másik három az A₂B₂C₂ háromszöget határolja. Ez utóbbi háromszögnek van egy 20^o-os és egy 70^o-os szöge. Számítsuk ki az A₁B₁C₁ háromszögek szögeit. (4 pont)

Bakonyi Gábor, Budapest

B. 3428. Bizonyítsuk be, hogy tetszőleges háromszögben érvényes az alábbi összefüggés:

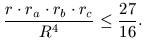
(R a háromszög köré írt, r a háromszögbe írt, r_a, r_b, r_c pedig a hozzáírt körök sugarát jelentik.) (4 pont)

Tőricht Pál és Árokszállási Tibor, Paks

B. 3429. Legyen 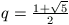, és legyen f:N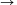N egy olyan függvény, amelyre tetszőleges pozitív egész n esetén

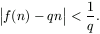
Igazoljuk, hogy f(f(n))=f(n)+n.

(4 pont)

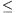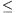B. 3430. Adottak a síkon a P₁, P₂, ..., P_n pontok. Kiválasztunk egy olyan 1in indexet, amelyre a P_i, P_i+1, P_i+2 pontok nincsenek egy egyenesen, és a P_iP_i+1P_i+2 háromszög negatív körüljárású. (Az indexelés ciklikus). A P_i+1 pontot kicseréljük arra a pontra, amit úgy kapunk, hogy P_i+1-et tükrözzük a P_iP_i+2 szakasz felezőpontjára. Ezt mindaddig ismételjük, amíg csak létezik megfelelő i index. Bizonyítsuk be, hogy tetszőleges pontokból kiindulva az eljárás véges sok lépés után véget ér. (5 pont)

B. 3431. OKOSBANK páncélszekrényén több különböző zár van. A bankban n pénztáros dolgozik, mindegyiknek kulcsa van a zárak némelyikéhez. (Egy pénztárosnak több kulcsa is lehet, és egy zárhoz többüknek is lehet kulcsa.) Tudjuk, hogy bármelyik k pénztáros együtt mindig ki tudja nyitni a páncélszekrényt, de k-1 pénztáros soha. Legalább hány zár van a páncélszekrényen? (5 pont)

Vígh Viktor, Szeged

A pontversenyben kitűzött nehezebb feladatok

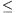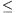A. 254.  Adottak a síkon a P₁, P₂, ..., P_n pontok. Ezekkel a pontokkal a következő műveletet végezhetjük: Kiválasztunk egy olyan 1in indexet, amelyre a P_i, P_i+1, P_i+2 pontok nincsenek egy egyenesen, és a P_iP_i+1P_i+2 háromszög negatív körüljárású. A P_i+1 pontot kicseréljük arra a pontra, amit úgy kapunk, hogy P_i+1-et tükrözzük a P_iP_i+2 szakaszra. Ezt a műveletet mindaddig ismételjük, amíg csak létezik megfelelő i index. Bizonyítsuk be, hogy tetszőleges pontokból kiindulva, az eljárás véges sok lépés után véget ér.

A. 255.  Legyen 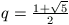, és definiáljuk a pozitív egészeken értelmezett f függvényt a következőképpen.

1. Legyen f(1)=2;

2. Ha f(1), ..., f(n-1)-et már definiáltuk, és az n nem szerepel ezek között, akkor legyen f(n)=f(n-1)+1;

3. Ha f(1), ..., f(n-1)-et már definiáltuk, és az n szerepel ezek között, akkor legyen k a legkisebb pozitív egész, amelyre f(k)=n, és legyen f(n)=n+k.

Igazoljuk, hogy tetszőleges n pozitív egészre

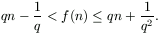
A. 256. Van n golyó, mindegyiknek szeretnénk megtudni a súlyát. Ehhez rendelkezésünkre áll egy olyan egykarú mérleg, amellyel egyszerre egy vagy két golyó súlyának összegét lehet meghatározni. Arra is fel kell készülnünk, hogy esetleg az egyik mérés pontatlan lesz. Jelöljük f(n)-nel azt a minimális mérésszámot, amellyel az összes golyó súlya minden esetben biztosan meghatározható. Igazoljuk, hogy

f(n)<n+log₃n+3.

Surányi László és Virág Bálint ötletéből

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. február 15.