Matematikából kitűzött gyakorlatok és feladatok
2001. február
Kérjük, olvassa el a versenykiírást.
 |
A C pontversenyben kitűzött (könnyebb) gyakorlatok |
C. 615. Egy háromtételes zenemű lejátszása 60 percig tart. Egyik tétel sem hosszabb, mint a másik két tétel együttvéve. Bármelyik két tétel hossza között legalább 3 perc különbség van. Milyen határok között változhat a legrövidebb tétel időtartama?
C. 616. Lehetséges-e, hogy egy nyolctagú társaságban az ismetetségek száma rendre
a) 1, 3, 3, 4, 5, 6, 6, 6;
b) 1, 3, 3, 4, 5, 6, 6, 7?
C. 617. Az ABC egyenlő szárú háromszögben az AB alap felezőpontja D, a D-ből CB-re állított merőleges talppontja P, a DP szakasz felezőpontja F. Fejezzük ki az AFPC négyszög területét a CF és az AP segítségével.
C. 618. Egy ABCD téglalap hosszabbik oldala AB, P az AB szakasz, Q a CD szakasz belső pontja. Igazoljuk, hogy P-nek és Q-nak pontosan egy olyan helyzete van, amelyben APCQ rombusz. Mutassuk meg, hogy a téglalap oldalainak arányát változtatva a rombusz és a téglalap területének aránya 1/2 és 1 között bármilyen értéket felvehet.
C. 619. 1-től 100 000-ig hány olyan n egész szám van, amelyre n3+23n többszöröse a 24-nek?
 |
A B pontversenyben kitűzött feladatok |
B. 3432. Az alábbi táblázat a Pascal-háromszög mintájára készült. Az első sor két eleme 1 és 2, ezután pedig minden újabb szám a felette álló kettő összege.
| 1 | 2 | |||||||
| 1 | 3 | 2 | ||||||
| 1 | 4 | 5 | 2 | |||||
| 1 | 5 | 9 | 7 | 2 | ||||
a) Mennyi a 100-adik sorban álló számok összege?
b) Mit kapunk, ha a 100-adik sorban váltakozó előjellel adjuk össze a számokat?
c) Mennyi a 100-adik sor 47-edik eleme? (4 pont)
B. 3433. Egy geometria konferencia résztvevői a szünetben olyan szendvicseket kaptak, amelyek mindegyikén egy téglatest alakú kenyéren egy vastag szelet henger alakú sajt és egy gömb alakú húspogácsa volt. Mindig ketté lehet-e vágni egy ilyen szendvicset egyetlen egyenes vágással úgy, hogy a két rész kenyérből, húsból és sajtból is ugyanannyit tartalmazzon? (4 pont)
B. 3434. Egy trapéz alapjai a és b. A trapéz elmetszhető az alapokkal párhuzamos egyenessel úgy, hogy a két rész-trapézba kör írható. Mekkora az eredeti trapéz kerülete? (3 pont)
Javasolta: Reményi Gusztáv, Budapest
B. 3435. Keressük meg az alábbi egyenletrendszer nemnegatív megoldásait:
x1+x2+x3+...+x100=5050
x22-x12=3, ..., xk2-xk-12=2k-1, ..., x1002-x992=199.
(4 pont)
B. 3436. Az egységnyi területű ABC háromszög AB, BC, CA oldalain adottak a C1, A1, B1 pontok úgy, hogy
AC1/C1B=1/2,
BA1/A1C=1/3,
CB1/B1A=1/4.
Mekkora területű háromszöget határolnak az AA1, BB1, CC1 egyenesek? (3 pont)
B. 3437. Egy egyenesen ebben a sorrendben adottak az A, B, C, D pontok úgy, hogy BC=2AB, CD=AC. Bizonyítsuk be, hogy bárhogyan is rajzolunk egy-egy kört az A és C, illetve a B és D pontokon keresztül, akkor ezek közös húrja felezi az AC szakaszt. (4 pont)
B. 3438. Az f(x,y,;z) függvényre teljesül, hogy bármely t valós számra
f(x+t,y+t,z+t)=t+f(x,y,z);
f(tx,ty,tz)=tf(x,y,z);
f(x,y,z)=f(y,x,z)=f(x,z,y).
Mennyi f(2000, 2001, 2002)? (5 pont)
B. 3439. Jelöljön p egy pozitív számot, és tekintsük az 1, p, 1/p, p2, 1/p2, ..., pn, 1/pn ... végtelen sorozatot. Mely p számokra igaz, hogy minden pozitív szám tetszőleges pontossággal megközelíthető a fenti sorozat véges sok alkalmas elemének összegével? (5 pont)
B. 3440. Az A, B, C
pontok tükörképe egy e egyenesre A1, B1,
C1, egy P pontra pedig
A2, B2, C2. Mi a
P tükörképe az e egyenesre, ha 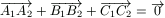 ?
?
3 pont
B. 3441. Pinokkiónak 9-féle akadályon kell sikerrel túljutnia, hogy hús-vér gyerek lehessen. Nehéz dolga van; ha egy akadályon elbukik, akkor vissza kell térnie az előzőhöz, és ott újra kell próbálkoznia. Ha a legelső akadályon bukik el, akkor fabábu marad örökre. Pinokkió nem tanul a kudarcokból, ezért az egyes akadályokon a siker valószínűsége mindig 1/10, 2/10, 3/10, ..., 9/10, akárhányadszor is próbálkozik. Milyen sorrendben rendezze el a Kékhajú Tündér a Pinokkióra váró akadályokat ahhoz, hogy Pinokkió a legnagyobb eséllyel változzék át igazi gyerekké, és mekkora ebben az esetben a siker valószínűsége? (5 pont)
 |
A pontversenyben kitűzött nehezebb feladatok |
A. 257. Van n golyó, mindegyiknek szeretnénk megtudni a súlyát. Ehhez rendelkezésünkre áll egy olyan egykarú mérleg, amellyel egyszerre egy vagy két golyó súlyának összegét lehet meghatározni. Arra is fel kell készülnünk, hogy esetleg az egyik mérés pontatlan lesz. Jelöljük f(n)-nel azt a minimális mérésszámot, amellyel az összes golyó súlya minden esetben biztosan meghatározható. Igazoljuk, hogy
f(n)>n+log 3n-3.
Surányi László és Virág Bálint ötletéből
A. 258. Adott az e egyenesen hat
különböző pont: A, B, C, D, E és
F. Tudjuk, hogy 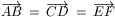 . Szerkesszünk
egyetlen egyenes vonalzóval olyan egyenest, amely párhuzamos e-vel.
. Szerkesszünk
egyetlen egyenes vonalzóval olyan egyenest, amely párhuzamos e-vel.
A. 259. Az x1, x2, ...,
xn, valamint y1<y2<...<yn pozitív valós számokra és az u>1 valós
számra teljesül, hogy tetszőleges 1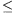 k
k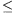 n esetén
n esetén
x1u+x2u+...+xku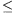 y1u+y2u+...+yku.
y1u+y2u+...+yku.
Bizonyítsuk be, hogy
x1+x2+...+xn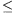 y1+y2+...yn.
y1+y2+...yn.
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

