Matematikából kitűzött gyakorlatok és feladatok
2001. március

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 620. Egy trapézt szimmetrikus trapéznak nevezünk, ha alapjainak felező merőlegese egybeesik. Igaz-e, hogy ha egy trapéz szimmetrikus, akkor szimmetrikus trapéz?

C. 621. Egy sütödében, ahol mazsolás kalácsot is készítenek, a pék azt szeretné, ha a kalácsok bármely 4 dkg-os szeletében legalább 0,99 valószínűséggel lenne mazsola. 1 kg kalács elkészítéséhez hány szem mazsolát keverjen a tésztához?

C. 622. Adjuk meg az összes olyan 7-tel osztható 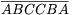$\overline{ABCCBA}$ alakú hatjegyű számot, amelyre $\displaystyle \overline{ABC}$ is 7-tel osztható. (A, B, C különböző számjegyeket jelölnek.)

C. 623. Oldjuk meg a következő egyenletrendszert:

$\displaystyle \eqalign{a^2b^2-a^2-ab+1&=0\cr a^2c-ab-a-c&=0\cr abc&=-1.\cr}$

Javasolta: Kiss Sándor, Szatmárnémeti

C. 624. Belefér-e százezer darab 4 cm átmérőjű szabványos pingponglabda egy 200x164x146 cm méretű ládába?

A B pontversenyben kitűzött feladatok

B. 3442. Van-e olyan 2001 jegyű természetes szám, amely -- a tízes számrendszerben felírva -- megegyezik a 2001-edik hatványának utolsó 2001 számjegyével? (4 pont)

Javasolta: Kiss Tamás, Budapest

B. 3443. Az ABCD téglalap CB oldalának B-n túli meghosszabbítására, valamint a CD oldalának D-n túli meghosszabbítására egyenlő hosszúságú szakaszokat mértünk fel. Így kaptuk az F, illetve az E pontokat. Igazoljuk, hogy az EB és az FD egyenesek metszéspontját A-val összekötő egyenes felezi az A csúcsnál lévő szöget. (3 pont)

B. 3444. A pozitív egész számokból álló végtelen a₁, a₂, a₃, ... a_n, ... sorozatban jelölje f_n az n természetes szám előfordulásainak a számát, ha ez az érték véges.

Az a₁, a₂, ... a_n, ... sorozat ,,gyakoriságsorozata'' ezután az f₁, f₂, ... f_n, ... sorozat, ha minden f_i véges. Hasonlóan értelmezzük a fenti f₁, f₂, ... f_n, ... sorozat gyakoriságsorozataként az a₁, a₂, ... a_n, ... sorozat másodrendű gyakoriságsorozatát, ha minden gyakoriság véges, és ennek gyakoriságsorozataként a harmadrendű gyakoriságsorozatot és így tovább.

Van-e olyan a₁, a₂, ... a_n, ... sorozat, amelynek minden k-ra létezik a k-adrendű gyakoriságsorozata? (4 pont)

B. 3445. Van-e olyan háromszög, amelyet valamelyik oldalával párhuzamosan ketté lehet vágni úgy, hogy a két rész kerülete is és területe is egyenlő? (4 pont)

Javasolta: Reményi Gusztáv, Budapest

B. 3446. Határozzuk meg a q(x) polinomot úgy, hogy a p(x)=x²+x+1 polinommal p²(x)-2p(x)q(x)+q²(x)-4p(x)+3q(x)+3 equiv 0 azonosság teljesüljön. (4 pont)

B. 3447. Az ABC háromszög oldalait pozitív körüljárás szerint kétszeresére nyújtjuk, majd ugyanezt megismételjük a kapott A₁B₁C₁ háromszögre, ezúttal negatív körüljárás szerint. Bizonyítsuk be, hogy az így kapott A₂B₂C₂ háromszög hasonló az ABC háromszöghöz. Milyen hasonló állítás igaz négyszögekre? (4 pont)

B. 3448. Mutassuk meg, hogy adott ellipszisbe írt olyan háromszögek területe, amelyek súlypontja egybeesik az ellipszis középpontjával, állandó. (4 pont)

Javasolta: Kiss Sándor, Szatmárnémeti

B. 3449. Legyen a>1 adott egész szám. Bizonyítsuk be, hogy ha az x²-ay²=-1 egyenletnek van egész megoldása, akkor végtelen sok egész megoldása van. (5 pont)

Javasolta: Fried Ervin, Budapest

B. 3450. Tekintsük azokat a síkokat, amelyek a T tetraéder lapsíkjaival párhuzamosak, és a T-ből általuk levágott kis tetraéderek térfogata T térfogatának 1/3 része. A T térfogatának hányadrésze marad meg, ha csúcsait levágjuk ezekkel a síkokkal? (5 pont)

B. 3451. Oldjuk meg a következő egyenletet: $\arcsin x+\arcsin\sqrt{15}x=\pi/2$ . (4 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 260. Adott az e egyenesen négy különböző pont: A, B, C és D, és tudjuk, hogy 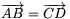$\overrightarrow{AB}=\overrightarrow{CD}$ . Létezik-e olyan, egyetlen egyenes vonalzót használó szerkesztési eljárás, amely egy e-vel párhuzamos egyenest szerkeszt meg?

A. 261. Aladár és Benedek egységnyi oldalú szabályos háromszögekből összerakott egy n oldalú szabályos háromszöget. Az így kapott táblán a következő játékot játsszák: Felváltva kiszíneznek egy-egy csúcspontot a piros, kék és zöld színek valamelyikével mindaddig, amíg az összes csúcs, beleértve a nagy háromszög oldalain és belsejében levő pontokat is, ki lesz színezve. Minden olyan egységnyi oldalú háromszögért, amelynek csúcsai piros-kék-zöld színűek pozitív körüljárás szerint, az első lépést megtevő Aladár kap egy pontot. Azokért a háromszögekért, amelyeknek csúcsai piros-kék-zöld színűek negatív körüljárás szerint, Benedek kap egy-egy pontot. Az nyer, aki több pontot szerez.

Kinek van nyerő stratégiája?

A. 262. 0<a<b<c egész számok. Bizonyítsuk be, hogy léteznek olyan x, y, z egész számok, amelyek nem mind 0-k, ax+by+cz=0 és |x|, |y|, |z| mindegyike kisebb, mint $\displaystyle {2\over{\sqrt3}}\sqrt c$.

2000. évi Schweitzer-feladat alapján

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?