Matematikából kitűzött gyakorlatok és feladatok
2001. április
Kérjük, olvassa el a versenykiírást.
 |
A C pontversenyben kitűzött (könnyebb) gyakorlatok |
C. 625. A McDonald's éttermekben 6-os, 9-es vagy 20-as csomagolásban rendelhetünk Chicken McNuggets-et. (Így például kérhetünk 21 darabot, mert 21=6+6+9, de semmilyen módon nem kaphatunk 19 darabot.) Melyik az a legnagyobb darabszám, amit nem tudunk rendelni?
C. 626. Az 5 egység sugarú körlapot vágjuk szét két húrral három egyenlő területű részre. Milyen hosszúak ezek a húrok?
Javasolta: Reményi Gusztáv, Budapest
C. 627. Oldjuk meg a következő egyenletrendszert:
a+b=c+d,
a3+b3=c3+d3.
Javasolta: Ábrány Miklós, Beregszász
C. 628. Egy tetraéder alakú kartondobozt felvágunk az egyik csúcsából induló három éle mentén, majd az ,,elváló'' lapokat leterítjük a fenti csúccsal szemközti lap síkjába. Így egy 30 cm oldalú négyzetet kapunk. Mekkora a tetraéder térfogata?
C. 629. Igazoljuk, hogy ha tizenhárom egész szám összege osztható 6-tal, akkor a tizenhárom szám tizenharmadik hatványának összege is osztható 6-tal.
Javasolta: Székelyhidi Tamás, Ercsi
 |
A B pontversenyben kitűzött feladatok |
B. 3452. Két játékos egy 5x5-ös táblázat mezőibe felváltva jeleket ír; a kezdő játékos mindig egy X jelet, a második pedig mindig két O jelet. Az nyer, akinek először van öt jele egy sorban vagy egy oszlopban. Milyen stratégiát kövessen a második játékos, ha nyerni akar? (4 pont)
Javasolta: Gyanta Nándor, Budapest
B. 3453. Legyen az ABC háromszög súlypontja S, az AS szakasz felezőpontja H, az AB oldal felezőpontja Q. Messe a H-n keresztül BC-vel húzott párhuzamos az AB oldalt P-ben, a CQ egyenest R-ben. Mekkora a PQR és az APH háromszögek területének aránya? (3 pont)
Javasolta: Káspári Tamás, Paks
B. 3454. Van 27 darab 1 cm élű kockánk.
a) Ki lehet-e festeni ezek lapjait lilára, fehérre és sárgára úgy, hogy a készletből lila, fehér, valamint sárga felszínű 3x3x3-as kockát is össze lehessen állítani? {\item}
b) Legalább hány lapot kell lilára festenünk ahhoz, hogy biztosan összerakható legyen az egységkockákból egy lila felszínű 3 cm élű kocka? (4 pont)
B. 3455. Adjunk meg végtelen sok (m, n) számpárt úgy, hogy az m, n különböző egész számoknak ugyanazok legyenek a prímosztói, és az m+1, n+1 számoknak is ugyanazok legyenek a prímosztói. (5 pont)
Javasolta: Gyanta Nándor, Budapest
B. 3456. Egy tetraéder éleire pozitív egész számokat írunk. Egy lépésben a következő módon változtathatjuk meg az élekre írt számokat. Kiválasztunk egy csúcsot, és a belőle induló három élre írt számok helyébe a következőket írjuk: egy-egy élre a kiválasztott csúcsból induló másik két élre írt számok különbségét úgy, hogy az a és b számok különbségének felírásakor szabadon választhatunk a-b és b-a közül, a harmadik élre pedig a kiválasztott csúcsból induló másik két élre írt számok összegét. Előfordulhat-e, hogy néhány lépés után minden élen 0 áll? (3 pont)
Javasolta: Mezei József, Vác
B. 3457. Határozzuk meg azon p, q pozitív prímeket, amelyekre az x4+p2x+q=0 egyenletnek van többszörös gyöke. (4 pont)
Javasolta: Besenyei Ádám, Budapest
B. 3458. Adott a síkon n piros pont. Mutassuk meg, hogy elhelyezhető 2n kék pont úgy, hogy a piros pontok által meghatározott minden háromszög belsejében van legalább egy kék. (5 pont)
B. 3459. Egy ABCD paralelogramma A, B, C, D csúcsai köré a, b, c, d sugarú egymáson kívül elhelyezkedő köröket rajzolunk úgy, hogy a+c=b+d. Mutassuk meg, hogy a szemközti csúcsok köré rajzolt körök két-két közös külső érintője érintőnégyszöget határoz meg. (4 pont)
B. 3460. Egy háromszögben a beírt körnek a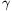 
szöggel szemközti oldalon lévő
érintési pontja az oldalt x és y hosszú szakaszokra
osztja. Bizonyítsuk be, hogy a háromszög területe \(\displaystyle xy\ctg{{\gamma}\over2}\). (4 pont)
Javasolta: Besenyei Ádám, Budapest
B. 3461. Legyenek a>0 és c\(\displaystyle ne\)0 adott egész számok. Bizonyítsuk be, hogy ha az x2-ay2=c egyenletnek van legalább 4c2+1 különböző egész megoldása, akkor végtelen sok egész megoldása van. (5 pont)
Javasolta: Fried Ervin, Budapest
 |
A pontversenyben kitűzött nehezebb feladatok |
A. 263. Adott egy körön n piros és n kék ív úgy, hogy bármely piros ív metsz bármely kék ívet. Bizonyítsuk be, hogy van olyan pont a körön, amelyet legalább n színes ív fed le.
Schweitzer Miklós Matematikai Emlékverseny, 2000
A. 264. A (0, 1) intervallum racionális elemeinek a p valós együtthatós polinom szerinti képe egy másik intervallum racionális elemeinek halmaza. Bizonyítsuk be, hogy p legfeljebb elsőfokú.
Fried Ervin, Budapest
A. 265. Definiáljuk az a1, a2, ... sorozatot a következő rekurzióval.
\(\displaystyle a_1=a_2=a_3=1;\qquad a_{n+1}={a_n^2+a_{n-1}^2\over a_{n-2}}\qquad(n=3,\;4,\;\dots)\)
Igazoljuk, hogy a sorozat egész számokból áll.
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)