A 2001. októberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3482. Négy jóbarát észrevette, hogy ha elosztják a könyveik számát a számjegyek összegével, akkor eredményül mind a négyen ugyanazt az egész számot, 13-at kapják. Bizonyítsuk be, hogy legalább kettejüknek ugyanannyi könyve van. (4 pont)

Javasolta: Gerőcs László, Budapest

Megoldás. Tekintsük bármelyik jóbarát könyveinek a számát. Azt állítjuk, hogy ezen szám jegyeinek száma pontosan 3. Először is, ha legfeljebb 2 lenne, akkor a szám alkalmas a,b számjegyek segítségével 10a+b alakban állítható elő, ahol a+b éppen a számjegyek összege. De ekkor 0<10a+b<13(a+b). Ha pedig a szám n$\displaystyle ge$4 jegyű lenne, akkor számjegyeit a₁,a₂,...,a_n-nel jelölve

10^n-1$\displaystyle le$10^n-1a₁+10^n-2a₂+...+a_n=13(a₁+a₂+...+a_n)$\displaystyle le$13^.9^.n<200n ,

10^n-3<2n adódna. Azonban n$\displaystyle ge$4 esetén 10^n-3>2n, ami n=4 esetén nyilván fennáll, egyébként pedig például indukcióval könnyen igazolható.

A könyvek száma tehát 100a+10b+c, ahol az a,b,c számjegyekre a$\displaystyle ge$1 és 100a+10b+c=13(a+b+c), vagyis 29a=b+4c$\displaystyle le$35. Ezért a=1 és 20$\displaystyle le$4c$\displaystyle le$29, ahonnan c lehetséges értékei 5,6 és 7. Bármelyik jóbarátnak tehát 195, 156 vagy 117 könyve van, így kell legyen közöttük kettő, akinek ugyanannyi könyve van.

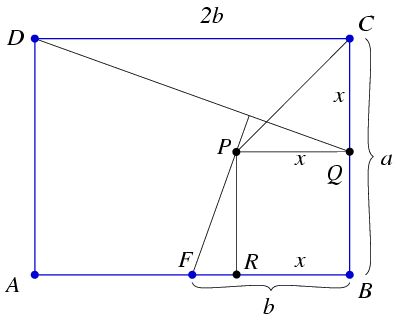
B. 3483. Az ABCD téglalap AB oldalának felezőpontja F. A C-ből induló szögfelező egy P pontjának vetülete a BC egyenesre Q. Bizonyítsuk be, hogy ha a PF egyenes merőleges a DQ egyenesre, akkor AP=BC. (3 pont)

Megoldás. Jelölje a P pont vetületét az AB egyenesre R. Jelölje továbbá a CB, BF és CQ szakaszok hosszát a,b, illetve x. Ha a PF egyenes merőleges a DQ egyenesre, akkor a DCQ háromszög hasonló a PRF háromszöghöz. Ezért CQ/CD=RF/RP, vagyis x/(2b)=(b-x)/(a-x), ahonnan ax-x²=2b²-2bx, majd rövid átalakítás után (2b-x)²+(a-x)²-a²=0 adódik. Következésképpen AP²=AR²+RP²=(2b-x)²+(a-x)²=a²=BC², vagyis valóban AP=BC. A fenti gondolatmenet alapján azt sem nehéz megmutatni, hogy a P$\displaystyle ne$F feltétel mellett az állítás megfordítható.

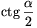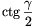B. 3484. Egy háromszög $alpha$ , $beta$ , $gamma$ szögeire $\ctg{\alpha\over2}$ , $\displaystyle \ctg{\beta\over2}$, $\ctg{\gamma\over2}$ egymást követő egész számok. Mekkora a háromszög legnagyobb szöge? (3 pont)

Megoldás. Legyen $\displaystyle \ctg{{\beta}\over2}=A$. Ha \(\displaystyle 0x>0, ezért A pozitív egész szám.

$\displaystyle A=\ctg{{\beta}\over2}=\ctg({\pi\over2}-{{\alpha}\over2}-{{\gamma}\over2})=\tan({{\alpha}\over2}+{{\gamma}\over2})={\tan{{\alpha}\over2}+\tan{{\gamma}\over2}\over1-\tan{{\alpha}\over2}\tan{{\gamma}\over2}}=$

$\displaystyle ={1/(A-1)+1/(A+1)\over1-1/(A^2-1)}={2A\over A^2-2}\ ,$

ahonnan A²-2=2, A=2 adódik. Ezért $\displaystyle \ctg{{\alpha}\over2}=1$, vagyis $\displaystyle \alpha={\pi\over2}$ a háromszög legnagyobb szöge. (Megjegyezzük, hogy ilyen háromszög valóban létezik.)

B. 3485. Az A halmaz elemei pozitív egész számok, és tetszőleges x, y$\displaystyle in$A, x>y esetén 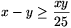$x-y\geq{xy\over25}$ . Legfeljebb hány eleme lehet az A halmaznak? (4 pont)

Vojtech Jarnik matematikaverseny, Ostrava, 2001

1. megoldás. A feltétel rövid átalakításával azt látjuk, hogy ha x,y$\displaystyle in$A és x>y, akkor 25>25x/(x+25)$\displaystyle ge$y. Az A halmaznak tehát legfeljebb egy kivétellel az összes eleme kisebb 25-nél, következésképpen csak véges sok eleme lehet, jelölje ezeket x₁>x₂>...>x_n. Már láttuk, hogy ha n>1, akkor x₂$\displaystyle le$24.

Ha 0<a<b, akkor 25a/(a+25)<25b/(b+25), amint arról a törteket közös nevezőre hozva egyszerűen meggyőződhetünk. A 25x/(x+25) függvény tehát a pozitív számok halmazán szigorúan monoton növekedő.

Ennek alapján így okoskodhatunk. Ha n$\displaystyle ge$3, akkor 13>25^.24/49$\displaystyle ge$25x₂/(25+x₂)>x₃. Továbbá, ha n$\displaystyle ge$4, akkor 9>25^.12/37$\displaystyle ge$25x₃/(25+x₃)>x₄, ha n$\displaystyle ge$5, akkor 7>25^.8/33$\displaystyle ge$25x₄/(25+x₄)>x₅, és ha még n$\displaystyle ge$6 is fennáll, akkor 5>25^.6/31$\displaystyle ge$25x₅/(25+x₅)>x₆. Következésképpen minden i$\displaystyle ge$0 esetén x_6+i$\displaystyle le$4-i, tehát n$\displaystyle le$9, az A halmaznak legfeljebb 9 eleme lehet.

Végül mutatunk egy 9 elemű A halmazt amely kielégíti a feltételeket. Itt lényegében a fenti gondolatmenet megfordításáról van szó. Legyen A={x₁,x₂,...,x₉}, ahol x₉=1,x₈=2,x₇=3,x₆=4,x₅=6,x₄=8,x₃=12,x₂=24 és x₁=600. Legyen 1$\displaystyle le$i<j<k$\displaystyle le$9. Ha $\displaystyle x_i-x_j\ge{x_ix_j\over25}$ fennáll, akkor $\displaystyle x_i-x_$x_i-x_j\ge{x_ix_j\over25}>{x_ix_k\over25}">, ezért csak azt kell ellenőriznünk, hogy minden 1$\displaystyle le$i$\displaystyle le$8 esetén $\displaystyle x_i-x_{i+1}\ge{x_ix_{i+1}\over25}$ teljesül. Ez pedig valóban így is van.

2. megoldás. A feltételt átrendezve, tetszőleges x,y$\displaystyle in$A esetén $\displaystyle \left|{1\over x}-{1\over y}\right|\ge{1\over25}$. A halmaz elemeinek reciprokai tehát páronként legalább 1/25 távolságra vannak egymástól. Ebből következeik, hogy a $\displaystyle (0,{1\over5})$ intervallumban legfeljebb 5 elem reciproka lehet, vagyis legfeljebb 5 elem lehet 4-nél nagyobb. Az elemek száma tehát nem lehet nagyobb, mint 9.

Kilenc elem lehetséges. Ha a halmaz elemei 1, 2, 3, 4, 5, 7, 10, 17, 54, akkor bármely két reciprok különbsége nagyobb, mint 1/25. (A megoldásból az is látszik, ezt elég a szomszédos elemekre ellenőrizni.)

B. 3486. Adott a síkon 2001 pont és egy egységnyi sugarú körvonal. Bizonyítsuk be, hogy található a körvonalon olyan pont, amelytől az adott pontokig mért távolságok összege legalább 2001. (4 pont)

Nemzetközi Magyar Matematika Verseny, 2001

Megoldás.

Legyen A és B a kör egy átmérőjének két végpontja, az adott pontok pedig legyenek P₁,P₂,...,P₂₀₀₁. A háromszög- egyenlőtlenség szerint ekkor minden i-re igaz, hogy

AP_i+BP_i$\displaystyle ge$AB=2,

azaz

$\displaystyle \sum_{i=1}^{2001}AP_i+\sum_{i=1}^{2001}BP_i\geq2\cdot2001=4002.$

Ebből azonnal adódik, hogy A és B közül legalább az egyik eleget tesz a feladat feltételeinek.

B. 3487. Határozzuk meg mindazokat a pozitív valós számok halmazán értelmezett f függvényeket, amelyek az értelmezési tartományukban mindenütt eleget tesznek az 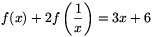$f(x)+2f\left({1\over x}\right)=3x+6$ összefüggésnek. (3 pont)

Megoldás. Legyen x tetszőleges pozitív valós szám, ekkor 1/x is az. Ezért a feladatban szereplő f függvényekre f(x)+2f(1/x)=3x+6 és f(1/x)+2f(x)=3/x+6 is teljesül. Ezeket összeadva és a kapott egyenlőség minkét oldalát 3-mal osztva f(x)+f(1/x)=x+1/x+4 adódik. Ha ezt a második egyenlőségből kivonjuk, kapjuk, hogy f(x)=2/x-x+2. Egyetlen ilyen f függvény létezhet tehát, mégpedig az az f függvény, amelyik minden pozitív valós x helyen az f(x)=2/x-x+2 értéket veszi fel. Ez pedig valóban meg is felel a kívánalomnak.

B. 3488. Egy téglalap alakú ABCD biliárdasztal oldalai AB=150 cm, BC=205 cm. Az asztalon négy lyuk van, ezek a csúcsokban találhatók. Az A csúcsból (a lyuk felől) ellökünk egy golyót az asztal oldalával 45^o-os szöget bezáró irányban. Valahányszor az asztal széléhez ér, a golyó rugalmasan visszapattan. Mi történik a golyóval? (4 pont)

Megoldás. Ideális helyzetet feltételezve, a golyó mozgása során nem veszít sebességéből. Az asztal AB és CD oldalait osszuk fel 150 egyenlő részre, a BC és DA oldalakat pedig 205 egyenlő részre. (Oszthatnánk a megfelelő oldalakat 30, illetve 41 egyenlő részre is, de ez a megoldás szempontjából nem jelent lényeges egyszerűsítést). A golyó útja az asztalon egy töröttvonal, amely egymás után az s₁,s₂,... szakaszokból áll. Mivel a golyó mindig az asztal oldalaival 45^o-os szöget bezáró irányban halad, az asztal szélét mindig valamelyik osztópontnál (a sarkokat is ideeértve) éri el, hiszen ha az s_i szakasz kezdőpontja egy osztópont, akkor könnyű látni, hogy a végpontja is az lesz.

Először is megmutatjuk, hogy nem érhet kétszer ugyanahhoz az osztóponthoz ugyanabból az irányból. Valóban, ha s_i=s_j (i<j), és ezeket a golyó ugyanabban az irányban futja be, akkor ugyanez igaz az s_i-1 és s_j-1 szakaszokra is. Így indukcióval adódik, hogy az s_j-i+1 szakasz kezdőpontja megegyezik az s₁ kezdőpontjával, vagyis a golyó már az s_j-i szakaszt megtéve beleesett volna az A csúcsnál lévő lyukba.

A golyó tehát útja során minden osztópontot legfeljebb kétszer érinthet, ami azt jelenti, hogy útja csak véges sok szakaszból áll, előbb-utóbb tehát el kell tűnnie valamelyik lyukban. A kérdés most már csak az, hogy melyikben.

Tegyük fel először azt, hogy az A csúcsnál lévő lyukban tűnik el az s_n szakasz megtétele után. Ekkor az útját `megfordítva' láthatjuk, hogy s_n=s₁ és ezt a két szakaszt a golyó ellentétes irányban futja be. Hasonló igaz tehát az s_n-1 és s₂ szakaszokra is, és így tovább. Ez azt jelenti, hogy n páros kell legyen és a két középső szakasz meg kell egyezzen, ez azonban lehetetlen.

Megmutatjuk, hogy a golyó a D csúcsnál sem tűnhet el. Ekkor ugyanis a golyó útja szimmetrikus lenne az asztal AB oldallal párhuzamos szimmetriatengelyére, ami csak úgy lehetne, ha a szakaszok száma páros lenne és a két középső szakasz közös végpontja erre a tengelyre esne, vagyis vagy az AD oldal, vagy a BC oldal felezőpontjával egyezne meg. Ez azonban nem osztópont, hiszen 205 páratlan szám.

Végül megmutatjuk, hogy a golyó a C csúcsnál sem tűnhet el. Ekkor ugyanis a golyó útja szimmetrikus lenne az asztal középpontjára nézve, ami csak úgy lehet, ha a szakaszok száma páratlan és a középső szakasz áthalad az asztal középpontján. Ez azonban nem lehetséges, hiszen az asztal középpontján áthaladó, az asztal oldalaival 45^o-os szöget bezáró két egyenes az asztal BC és DA oldalait nem osztópontokban metszi, hanem a csúcsoktól 27,5 cm távolságban.

Nincs mese, a golyó néhány visszapattanás után a B csúcsnál lévő lyukban fog eltűnni.

B. 3489. Bizonyítsuk be, hogy

$\displaystyle 2^n\mid{2n\choose0}+{2n\choose2}3+\dots+{2n\choose2i}3^i+\dots+{2n\choose2n}3^n.$

(5 pont)

Megoldás. A binomiális tétel alapján felírható a következő azonosság:

$\displaystyle (a+b)^n+(a-b)^n=2\sum_{0\le i\le n/2}{n\choose2i}b^{2i}a^{n-2i}\ .$

Ennek alapján a feladatban szereplő összeg így alakítható:

$\displaystyle \sum_{i=0}^n{2n\choose2i}3^i={1\over2}((1+\sqrt{3})^{2n}+(1-\sqrt{3})^{2n})={1\over2}((4+2\sqrt{3})^n+(4-2\sqrt{3})^n)=$

$\displaystyle =2^{n-1}((2+\sqrt{3})^n+(2-\sqrt{3})^n)=2^n\sum_{0\le i\le n/2}{n\choose2i}3^{i}2^{n-2i}\ ,$

ahonnan az állítás közvetlenül leolvasható.

B. 3490. A Bergengóc Országgyűlés 100 képviselője a Parlament nagytermének 10 padsorában 10 oszlopban foglal helyet. A küldötteknek mind különböző a fizetése. Minden képviselő megkérdezi szomszédait (a maga mellett, előtt, mögött ülőket és az átlós szomszédait is, összesen tehát legfeljebb 8-at), hogy mennyi a fizetésük. A küldöttek meglehetősen irigyek: csak azok elégedettek a bérükkel, akiknek legfeljebb egy olyan szomszédja van, aki többet keres náluk. Legfeljebb hány olyan képviselő lehet a Parlamentben, aki meg van elégedve a fizetésével? (4 pont)

Kvant

Megoldás. Képzeljük el a parlament nagytermét úgy, mint egy 10x10-es táblázatot. Könynyen látható, hogy a táblázat bármely 2x2-es részén helyet foglaló négy képviselő közül legfeljebb kettő lehet elégedett a fizetésével. Mivel a 10x10-es táblázat felosztható 25 darab 2x2-es részre, melyek mindegyikében legfeljebb két olyan képviselő lehet, aki meg van elégedve a fizetésével, az egész parlamentben legfeljebb 50 ilyen képviselő lehet.

Ennél többet azonban nem állíthatunk. Ha ugyanis a páros sorszámú sorokban ülő képviselőknek mind alacsonyabb a fizetésük, mint a páratlan sorszámú sorokban ülőknek, továbbá minden páratlan sorszámú sorban az ott helyet foglaló képviselőknek balról jobbra haladva csökken a fizetésük, akkor pontosan 50 olyan képviselő akad, aki elégedett a fizetésével.

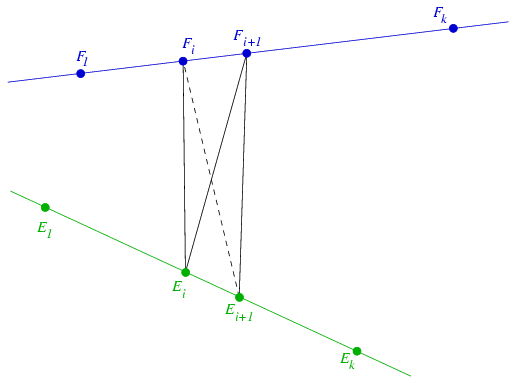
B. 3491. Döntsük el, hogy igaz-e a következő állítás. Ha adott a térben n piros pont, akkor mindig elhelyezhető 3n kék pont úgy, hogy a piros pontok által meghatározott minden tetraéder belsejében van legalább egy kék. (5 pont)

Füredi Zoltán ötletéből

Megoldás. Az állítás nem igaz. Tekintsük ugyanis a következő konstrukciót. Legyen e és f két kitérő egyenes, E₁,E₂,...,E_k és F₁,F₂,...,F_k pedig a megadott sorrendben elhelyezkedő pontok az e, illetve f egyenesen. Könnyen meggyőződhetünk arról, hogy 1$\displaystyle le$i,j$\displaystyle le$k-1 esetén az E_iE_i+1F_jF_j+1 tetraéderek közül semelyik kettőnek nincs közös belső pontja. Legyen ugyanis E_iE_i+1F_jF_j+1 és E_i'E_i'+1F_j'F_j'+1 két ilyen tetraéder, és az egyszerűség kedvéért tegyük fel, hogy i$\displaystyle ne$i', mondjuk i<i'. Ekkor az E_i+1 pontra és az f egyenesre illeszkedő síknak a két tetraéder csúcsai különböző oldalára esnek azzal a megjegyzéssel, hogy némely csúcs magán a síkon helyezkedik el. Mindenesetre az említett sík elválasztja egymástól a két tetraéder belső pontjait. Ha most n=2k$\displaystyle ge$16 és a fenti n pontot tekintjük a piros pontoknak, akkor k²-8k+1=(k-4)²-15>0 miatt 3n=6k<(k-1)², ezért bárhogyan is jelölünk ki 3n kék pontot, a fent említett (k-1)² piros csúcsú tetraéder közül legalább egynek a belseje nem tartalmazhat a kék pontok közül egyet sem.

Már regisztráltál?
Új vendég vagy?