Fizikából kitűzött gyakorlatok és feladatok
2001. október

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 227. Egy ,,szögre akasztott'' karika többféle lengést végezhet. Válasszunk ki ezek közül két jellegzeteset: azt, amikor a karika a saját síkjában leng, és azt, amikor erre merőlegesen. Mérjük meg a kétféle lengésidőt, és számítsuk ki ebből a két lengésidő arányát! Becsüljük meg a kapott eredmény hibáját! (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3456. Egymással párhuzamosan fut egy vasúti sínpár, egy autópálya és egy kerékpárút. A középen levő autópályától 600 m távolságra van a vasút és 800 m-re a kerékpárút. A vonat sebessége 90 km/h, az autóé 60 km/h. Mindhárom jármű azonos irányban halad állandó sebességgel úgy, hogy az egyik pillanatban egy egyenesre illeszkednek. Mekkora a kerékpáros sebessége, ha ez az állapot fennmarad? (4 pont)

Közli: Simon Péter, Pécs

P. 3457. Egy edény színültig van víznél nagyobb sűrűségű, vízzel nem elegyedő, 0 C^o-os folyadékkal, benne úszik egy 0 C^o-os jégdarab. A hőmérsékletet 0 C^o-on tartva, a jégdarabot infravörös fénnyel megvilágítva elolvasztjuk. Kicsordul-e a víz a pohárból? (3 pont)

Közli: Varga István, Békéscsaba

P. 3458. Mi a magyarázata annak, hogy ha egy farönkre nehéz teherrel súlyosbított balta élét illesztjük, alig-alig sérül meg a rönk, viszont ha a teher nélküli baltát felemeljük, és úgy sújtunk a rönkre, az széthasad? (3 pont)

Arisztotelész feladata nyomán

(,,Gondolatébresztő feladat'' a Sulineten)

P. 3459. Vízszintes felületen lévő m₁=0,6 kg tömegű és m₂=0,4 kg tömegű hasábokat könnyű, laza fonál köt össze. Az m₁ tömegű testet F=3 N nagyságú vízszintes erővel kezdjük húzni, és figyeljük a testek gyorsulását. A kísérletet több, különböző súrlódású felületen elvégezzük. A csúszási és a tapadási súrlódási együtthatót azonosnak tekintve \(\displaystyle mu\) nullától 0,9-ig mindenféle értéket felvehet.

a) Adjuk meg és ábrázoljuk a testek gyorsulását függvényében!

b) Határozzuk meg és ábrázoljuk a fonálban fellépő erőnek a súrlódási tényezőtől való függését! (5 pont)

Közli: Kotek László, Pécs

P. 3460.  Egy lövedék sebességének meghatározására a h=0,8 m magas asztal szélére M=1,2 kg tömegű fakockát helyezünk, amelybe vízszintes irányból m=20 g tömegű lövedéket lövünk. (A lövedék benne marad a fakockában.) Az ütközés hatására a kocka lerepül az asztalról, és x=3 m távolságban ér talajt. Mekkora volt a lövedék sebessége? (4 pont)

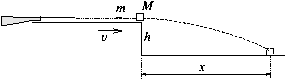
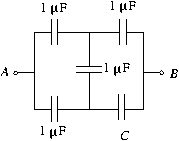
P. 3461. Az ábrán vázolt kapcsolásban C helyére tetszőleges nagyságú kondenzátort tehetünk. Milyen határok között változtatható ezáltal az A és B pontok közötti kapacitás? (5 pont)

Közli: Légrádi Imre, Sopron

P. 3462.  Ugyanakkora elektromotoros erejű és egyaránt 3 \(\displaystyle Omega\) belső ellenállású telepeket kapcsoltunk először párhuzamosan, majd sorosan egy 129 \(\displaystyle Omega\)-os fogyasztóra. Azt tapasztaltuk, hogy a soros kapcsolásnál egy-egy telep kapocsfeszültsége 10 %-kal kisebb, mint párhuzamos kapcsolás esetén.

a) Hány telepet használtunk?

b) Melyik esetben volt nagyobb a fogyasztón a teljesítmény? (4 pont)

Közli: Sütt Dezső, Budapest

P. 3463. Egyatomos ideális gázt térfogatának hetedrészére nyomunk össze, miközben nyomása hétszeresére nő egy olyan folyamatban, amelynek képe a p--V diagramon egy egyenes szakasz. A folyamat mely szakaszán vesz fel és mely szakaszán ad le hőt a gáz? Mennyi e két szakasz hosszának aránya a p--V diagramon? (5 pont)

Közli: Fári Jánosné, Szigetvár

P. 3464. Ha egy gázt melegítünk, előbb-utóbb világítani fog. Miért? (4 pont)

Közli: Kovács Gyula, Gyömrő

P. 3465. Egy hosszú, keskeny csavarrugó annyira gyenge, hogy még saját súlya alatt is számottevően megnyúlik. Ezt a rugót egyszer az egyik végénél fogva függőlegesen lógatjuk, másszor mindkét végét tartjuk olyan távolságban, hogy a rugó az ábrán látható alakot vegye fel. Melyik esetben hosszabb a megnyúlt rugó? (6 pont)

Közli: Károlyházy Frigyes, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2001. november 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 2. A ,,SLINKY-rugó'' egy olyan rugó, melynek nyújtatlan hossza elhanyagolhatóan kicsi, jó közelítéssel követi a Hooke-törvényt, és már a saját súlya hatására is számottevően megnyúlik.

a) Milyen alakot vesz fel egy ilyen rugó, ha a végeit azonos magasságban, egymástól bizonyos távolságban rögzítjük?

b) Milyen alakú a rugó, ha azt egy űrállomáson (a súlytalanság állapotában) ugrókötélként használjuk? Útmutatás: A rugó alakja mindkét esetben egy egyszerű, a középiskolai matematika és fizika órákon is gyakran emlegetett görbével írható le.