Matematikából kitűzött gyakorlatok és feladatok
2001. október

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 640. A Gergely naptár szerint 400 egymást követő év során összesen 97 szökőnapot kell beiktatni. Hány év elteltével lesz 1 nap eltérés a Gergely naptár és a ,,pontos'' naptár között, ha egy év hossza 365 nap 5 óra 48 perc 46 másodperc?

C. 641. Egy téglalap alakú papírlapot az átlója mentén összehajtunk. A dupla rétegen túlnyúló részeket levágva, a megmaradt papír széthajtás után rombusz alakú lesz. Ezt most a középvonala mentén hajtjuk össze, és a papírt az előbbihez hasonlóan megint körbenyírjuk. Milyen téglalapból induljunk ki, hogy a végül megmaradt papír széthajtás után szabályos hatszög alakú legyen?

C. 642. Egy természetes szám négyzetének utolsó két jegyét felcserélve az eggyel nagyobb szám négyzetét kapjuk. Határozzuk meg az összes ilyen számot.

Javasolta: Fried Ervin, Budapest

C. 643. Az ABC háromszög területe t, kerülete k, a körülírt kör sugara R. Bizonyítsuk be, hogy \(\displaystyle 4tR\le\left({k\over3}\right)^3\).

C. 644. Egy háromszög szögei , és . Bizonyítsuk be, hogy:

\(\displaystyle {\cos\alpha\over\sin\beta\sin\gamma}+{\cos\beta\over\sin\alpha\sin\gamma}+{\cos\gamma\over\sin\alpha\sin\beta}=2.\)

Javasolta: José Luis Díaz, Barcelona

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3482. Négy jóbarát észrevette, hogy ha elosztják a könyveik számát a számjegyek összegével, akkor eredményül mind a négyen ugyanazt az egész számot, 13-at kapják. Bizonyítsuk be, hogy legalább kettejüknek ugyanannyi könyve van. (4 pont)

Javasolta: Gerőcs László, Budapest

B. 3483. Az ABCD téglalap AB oldalának felezőpontja F. A C-ből induló szögfelező egy P pontjának vetülete a BC egyenesre Q. Bizonyítsuk be, hogy ha a PF egyenes merőleges a DQ egyenesre, akkor AP=BC. (3 pont)

B. 3484. Egy háromszög , , szögeire 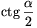, \(\displaystyle \ctg{\beta\over2}\), 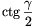egymást követő egész számok. Mekkora a háromszög legnagyobb szöge? (3 pont)

B. 3485. Az A halmaz elemei pozitív egész számok, és tetszőleges x, y\(\displaystyle in\)A, x>y esetén 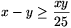. Legfeljebb hány eleme lehet az A halmaznak? (4 pont)

Vojtech Jarnik matematikaverseny, Ostrava, 2001

B. 3486. Adott a síkon 2001 pont és egy egységnyi sugarú körvonal. Bizonyítsuk be, hogy található a körvonalon olyan pont, amelytől az adott pontokig mért távolságok összege legalább 2001. (4 pont)

Nemzetközi Magyar Matematika Verseny, 2001

B. 3487. Határozzuk meg mindazokat a pozitív valós számok halmazán értelmezett f függvényeket, amelyek az értelmezési tartományukban mindenütt eleget tesznek az 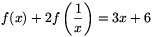összefüggésnek. (3 pont)

B. 3488. Egy téglalap alakú ABCD biliárdasztal oldalai AB=150 cm, BC=205 cm. Az asztalon négy lyuk van, ezek a csúcsokban találhatók. Az A csúcsból (a lyuk felől) ellökünk egy golyót az asztal oldalával 45^o-os szöget bezáró irányban. Valahányszor az asztal széléhez ér, a golyó rugalmasan visszapattan. Mi történik a golyóval? (4 pont)

B. 3489. Bizonyítsuk be, hogy

\(\displaystyle 2^n\mid{2n\choose0}+{2n\choose2}3+\dots+{2n\choose2i}3^i+\dots+{2n\choose2n}3^n.\)

(5 pont)

B. 3490. A Bergengóc Országgyűlés 100 képviselője a Parlament nagytermének 10 padsorában 10 oszlopban foglal helyet. A küldötteknek mind különböző a fizetése. Minden képviselő megkérdezi szomszédait (a maga mellett, előtt, mögött ülőket és az átlós szomszédait is, összesen tehát legfeljebb 8-at), hogy mennyi a fizetésük. A küldöttek meglehetősen irigyek: csak azok elégedettek a bérükkel, akiknek legfeljebb egy olyan szomszédja van, aki többet keres náluk. Legfeljebb hány olyan képviselő lehet a Parlamentben, aki meg van elégedve a fizetésével? (4 pont)

Kvant

B. 3491. Döntsük el, hogy igaz-e a következő állítás. Ha adott a térben n piros pont, akkor mindig elhelyezhető 3n kék pont úgy, hogy a piros pontok által meghatározott minden tetraéder belsejében van legalább egy kék. (5 pont)

Füredi Zoltán ötletéből

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 272. A Bergengóc Országgyűlés 100 képviselője a Parlament nagytermének 10 padsorában 10 oszlopban foglal helyet. A küldötteknek mind különböző a fizetése. Minden képviselő megkérdezi szomszédait (a maga mellett, előtt és mögött ülőket, összesen tehát legfeljebb 4-et), hogy mennyi a fizetésük. A küldöttek meglehetősen irigyek: csak azok elégedettek a bérükkel, akiknek legfeljebb egy olyan szomszédja van, aki többet keres náluk. Legfeljebb hány olyan képviselő lehet a Parlamentben, aki meg van elégedve a fizetésével?

A Kvant nyomán

A. 273. Szerkesszük meg az ABC háromszöget, amelynek beírt köre az AB, BC, CA oldalakat rendre a C₁, A₁, B₁ pontokban érinti, ha adott az A csúcs, az A₁B₁ egyenes és a B₁C₁ szakasz felezőpontját a B csúccsal összekötő egyenes.

Javasolta: Kálmán Tamás, Budapest

A. 274. Legyenek a, b, c olyan pozitív egészek, amelyekre ac=b²+b+1. Bizonyítsuk be, hogy az

ax²-(2b+1)xy+cy²=1

egyenletnek létezik egész megoldása.

Lengyel versenyfeladat

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2001. november 15.