A számítástechnika-versenyben kitűzött feladatok 2001. november

Kérjük, olvassa el a versenykiírást.

I. 7. A Faktoriális(N) függvény rendkívül gyorsan növekszik. Míg az 5!=120, addig már a 10!=3 628 800 ábrázolásához 4 byte-os egész számokra van szükség. A 100! pedig már csak speciális matematikai programokkal kezelhető.

Tudjuk azonban, hogy minden természetes számnak elkészíthető a prímtényezős felbontása. Például:

5!=2^3.3^.5      10!=2^8.3^4.5^2.7.

Készítsünk programot, amely beolvassa billentyűzetről N értékét (1N10 000), majd kiírja a képernyőre az N! prímtényezős felbontását. (10 pont)

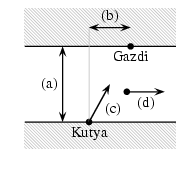
I. 8. Egy kutya úgy úszik át a folyón a túlparton álló gazdájához, hogy minden pillanatban a gazdi irányába igyekszik. Ezt a mozgást kell közelítő módszerrel modellezni, és a képernyőre kirajzolnod. Ehhez a következő, valós értékű paramétereket kell beolvasnia a programnak a billentyűzetről:

(a) A folyó szélességét méterben.

(b) A gazda távolságát méterben a kutya kezdőpontjának vetületétől a túlparton (pozitív, ha a folyásiránnyal azonos irányban van, negatív az ellenkező esetben).

(c) A kutya sebességét (m/s, nagysága állandó).

(d) A folyó sebességét (m/s, a folyó minden pontjában állandó nagyságú).

(e) A közelítés pontosságát, azaz annak az időintervallumnak a hosszát másodpercekben, amelyen belül a program egyenes vonalú mozgással számolhat.

A folyó két partját párhuzamos egyeneseknek tekintjük. A modellezés akkor álljon le, amikor a kutya már egy méternél közelebb kerül a túlsó parthoz.

Rajzoljuk ki a két partot jelző vízszintes egyeneseket, a kutya és a gazda kezdőhelyzetét és a kutya útját. (10 pont)

I. 9. A binomiális együtthatók szokásos elrendezése (Pascal háromszög) az ábrán látható alakú lehet. A szélső elemek kivételével mindegyikre igaz, hogy a fölötte levő és az attól eggyel balra levő elem összege.

Készítsünk Excel táblázatot, amely ilyen módon képes megadni a Pascal háromszög első N+1 sorát! Az első sor hetedik cellájába lehessen beírni N értékét (1N20), és a táblázat minden esetben pontosan N+1 sorból álljon! (10 pont)

A számítástechnika feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2001. december 13.