 |
A 2001. decemberi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 278. A P pont az ABCD téglalap
AC átlójának C-n túli meghosszabbításán helyezkedik el
úgy, hogy BPD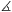 =CBP
=CBP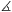 . Határozzuk meg a PB:PC arányt.
. Határozzuk meg a PB:PC arányt.
1. megoldás. Legyen P merőleges vetülete a CD
és AB egyenesekre Q, illetve R, PAR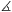 =PCQ
=PCQ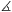 =
= és BPD
és BPD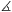 =CBP
=CBP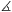 =BPR
=BPR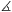 =
=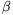 . Válasszuk a
PC szakasz hosszát egységnyinek, a PB szakasz hossza
legyen x. A feladat x meghatározása.
. Válasszuk a
PC szakasz hosszát egységnyinek, a PB szakasz hossza
legyen x. A feladat x meghatározása.
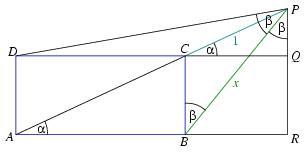
Például a PCQ és PBR derékszögű háromszögekből és a
CBRQ téglalapból xsin\(\displaystyle beta\)=BR=CQ=cos , azaz
, azaz 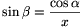 .
.
A PDQ, PCQ, PAR és PBR háromszögekből és az ARQD téglalapból
\(\displaystyle \tg2\beta={DQ\over PQ}={AR\over\sin\alpha}={PR\cdot\ctg\alpha\over\sin\alpha}={x\cdot\cos\beta\cdot\ctg\alpha\over\sin\alpha}=x\cdot\cos\beta\cdot{\cos\alpha\over\sin^2\alpha}.\)
Átrendezve és behelyettesítve a \(\displaystyle \sin\beta={\cos\alpha\over x}\) összefüggést,
\(\displaystyle {x\cdot\cos\alpha\over\sin^2\alpha}={\tg2\beta\over\cos\beta}={2\sin\beta\over1-2\sin^2\beta}={2{\cos\alpha\over x}\over1-2{\cos^2\alpha\over x^2}},\)
amiből x2=2sin2 +2cos2\(\displaystyle alpha\)=2, azaz
+2cos2\(\displaystyle alpha\)=2, azaz 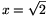 .
.
A PB:PC arány tehát az \(\displaystyle alpha\) szögtől függetlenül mindig 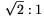 .
.
2. megoldás. Elemi bizonyítást adunk arra, hogy 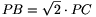 . Legyen S a BC és a PD egyenes
metszéspontja; a feltételek szerint a BPS háromszög egyenlő
szárú. Legyen R a PB egyenesnek S-sel megegyező
oldalán az a pont, amelyre a PBR háromszög egyenlő szárú és
derékszögű, azaz BR=PR és PRB
. Legyen S a BC és a PD egyenes
metszéspontja; a feltételek szerint a BPS háromszög egyenlő
szárú. Legyen R a PB egyenesnek S-sel megegyező
oldalán az a pont, amelyre a PBR háromszög egyenlő szárú és
derékszögű, azaz BR=PR és PRB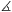 =90o. Az R és az S pont is a
PB szakasz felező merőlegesén van.
=90o. Az R és az S pont is a
PB szakasz felező merőlegesén van.
Legyen továbbá T az ABCD téglalap köré írt kör és a PD egyenes metszéspontja. A körnek BD az egyik átmérője, ezért a BT szakasz merőleges a PD egyenesre.
Mivel ACTD húrnégyszög, PTC\(\displaystyle szög\)=PAD\(\displaystyle szög\)=PCS\(\displaystyle szög\). A PCS és PTC háromszögek szögei megegyeznek, a két háromszög tehát hasonló, és PC:PS=PT:PC, átrendezve PC2=PS.PT.
Mivel PRB\(\displaystyle szög\)=PTB\(\displaystyle szög\)=90o, a PRTB négyszög is húrnégyszög, és RTP\(\displaystyle szög\)=RBP\(\displaystyle szög\)=PRS\(\displaystyle szög\). A PRS és PTR háromszögek is hasonlóak, ebből az előbbiekhez hasonlóan kapjuk, hogy PR2=PS.PT.
Azt kaptuk, hogy PC2=PR2=PS.PT, vagyis PC=PR és így \(\displaystyle PB:PC=PB:PR=\sqrt2:1\).
A. 279. Léteznek-e olyan f és g racionális tört függvények, amelyekre
(f(x))3+(g(x))3=x?
Megoldás. Bebizonyítjuk, hogy sem a valós, sem a komplex együtthatós racionális törtfüggvények körében nincsenek megoldásai a függvényegyenletnek.
Tegyük fel, hogy az állításunkkal ellentétben mégis van megoldás. Legyen az f(x) és a g(x) nevezőjének szorzata a c(x) polinom, ekkor f(x)=a(x)/c(x) és g(x)=b(x)/c(x) alkalmas a és b polinomokkal. Ezeket behelyettesítve (1)-be,
| (2) | a3(x)+b3(x)=x.c3(x). |
Tekintsük a (2) egyenletnek egy olyan megoldását, amelyben
c(x) nem 0 és a foka minimális. Legyen 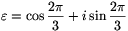 az első harmadik
egységgyök. A (2) baloldala szorzattá alakítható:
az első harmadik
egységgyök. A (2) baloldala szorzattá alakítható:
| (3) | (a(x)+b(x)).(a(x)+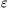 b(x)).(a(x)+ b(x)).(a(x)+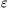 2b(x))=x.c3(x). 2b(x))=x.c3(x). |
Azt állítjuk, hogy a baloldalon álló három tényező páronként
relatív prím. Ezt az eslő két tényezőre mutatjuk meg, a többi pár
esetében ugyanígy történik. Tegyük fel, hogy az
a(x)+b(x) és a(x)+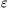 b(x) polinomoknak van egy legalább
elsőfokú közös osztója: d(x). Ekkor d(x)
osztója az \(\displaystyle {1\over1-\varepsilon}\big((a(x)+b(x))-(a(x)+\varepsilon
b(x))\big)=b(x)\) polinomnak is és hasonlóképpen
a(x)-nek is. A (2) baloldala és ezáltal
x.c3(x) is osztható
d3(x)-szel, vagyis c(x)
osztható d(x)-szel. Ekkor viszont az a(x),
b(x), c(x) polinomokat
d(x)-szel osztva egy olyan megoldást kapunk, amelyben
c foka kisebb. Az a(x)+b(x) és
a(x)+\(\displaystyle varepsilon\)b(x) polinomoknak
tehát nem lehet legalább elsőfokú közös osztójuk, relatív prímek.
b(x) polinomoknak van egy legalább
elsőfokú közös osztója: d(x). Ekkor d(x)
osztója az \(\displaystyle {1\over1-\varepsilon}\big((a(x)+b(x))-(a(x)+\varepsilon
b(x))\big)=b(x)\) polinomnak is és hasonlóképpen
a(x)-nek is. A (2) baloldala és ezáltal
x.c3(x) is osztható
d3(x)-szel, vagyis c(x)
osztható d(x)-szel. Ekkor viszont az a(x),
b(x), c(x) polinomokat
d(x)-szel osztva egy olyan megoldást kapunk, amelyben
c foka kisebb. Az a(x)+b(x) és
a(x)+\(\displaystyle varepsilon\)b(x) polinomoknak
tehát nem lehet legalább elsőfokú közös osztójuk, relatív prímek.
Három, páronként relatív prím polinom szorzata csak úgy lehet
x.c3(x) alakó, ha közülük
kettő teljes köb, egy pedig egy teljes köb x-szerese. Mivel az
egyenlet szimmetrikus a b(x), 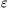 b(x),
b(x), 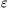 2b(x) polinomokra,
feltételezhetjük, hogy az első tényező a teljes köb x-szerese,
azaz alkalmas u(x), v(x),
w(x) polinomokkal
2b(x) polinomokra,
feltételezhetjük, hogy az első tényező a teljes köb x-szerese,
azaz alkalmas u(x), v(x),
w(x) polinomokkal
a(x)+b(x)=x.u3(x),
a(x)+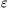 b(x)=v3(x),
b(x)=v3(x),
a(x)+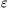 2b(x)=w3(x),
2b(x)=w3(x),
és
c(x)=u(x)v(x)w(x).
Mint könnyen ellenőrizhető,
| (4) | (1+\(\displaystyle varepsilon\)2)(a(x)+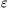 b(x))+(1+ b(x))+(1+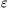 )(a(x)+ )(a(x)+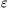 2b(x))=a(x)+b(x). 2b(x))=a(x)+b(x). |
A baloldalon mindkét tag teljes köb:
(1+\(\displaystyle varepsilon\)2)(a(x)+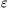 b(x))=d3(x)
b(x))=d3(x)
és
(1+\(\displaystyle varepsilon\))(a(x)+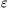 2b(x))=e3(x)
2b(x))=e3(x)
alkalmas d(x) és e(x) polinomokkal. Ezeket behelyettesítve (4)-be,
d3(x)+e3(x)=x.u3(x).
A d(x), e(x), u(x) polinomok tehát egy újabb megoldását adják a (2) egyenletnek. Ha u(x) foka kisebb, mint c(x) foka, az ellentmondás, mert feltételeztük, hogy c(x) foka minimális. Ha viszont u(x) foka nem kisebb, mint c(x)=u(x)v(x)w(x) foka, az csak úgy lehetséges, ha v(x) és w(x) konstans. Ekkor viszont az a(x) és b(x) polinom is konstans, (2) baloldalán egy konstans áll, a joboldalán pedig egy legalább elsőfokú polinom. Ez szintén ellentmondás.
A. 280. Tetszőleges n pozitív egész számra legyen
fn(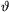 )=sin
)=sin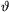 .sin(2
.sin(2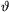 ).sin(4
).sin(4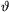 ).....sin(2n
).....sin(2n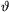 ).
).
Bizonyítsuk be, hogy tetszőleges 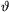 valós szám és n pozitív egész
esetén
valós szám és n pozitív egész
esetén
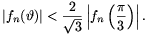
IMC 8, Prága, 2001
Megoldás. Megengedjük az n=0 esetet is, ekkor értelemszerűen f0(\(\displaystyle vartheta\))=sin\(\displaystyle vartheta\).
Mint könnyen ellenőrizhető, (5) jobboldalán 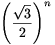 áll, tehát a bizonyítandó
állítás:
áll, tehát a bizonyítandó
állítás:
| (6) | 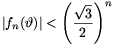 |
Az állítást teljes indukcióval igazoljuk. Az n=1 és n=2 esetekben az állítás triviális:
\(\displaystyle |\sin\vartheta|<{2\over\sqrt3},\)
illetve
|sin\(\displaystyle vartheta\).sin2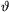 |<1.
|<1.
Legyen tehát n>3, és tegyük fel, hogy minden kisebb értékre az állítás igaz. Ha \(\displaystyle |\sin\vartheta|\le{\sqrt3\over2}\), akkor az indukciós feltevés értelmében
\(\displaystyle |f_n(\vartheta)|=|\sin\vartheta|\cdot|f_{n-1}(2\vartheta)|<{\sqrt3\over2}\cdot\left({\sqrt3\over2}\right)^{n-1}=\left({\sqrt3\over2}\right)^n.\)
Ha \(\displaystyle |\sin\vartheta\){\sqrt3\over2}|">, akkor 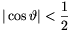 ,
,
\(\displaystyle |\sin\vartheta\cdot\sin2\vartheta|={1\over2}|\cos\vartheta-\cos3\vartheta|<{1\over2}\left({1\over2}+1\right)={3\over4},\)
és
\(\displaystyle |f_n(\vartheta)|=|\sin\vartheta\cdot\sin2\vartheta|\cdot|f_{n-2}(2\vartheta)|<{3\over4}\cdot\left({\sqrt3\over2}\right)^{n-2}=\left({\sqrt3\over2}\right)^n.\)

