A 2001. decemberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3478. Becsüld meg, mekkora munkát végzel, miközben fekvésből szabályos fekvőtámasz-helyzetbe nyomod ki magadat! (3 pont)

Károly Ireneusz verseny, Szombathely

Megoldás. Egy diák a saját tömegét mondjuk 50 kg-nak méri, a súlya 500 N. A karja kinyújtásakor a válla kb. 50 cm-nyit emelkedik, de a tömegközéppontja (amely nagyjából a köldöke magasságában van) csupán 0,3 m-rel kerül magasabbra. A végzett mechanikai munka a gravitációs helyzeti energia változásával egyenlő, tehát kb. 150 J. Más súlyú és magasságú (középiskolás korú) fiatalnál a fekvőtámasz során végzett munkát hozzávetőlegesen 100 és 200 J közötti értékűnek becsülhetjük.

P. 3479. Egy csövön keresztül hidrogéngázt áramoltatnak, miközben a csövet körülvevő vízzel hűtik a gázt. A beáramló gáz hőmérséklete 60 C^o, a kiáramlóé 30 C^o. A hűtőtartályban 60 liter víz fér el, amit óránként cserélnek. A hűtővíz kezdeti hőmérséklete 10 C^o, amikor pedig cserélik, 20 C^o. Hány kg gáz áramlik át a csövön egy óra alatt? (4 pont)

,,Keresd a megoldást'' verseny, Szeged

Megoldás. Feltételezzük, hogy a gáz nyomása az áramlás során nem változik számottevően. (Ez szigorúan véve biztosan nem igaz, de a hőcserélő technikai megvalósításától függően jó közelítés lehet.) A gáz által leadott és a víz által felvett hő egyenlőségéből

m_v^.c_v^.T_v=m_h^.c_(p)h^.T_h,

ahonnan a hidrogén tömege

$\displaystyle m_{\rm h}={60\cdot4{,}18\cdot10\over14{,}2\cdot30}~{\rm kg}=5{,}9~{\rm kg}.$

Megjegyzés: A gáz és a folyadék közötti hőcsere sebessége függ a hőmérsékletük különbségétől, jó közelítéssel arányos azzal. Ha a hűtőfolyadékot nem folyamatosan cserélik, hanem a feladatban leírt módon (szakaszosan), akkor a be- és kiáramló gáz hőmérsékletkülönbsége csak úgy lehet időben állandó, ha a gáz áramlási sebessége a hűtővíz lecserélése előtt kisebb, mint a csere után. Ezt (a gáz áramlási sebességének periodikus változtatását) technikailag nehéz lenne megoldani, ehelyett inkább a hűtővíz folyamatos cserélésének módszerét alkalmazzák.

P. 3480. Egy bolygón, amelynek sugara 5000 km, kilőnek egy rakétát az első kozmikus sebességgel, a függőlegeshez képest 60^o-os szögben. Legfeljebb milyen magasra ér fel a rakéta? (5 pont)

Schwartz-emlékverseny, Nagyvárad (Románia)

Megoldás. Az energia- és perdületmegmaradás törvénye alapján a függőlegessel $\displaystyle alpha$ szögben éppen az első kozmikus sebességgel elindított rakéta emelkedési magassága h=Rcos, a megadott számadatokkal h=2500 km. (A bolygó forgását nem vettük figyelembe.)

P. 3481. Hogyan függ a hőmérséklettől egy homogén anyagból készült fizikai inga lengésideje? (4 pont)

Közli: Horváth István, Fonyód

Megoldás. A fizikai inga lengésideje

$\displaystyle T=2\pi\sqrt{\Theta\over mgs},$

ahol $\displaystyle \Theta$ az inga $\displaystyle ell$ lineáris méretének négyzetével, az s távolság pedig $\displaystyle ell$-lel egyenesen arányos. Így $\displaystyle T\propto\ell^{1/2}$.

A t hőmérséklet $\displaystyle Delta$t megváltozásakor a relatív hosszváltozás

$\displaystyle {\Delta\ell\over\ell}=\alpha\Delta t,$

ahol $\displaystyle alpha$ a hőtágulási együttható. A lengésidő relatív megváltozása ezek szerint

$\displaystyle {\Delta T\over T}={1\over2}\alpha\Delta t.$

P. 3482. Három koncentrikus, vékony fémgömbhéj közül az R sugarú középső gömbhéjon Q töltés van, az $\displaystyle R_{\rm b}={1\over2}R$ sugarú belső és az $\displaystyle R_{\rm k}={3\over2}R$ sugarú külső gömbhéjat leföldeltük.

a) Mekkora töltés van a földelt gömbhéjakon?

b) Ábrázoljuk a térerősséget a középponttól mért távolság függvényében! (5 pont)

Közli: Kotek László, Pécs

Megoldás. Jelöljük a belső gömbhéj töltését Q_b-vel, a külső gömbét pedig Q_k-val! Mivel egy q töltésű, a sugarú gömbhéj potenciálja a gömbhéjon belül kq/a, a gömbhéjon kívül (r>a esetén) pedig kq/r, és a három gömbhéj potenciáljai algebrailag összegezhetők, a földelt belső és külső gömb akkor lesz nulla potenciálon, ha fennáll:

$\displaystyle k{Q_{\rm b}\over{1\over2}R}+k{Q\over R}+k{Q_{\rm k}\over{3\over2}R}=0,$

illetve

$\displaystyle k{Q_{\rm b}\over{3\over2}R}+k{Q\over{3\over2}R}+k{Q_{\rm k}\over{3\over2}R}=0.$

Ezekből az egyenletekből a kérdéses töltések kiszámíthatók:  $\displaystyle Q_{\rm b}=-{1\over4}Q$

, valamint $\displaystyle Q_{\rm k}=-{3\over4}Q$.

Ugyanezt az eredményt úgy is megkaphatjuk, hogy a külső és a középső, valamint a középső és a belső gömbhéjat egy-egy párhuzamosan kapcsolt gömbkondenzátornak tekintjük. Ezek kapacitásának aránya 3:1, a külső gömbhéjon tehát háromszor akkora töltésnek kell lennie, mint a belsőn. Másrészt a rendszer össztöltése nulla kell legyen, hiszen a külső gömb (és az $\displaystyle${3\over2}R"> koordinátájú pontok) potenciálja nulla.

Az elektromos térerősség sugár irányú, előjeles ,,nagysága'' pedig

\(\displaystyle E(r)=\cases{-k{\displaystyle1\over\displaystyle4}{\displaystyle Q\over\displaystyle r^2},{\rm ha\ }{1\over2}R

P. 3483.  Az ábra szerinti kapcsolásban a K kapcsoló kezdetben nyitott és a kondenzátor töltetlen. Ezután zárjuk a kapcsolót, és hagyjuk, hogy a kondenzátor maximálisan feltöltődjön, majd nyitjuk a kapcsolót. Határozzuk meg az ampermérő által mért értékeket

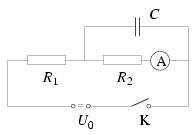
a) közvetlenül a kapcsoló zárása után;

b) a kapcsoló zárását követően hosszú idő múlva;

c) közvetlenül a kapcsoló nyitása után!

(U₀=30 V, R₁=10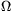 k, R₂=5 k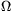.) (4 pont)

Nagy László verseny, Kazincbarcika

Megoldás. a) Kezdetben a kondenzátor töltetlen, a feszültsége tehát nulla. A kapcsoló zárását követően a kondenzátor töltése hirtelen nem tud megváltozni, a feszültsége is csak fokozatosan nő, emiatt az ampermérő közvetlenül a kapcsoló zárása után még nem jelez áramot.

b) Hosszú idő múlva a kondenzátor feltöltődik, rajta áram már nem folyik, így az ampermérő

$\displaystyle {U_0\over R_1+R_2}=2~\rm mA$

áramot jelez.

c) A kapcsoló nyitása után a kondenzátor elkezd kisülni, de közvetlenül a kapcsoló nyitása után a feszültsége még a korábbi (az egyenáramú feszültségosztásnak megfelelő) 10 V-os érték. Az R₂ ellenállásra eső feszültség tehát a kapcsoló nyitása során hirtelen nem változik meg, így az ampermérő is a korábbi 2 mA-es értéket mutatja.

P. 3484.  Mekkora legyen az ábrán látható változtatható kondenzátor kapacitása, hogy a voltmérő a legnagyobb feszültséget mutassa? (5 pont)

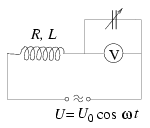
Madas László feladata nyomán

Megoldás. Az áramkörben folyó áram

$\displaystyle I={U_0\over\sqrt{R^2+\left(L\omega-{1\over\omega C}\right)^2}},$

a kondenzátorra eső feszültség pedig

$\displaystyle U_C={I\over\omega C}={U_0\over\sqrt{R^2\omega^2C^2+(1-\omega^2LC)^2}}.$

Ez akkor a legnagyobb, amikor a nevezőben a gyökjel alatt álló kifejezés a legkisebb, ami (mint az teljes négyzetté alakítással elemi úton belátható)

$\displaystyle C={1\over L\omega^2+R^2/L}$

kapacitásnál áll fenn.

Megjegyzés. A kondenzátor feszültsége nem az áramrezonanciának megfelelő L$\displaystyle omega$=1/($\displaystyle omega$C) feltétel teljesülésekor lesz a legnagyobb, hanem annál kisebb kapacitásértéknél.

P. 3485. A Nap sokkal nagyobb erővel vonzza a Földet, mint a Hold.

a) Mekkora a két erő aránya?

b) Mi a magyarázata annak, hogy a Hold árapálykeltő hatása mégis többszöröse a Napénak? (5 pont)

Közli: Honyek Gyula, Budapest

Megoldás. a) A Newton-féle gravitációs erőtörvény szerint a vonzóerő fM/r²-tel arányos, tehát a kérdéses erő-arány

$\displaystyle {F_{\rm Nap}\over F_{\rm Hold}}={M_{\rm Nap}\over M_{\rm Hold}}\cdot\left({r_{\rm Hold}\over r_{\rm F\ddot old}}\right)^2,$

ahol $\displaystyle r_{\rm F\ddot old}$ a Föld, r_Hold pedig a Hold pályájának sugara. Mivel a tömegek aránya kb. 27 millió, a pályasugaraké pedig 1:400,

$\displaystyle {F_{\rm Nap}\over F_{\rm Hold}}\approx170,$

tehát a Nap valóban sokkal nagyobb erővel vonzza a Földet, mint a Hold.

Az árapályerő nem közvetlenül a gravitációs erővel, hanem annak inhomogenitásával, távolság szerinti változási ütemével (deriváltjával) arányos:

$\displaystyle F_{\rm\acute arap\acute aly}\propto{dF(r)\over dr}\propto{M\over r^3}.$

Így

$\displaystyle {F_{\rm Nap}^{\rm\acute arap\acute aly}\over F_{\rm Hold}^{\rm\acute arap\acute aly}}={M_{\rm Nap}\over M_{\rm Hold}}\cdot\left({r_{\rm Hold}\over r_{\rm F\ddot old}}\right)^3\approx0{,}5,$

tehát árapály szempontjából a Hold hatása mintegy kétszerese a Napénak.

P. 3486. Az ¹⁴N mag kötési energiája 16,19 pJ, a ¹⁴C mag kötési energiája 16,37 pJ. Melyik atommag bomlik a másikra, és miért? (5 pont)

Szilárd Leó nukleáris verseny, Paks

A feladat megoldása április végén fog megjelenni.

P. 3487. Száz éve (1901. december 5-én) született Werner Heisenberg, Nobel-díjas német elméleti fizikus. Az általa bevezetett határozatlansági reláció alapján becsüljük meg, mekkora egy fenyőtű hegyén ,,ülő'' szénatom, illetve elektron sebességének határozatlansága! (4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. A Heisenberg-féle határozatlansági összefüggés szerint egy m tömegű részecske helyének és sebességének x, illetve $\displaystyle Delta$v határozatlansága között fennáll

$\displaystyle \Delta v\cdot\Delta x\le{h\over m},$

ahol h$\displaystyle approx$10^-34 Js a Planck-állandó. (A képlet fenti formája csak nagyságrendi tájékozódásra alkalmas, emiatt a benne szereplő számfaktorokat és a Planck-állandó pontos számértékét ki se írtuk.)

Ha egy fenyőtű átmérőjét 1 mm-esnek vesszük, s a ,,hegyének'' méretét ennek tizedére, 10^-4 m-re becsüljük, akkor a kb. 10^-30 kg tömegű elektron sebességének határozatlanságára $\displaystyle Delta$v$\displaystyle approx$1 m/s adódik. (Ez látszólag nagy értéknek tűnhet, de vegyük figyelembe, hogy az elektron hőmozgásból adódó átlagsebessége szobahőmérsékleten kb. 70 km/s.)

A szénatom tömege 5 nagyságrenddel nagyobb, mint egyetlen elektron tömege, egy fenyőtű hegyének méretére korlátozott szénatom kvantumos eredetű sebességbizonytalansága tehát csak 10^-5 m/s nagyságrendű. Még nagyobb objektumok (pl. egy porszem vagy makroszkopikus testek) esetében a Heisenberg-relációból adódó korlát teljes mértékben elhanyagolható.