Fizikából kitűzött gyakorlatok és feladatok
2001. december

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 229.  Vízszintes, sima és száraz műanyaglapon állítsunk elő (pl. szemcseppentővel) különböző tömegű vízcseppeket! Vizsgáljuk meg, hogyan függ a vízcsepp átmérője a csepp tömegétől! (6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3478. Becsüld meg, mekkora munkát végzel, miközben fekvésből szabályos fekvőtámasz-helyzetbe nyomod ki magadat! (3 pont)

Károly Ireneusz verseny, Szombathely

P. 3479. Egy csövön keresztül hidrogéngázt áramoltatnak, miközben a csövet körülvevő vízzel hűtik a gázt. A beáramló gáz hőmérséklete 60 C^o, a kiáramlóé 30 C^o. A hűtőtartályban 60 liter víz fér el, amit óránként cserélnek. A hűtővíz kezdeti hőmérséklete 10 C^o, amikor pedig cserélik, 20 C^o. Hány kg gáz áramlik át a csövön egy óra alatt? (4 pont)

,,Keresd a megoldást'' verseny, Szeged

P. 3480. Egy bolygón, amelynek sugara 5000 km, kilőnek egy rakétát az első kozmikus sebességgel, a függőlegeshez képest 60^o-os szögben. Legfeljebb milyen magasra ér fel a rakéta? (5 pont)

Schwartz-emlékverseny, Nagyvárad (Románia)

P. 3481. Hogyan függ a hőmérséklettől egy homogén anyagból készült fizikai inga lengésideje? (4 pont)

Közli: Horváth István, Fonyód

P. 3482. Három koncentrikus, vékony fémgömbhéj közül az R sugarú középső gömbhéjon Q töltés van, az \(\displaystyle R_{\rm b}={1\over2}R\) sugarú belső és az \(\displaystyle R_{\rm k}={3\over2}R\) sugarú külső gömbhéjat leföldeltük.

a) Mekkora töltés van a földelt gömbhéjakon?

b) Ábrázoljuk a térerősséget a középponttól mért távolság függvényében! (5 pont)

Közli: Kotek László, Pécs

P. 3483.  Az ábra szerinti kapcsolásban a K kapcsoló kezdetben nyitott és a kondenzátor töltetlen. Ezután zárjuk a kapcsolót, és hagyjuk, hogy a kondenzátor maximálisan feltöltődjön, majd nyitjuk a kapcsolót. Határozzuk meg az ampermérő által mért értékeket

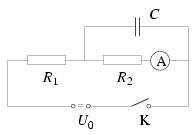
a) közvetlenül a kapcsoló zárása után;

b) a kapcsoló zárását követően hosszú idő múlva;

c) közvetlenül a kapcsoló nyitása után!

(U₀=30 V, R₁=10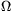 k, R₂=5 k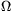.) (4 pont)

Nagy László verseny, Kazincbarcika

P. 3484.  Mekkora legyen az ábrán látható változtatható kondenzátor kapacitása, hogy a voltmérő a legnagyobb feszültséget mutassa? (5 pont)

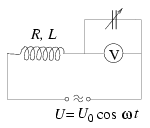
Madas László feladata nyomán

P. 3485. A Nap sokkal nagyobb erővel vonzza a Földet, mint a Hold.

a) Mekkora a két erő aránya?

b) Mi a magyarázata annak, hogy a Hold árapálykeltő hatása mégis többszöröse a Napénak? (5 pont)

Közli: Honyek Gyula, Budapest

P. 3486. Az ¹⁴N mag kötési energiája 16,19 pJ, a ¹⁴C mag kötési energiája 16,37 pJ. Melyik atommag bomlik a másikra, és miért? (5 pont)

Szilárd Leó nukleáris verseny, Paks

P. 3487. Száz éve (1901. december 5-én) született Werner Heisenberg, Nobel-díjas német elméleti fizikus. Az általa bevezetett határozatlansági reláció alapján becsüljük meg, mekkora egy fenyőtű hegyén ,,ülő'' szénatom, illetve elektron sebességének határozatlansága! (4 pont)

Közli: Radnai Gyula, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. január 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 4. Egy víztartály keresztmetszete a magasság függvényében (mondjuk hatványfüggvény szerint) változik. Milyen legyen ez a függvény, ha azt szeretnénk elérni, hogy a tartályban levő víz mennyisége a fenéken levő csap kinyitása után -- a radioaktív bomlástörvényhez hasonlóan -- időben exponenciálisan csökkenjen? Modellezzük víztartályokkal a radioaktív bomlási sorokat!

Útmutatás: xⁿ változási üteme (x szerinti deriváltja) n^.x^n-1.