Matematikából kitűzött gyakorlatok és feladatok
2001. december
Kérjük, olvassa el a versenykiírást.
 |
A C pontversenyben kitűzött gyakorlatokMinden C-jelű feladat helyes megoldásáért 5 pont jár. |
C. 650. Egy képkereskedésben a képek keretének ára egyenesen arányos a bennük lévő festmények értékével. A kereskedő annak érdekében, hogy bizonyos képek ára közötti különbséget csökkentse, felcserél egymással két-két keretet. Az egyik esetben az a kép, amely ötször annyiba került, mint a másik, kereteik felcserélése után már csak háromszor annyiba kerül. Hogyan módosul a ,,Téli táj'' és a ,,Falu rossza'' c. képek árainak aránya, ha kereteik felcserélése előtt a ,,Téli táj'' kilencszer annyiba került, mint a ,,Falu rossza''?
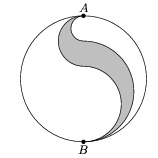
C. 651. Az ábrán látható egységnyi területű körben a szürke tartományt félkörívek határolják. Az AB átmérőnek 1/5 egységnyi része esik a satírozott tartomány belsejébe. Mekkora a satírozott tartomány kerülete és a területe?
C. 652. Legyen s páratlan sok jegyű pozitív egész szám. Jelölje f azt a számot, amely s számjegyeiből áll, csak fordított sorrendben. Bizonyítsuk be, hogy s+f pontosan akkor osztható 11-gyel, ha s is osztható 11-gyel.
C. 653. A p paraméter hány különböző értékére van az
x2-y2=0
xy+px-py=p2
egyenletrendszernek pontosan egy megoldása?
C. 654. fa, fb és fc jelölik egy a, b, c oldalú, T területű háromszög belső szögfelezőinek a hosszát. Igazoljuk, hogy
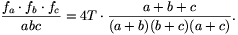
Javasolta: Kovács Gabriella, Budapest
 |
A B pontversenyben kitűzött feladatokA B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe. |
B. 3502. Az ABC hegyesszögű háromszögben az AB átmérőjű félkör a C-ből induló magasságot C1-ben, a BC átmérőjű félkör az A-ból induló magasságot A1-ben metszi. Bizonyítsuk be, hogy BC1=BA1. (3 pont)
B. 3503. Adottak az a, b, c, d és f szakaszok. Tegyük fel, hogy létezik olyan négyszög, melynek egymást követő oldalai a, b, c, d, az a és c oldalak felezőpontját összekötő szakasz hossza pedig f. Szerkesszünk ilyen négyszöget. (4 pont)
B. 3504. Jelölje S(n) a tízes számrendszerben felírt n szám jegyeinek az összegét, Uk=11...1 pedig a k darab egyessel felírt számot. Keressük meg azokat a k értékeket, amelyekre S(Uk2)=(S(Uk))2. (4 pont)
B. 3505. Egy szabályos nyolcszöget paralelogrammákra osztunk fel. Bizonyítsuk be, hogy a paralelogrammák között van téglalap. (5 pont)
B. 3506. Az f polinomra teljesül, hogy f(x2+1)-f(x2-1)=4x2+6. Határozzuk meg az f(x2+1)-f(x2) polinomot. (4 pont)
B. 3507. Legyen f(x) egész
együtthatós polinom, p és q pedig relatív prímek,
q 0. Bizonyítsuk be, hogy ha p/q gyöke az
f-nek, akkor f(k) minden k egészre
osztható p-kq-val. Igaz-e az állítás megfordítása? (4
pont)
0. Bizonyítsuk be, hogy ha p/q gyöke az
f-nek, akkor f(k) minden k egészre
osztható p-kq-val. Igaz-e az állítás megfordítása? (4
pont)
B. 3508. Az ABC és az A1B1C1 háromszögek tengelyesen tükrös helyzetűek. Húzzunk párhuzamost A1-en keresztül BC-vel, B1-en keresztül AC-vel, végül C1-en keresztül AB-vel. Bizonyítsuk be, hogy ez a három egyenes egy ponton halad át. (4 pont)
B. 3509. Bizonyítsuk be, hogy ha 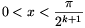 , akkor
, akkor
\(\displaystyle {1\over\sin2x}+{1\over\sin4x}+\dots+{1\over\sin2^kx}<\ctg x.\)
(3 pont)
Javasolta: Balogh János, Kaposvár
B. 3510. Az ABCD tetraéder csúcsain keresztül fektessünk a szemközti lapokkal párhuzamos síkokat. Ez a négy sík egy újabb tetraédert határoz meg. Bizonyítsuk be, hogy A, B, C és D az így kapott tetraéder lapjainak a súlypontjai. (3 pont)
B. 3511. Az a, b, c, d
nemnegatív számokra a 1, a+b
1, a+b 5, a+b+c
5, a+b+c 14 és
a+b+c+d
14 és
a+b+c+d 30. Bizonyítsuk be, hogy
30. Bizonyítsuk be, hogy 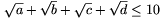 . (5 pont)
. (5 pont)
 |
Az A pontversenyben kitűzött nehezebb feladatokMinden A-jelű feladat helyes megoldásáért 5 pont jár. |
A. 278. A P pont az ABCD téglalap
AC átlójának C-n túli meghosszabbításán helyezkedik el
úgy, hogy BPD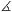 =CBP
=CBP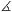 . Határozzuk meg a PB:PC arányt.
. Határozzuk meg a PB:PC arányt.
A. 279. Léteznek-e olyan f és g racionális tört függvények, amelyekre
(f(x))3+(g(x))3=x?
A. 280. Tetszőleges n pozitív egész számra legyen
fn( )=sin
)=sin .sin(2
.sin(2 ).sin(4
).sin(4 ).....sin(2n
).....sin(2n ).
).
Bizonyítsuk be, hogy tetszőleges  valós szám és n pozitív egész
esetén
valós szám és n pozitív egész
esetén
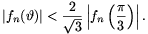
IMC 8, Prága, 2001
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
- KöMaL Szerkesztőség
Budapest 112, Pf. 32. 1518
- megoldas@komal.elte.hu (Az interneten keresztül történő
beküldésről olvassa el tájékoztatónkat)

