A 2002. januári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C.655. Barabás nagymamája egy ideje minden lottósorsoláskor félretesz perselyébe némi aprópénzt unokájának. A nagyi rendkívül precíz hölgy, és az alábbi szabályokat mindig betartja:

1) Csak fémpénzt tesz félre.

2) Egy szám kisorsolásakor a számnak megfelelő összeget teszi a perselybe, ügyelve arra, hogy a legkevesebb számú érmét használja fel.

3) A sorsolás végeztével mindig felírja, hogy melyik érméből mennyit dobott a perselybe.

Az egyik sorsolás után, ahol 7 számot sorsoltak az első 35 pozitív egész közül, nagyi azt jegyezte fel, hogy 3 db 20, 6 db 10, 5 db 5, 9 db 2 és 3 db 1 forintos érmét dobott a perselybe. Mik voltak a kisorsolt számok?

Megoldás.

Esetszétválasztás és kitartó gondolkodás után a következő megoldásra lehet jutni:

1. szám: 20+10+2+2=34

2. szám: 20+10+2+1=33

3. szám: 20+5+2+2=29

4. szám: 10+5+2+2=19

5. szám: 10+5+2+1=18

6. szám: 10+5+2=17

7. szám: 10+5+1=16

C.656. Egy 21 250 Ft-os kabát árát leszállították egy engedményes vásár alkalmából. Majd a karácsonyi vásárban akciós áron még olcsóbb, 19 176 Ft lett. Hány százalékosak az engedmények, ha tudjuk, hogy mindkettő egyjegyű szám?

Megoldás.

Legyen az egyik árengedmény a%-os, a másik pedig b%-os. Ekkor 0,9a^.09b=0,9024, vagy másképp (90+a)(90+b)=9024. Ebből 924=90(a+b)+ab. Ebből rögtön következik, hogy ab 4-re végződik. Másrészt mivel ab$\displaystyle le$81, ezért 90(a+b)$\displaystyle ge$843=90^.9,3666, és így a+b$\displaystyle ge$10. Hasonlóan 924$\displaystyle ge$90(a+b) miatt a+b$\displaystyle le$10. Tehát a+b=10, és ab 4-re végződik, amiből már következik, hogy a=4 és b=6 vagy fordítva, a=6 és b=4. Tehát az egyik árleszállítás 4, a másik 6 százalékos volt.

C.657. Egy kúp és egy henger magassága is és térfogata is egyenlő. Mekkora a kúp nyílásszöge, ha a két test palástjának felszíne is megegyezik?

Megoldás.

Nyilván egyenes körkúpról van szó. Jelölje a kúp és a henger közös magasságát m, a kúp alapkörének sugarát r, a hengerét R, illetve a kúp alkotóját a, valamint a kúp nyílásszögét 2$\displaystyle alpha$. A térfogatok egyenlőségéből $\displaystyle {{r^2\pi m}\over3}=R^2\pi m$, amiből $\displaystyle r/R=\sqrt3$. A palástok területének egyenlőségéből pedig $\displaystyle pi$ra=2R$\displaystyle pi$m, amiből cos$\displaystyle alpha$=m/a=r/2R, ami az előbbiek miatt $\displaystyle {{\sqrt3}\over2}=\cos30^{\circ}$. Így 2$\displaystyle alpha$=60^o, azaz a kúp nyílásszöge 60^o.

C.658. Oldjuk meg az

$\displaystyle {1\over x}+{1\over y}={1\over z};\quad{1\over x+15}+{1\over y-6}={1\over z};\quad{1\over x+24}+{1\over y-15}={1\over z}$

egyenletrendszert.

Megoldás.

Mivel mindhárom egyenlet jobboldala 1/z, ezért a baloldalak megegyeznek. Kis átalakítással ez azt jelenti, hogy $\displaystyle {{xy}\over{x+y}}={{(x+24)(y-15)}\over{x+y+9}}={{(x+15)(y-6)}\over{x+y+9}}.$

Az első egyenletből beszorzással és némi számolással adódik, hogy y=x+30. Ezt behelyettesítve a második egyenletbe, és azt hasonlóan átalakítva a következő másodfokú egyenlethez jutunk: x²+80x+1200=0. Ebből x₁=-20, x₂=-60. Innen y₁=10, y₂=-30, végül az eredetileg első egyenlet felhasználásával z₁=20, z₂=-20. A kapott értékeket behelyettesítve az egyenletrendszerbe, kielégítik azt.

C.659.

A 0$\displaystyle le$t$\displaystyle le$ $pi$ valós paraméter mely értékei esetén nincs megoldása a sin (x+t)=1-sinx egyenletnek?

Megoldás.Az egyenletet átrendezve sin(x+t)+sinx=1, amiből 2sin(x+t/2)^.cos(t/2)=1. Amennyiben cos(t/2)=0, akkor az egyenletnek nincs megoldása. Egyébként pedig 2cos(t/2)-vel leosztva (ami csak t-től függ, tehát paraméternek tekinthető) sin(x+t/2)=1/(2cos(t/2)). Az egyenletnek pontosan akkor van megoldása, ha a jobboldal -1 és 1 közé esik, azaz -1 $le$ 1/(2cos(t/2)) $le$ 1, tehát ha -2 $le$ 1/(cos(t/2)) $le$ 2. 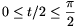Mivel 0 $le$ t $le$ $pi$ , ezért $0\leq t/2\leq{{\pi}\over2}$ , tehát cos(t/2) $ge$ 0. Így az egyenlőtlenség baloldala biztosan teljesül. A jobboldala pedig pontosan akkor, ha cos(t/2) $ge$ 1/2. 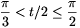Ekkor van megoldása az egyenletnek, tehát akkor nincs (cos(t/2)=0-t is beleértve), ha 0 $le$ cos(t/2)<1/2, azaz ${{\pi}\over3}<t/2\leq{{\pi}\over2}$ . Tehát akkor nincs megoldása az egyenletnek, ha ${2{\pi}\over3}<t\leq\pi.$

Már regisztráltál?
Új vendég vagy?