Matematikából kitűzött gyakorlatok és feladatok
2002. február

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 660. Hányféleképpen lehet a 8x8-as sakktábla mezői közül két különbözőt kiválasztani úgy, hogy a középpontjukat összekötő szakasz felezőpontja is egy mező középpontjába essen?

C. 661. Mi a feltétele annak, hogy egy 9-re és egy 7-re végződő egész szám szorzata 63-ra végződjön?

C. 662. Egy téglatest térfogata 8 cm³. Ha a téglatest minden élét 1 centiméterrel megnöveljük, akkor egy 27 cm³ térfogatú téglatestet kapunk. Mekkora térfogatú téglatestet kapunk, ha ismét megnöveljük az éleket 1-1 centiméterrel?

C. 663. Egy hegyesszögű háromszög alakú papírlapnak leszakadt a legnagyobb szöget tartalmazó csúcsa. A papír megmaradt részén szerkeszük meg a háromszög köré írható kör sugarát.

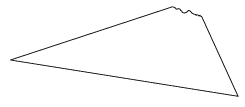
Róka Sándor (Nyíregyháza) javaslata nyomán

C. 664. Határozzuk meg az y=x²+1 és az x=y²+1 egyenletű parabolák az y=x egyenletű egyenessel párhuzamos érintőinek távolságát.

Helyesbítés

Előző számunk C. 658. gyakorlata helyesen a következő:

C. 658. Oldjuk meg az

\(\displaystyle {1\over x}+{1\over y}={1\over z};\quad{1\over x+15}+{1\over y-6}={1\over z};\quad{1\over x+24}+{1\over y-15}={1\over z}\)

egyenletrendszert.

Elnézést kérünk a hibáért. A feladat megoldásának beküldési határideje március 15-re módosul.

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3522. Oldjuk meg az egész számok körében a

2x⁴+x²y²+5y²=y⁴+10x²

egyenletet. (3 pont)

B. 3523. Adott egy félkör. Tekintsük azokat a háromszögeket, amelyek egyik oldala tartalmazza a félkör átmérőjét, másik két oldala pedig érinti a félkört. E háromszögek közül melyiknek legkisebb a területe? (4 pont)

B. 3524. Az x, y valós számok összege 1. Határozzuk meg xy⁴+x⁴y legnagyobb értékét. (3 pont)

B. 3525. Bizonyítsuk be, hogy az 1,31,331,3331,... sorozatban végtelen sok összetett szám van. (4 pont)

B. 3526. Az ABCD téglalap BC oldalának felezőpontja F, CD oldalának a C-hez közelebbi harmadolópontja H. Milyen nagy lehet a HAF szög? (4 pont)

B. 3527. Adott egy trapéz, melynek a szárai nem párhuzamosak. Szerkesszünk csak vonalzóval olyan egyenest, amelynek a trapéz szárai közé eső szakaszát a trapéz átlói harmadolják. (5 pont)

B. 3528. Legyenek \(\displaystyle alpha\) és \(\displaystyle beta\) olyan hegyesszögek, amelyekre sin²\(\displaystyle alpha\)+sin²\(\displaystyle beta\)<1. Bizonyítsuk be, hogy sin²\(\displaystyle alpha\)+sin²\(\displaystyle beta\)<sin²(+). (4 pont)

B. 3529. Egy mértani sorozat első néhány tagjának összege 11, négyzetösszegük 341, köbösszegük 3641. Határozzuk meg a sorozat tagjait. (5 pont)

Javasolta: Besenyei Ádám, Budapest

B. 3530. Számítsuk ki \(\displaystyle {2002\choose0}-{2001\choose1}+{2000\choose2}-\dots-{1001\choose1001}\) értékét. (5 pont)

B. 3531. Az ABC háromszög O középpontú beírt körének az oldalakon levő érintési pontjai (a szokásos jelölésekkel) A₁, B₁, C₁. Az A₁O, B₁O, C₁O egyenesek rendre az A₂, B₂, C₂ pontokban metszik a B₁C₁, C₁A₁, A₁B₁ szakaszokat. Bizonyítsuk be, hogy az AA₂, BB₂ és CC₂ egyenesek egy ponton mennek át. (5 pont)

Javasolta: Besenyei Ádám, Budapest

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 284. Legyen f a véges S halmaz részhalmazain értelmezett függvény. Igazoljuk, hogy ha S tetszőleges A, B részhalmazaira

f(S\A)=f(A)   és   max(f(A),f(B))\(\displaystyle ge\)f(A\(\displaystyle cup\)B),

akkor f legfeljebb |S| különböző értéket vesz fel.

Schweitzer Miklós Emlékverseny, 2001

A. 285. Bizonyítsuk be, hogy ha az a>b>c>d>0 egész számokra

a²+ac-c²=b²+bd-d²,

akkor ab+cd összetett.

A. 286. Határozzuk meg mindazokat az f:RR folytonos függvényeket, amelyekre 1+xy\(\displaystyle ne\)0 esetén

\(\displaystyle f\left({x+y\over1+xy}\right)={f(x)f(y)\over|1+xy|}.\)

Győrfi Zoltán és Ligeti Gábor ötletéből

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. március 15.