 |
A 2002 márciusi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 287. Egy lapra valaki rajzolt egy ellipszist, amelynek a nagytengelye kétszer olyan hosszú, mint a kistengelye. Az illető a tengelyek végpontjait is megjelölte. Adjunk meg olyan szerkesztési eljárást, amely körzőt és vonalzót, valamint az ellipszist felhasználva, bármely hegyesszöget három egyenlő részre oszt.
Megoldás. Legyen 3\(\displaystyle alpha\) a harmadolandó szög, és vegyünk fel egy derékszögű koordináta-rendszert, amelyben az ellipszis egyenlete x2+4y2=1.
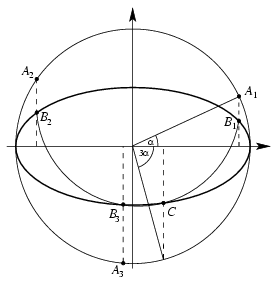
Legyen Ai=(cos( +(i-1).120o);sin(
+(i-1).120o);sin( +(i-1).120o)) és
+(i-1).120o)) és 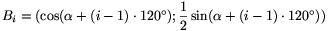 (i=1,2,3). Az Ai pontok az
egységkörön, a Bi pontok pedig az ellipszisen
vannak. A cél ezeknek a megszerkesztése.
(i=1,2,3). Az Ai pontok az
egységkörön, a Bi pontok pedig az ellipszisen
vannak. A cél ezeknek a megszerkesztése.
Tekintsük a Bi pontokon átmenő kört. Ez az
ellipszist egy negyedik C pontban is metszi. Némi számolással
ellenőrizhető, hogy a kör középpontja 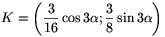 és
\(\displaystyle C=(\cos3\alpha;{1\over2}\sin3\alpha)\). A 3
és
\(\displaystyle C=(\cos3\alpha;{1\over2}\sin3\alpha)\). A 3 ismeretében a
kör megszerkeszthető és kimetszi az ellipszisből a
Bi pontokat.
ismeretében a
kör megszerkeszthető és kimetszi az ellipszisből a
Bi pontokat.
A. 288. Legyen p egy tetszőleges n-edfokú polinom, ahol n\(\displaystyle ge\)1. Bizonyítsuk be, hogy létezik legalább n+1 olyan komplex szám, amelyre p értéke 0 vagy 1.
IMC 7, London, 2000
Megoldás. Legyenek z1, ..., zk azok a komplex számok, ahol p értéke 0 vagy 1. Jelöljük \(\displaystyle mu\)j-vel, hogy zj hányszoros gyöke a p(z), illetve p(z)-1 polinomnak. Ekkor p'-nek a zj szám (\(\displaystyle mu\)j-1)-szeres gyöke. Multiplicitással számolva, a z1,...,zk számok között a p(z) és a p(z)-1 polinomoknak összesen 2n gyöke van, a p' polinomnak legfeljebb n-1, tehát
\(\displaystyle mu\)1+...+\(\displaystyle mu\)k=2n, (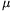 1-1)+...+(\(\displaystyle mu\)k-1)
1-1)+...+(\(\displaystyle mu\)k-1) n-1.
n-1.
Kivonva egymásból, k\(\displaystyle ge\)n+1.
A. 289. Bizonyítsuk be, hogy ha a pozitív valós számok halmazán értelmezett valós értékű f függvény minden pozitív x, y értékre eleget tesz az
\(\displaystyle f\left({x+y\over2}\right)+f\left({2xy\over x+y}\right)=f(x)+f(y)\)
egyenletnek, akkor minden pozitív x,y számpárra
\(\displaystyle 2f\big(\sqrt{xy}\big)=f(x)+f(y).\)
Schweitzer Miklós Emlékverseny, 2001
Megoldás. Legyenek a,b,c,d teszőleges pozitív valós számok. A függvényegyenletet többször alkalmazva,
f(a)+f(b)+f(c)+f(d)=
\(\displaystyle =f\left({a+b\over2}\right)+f\left({2ab\over a+b}\right)+f\left({c+d\over2}\right)+f\left({2cd\over c+d}\right)=\)
\(\displaystyle =f\left({{a+b\over2}+{c+d\over2}\over2}\right)+f\left({2{a+b\over2}\cdot{c+d\over2}\over{a+b\over2}+{c+d\over2}}\right)+\)
\(\displaystyle \qquad+f\left({{2ab\over a+b}+{2cd\over c+d}\over2}\right)+f\left({2{2ab\over a+b}\cdot{2cd\over c+d}\over{2ab\over a+b}+{2cd\over c+d}}\right)=\)
\(\displaystyle f\left({a+b+c+d\over4}\right)+f\left({(a+b)(c+d)\over a+b+c+d}\right)+\)
\(\displaystyle \qquad+f\left({abc+abd+acd+bcd\over(a+b)(c+d)}\right)+f\left({4abcd\over abc+abd+acd+bcd}\right).\)
Ha ugyanezt úgy is elvégezzük, hogy b-t és c-t felcseréljük, akkor azt kapjuk, hogy
| (1) | \(\displaystyle f\left({(a+b)(c+d)\over a+b+c+d}\right)+f\left({abc+abd+acd+bcd\over(a+b)(c+d)}\right)=\) |
\(\displaystyle \qquad=f\left({(a+c)(b+d)\over a+b+c+d}\right)+f\left({abc+abd+acd+bcd\over(a+c)(b+d)}\right).\)
Legyen a=c, b=a2/d és \(\displaystyle t={a\over b}+{b\over a}\). Mint könnyen ellenőrizhető,
\(\displaystyle {(a+b)(c+d)\over a+b+c+d}={abc+abd+acd+bcd\over(a+b)(c+d)}=a,\)
\(\displaystyle {(a+c)(b+d)\over a+b+c+d}=a\cdot{2t\over2+t},\)
végül
\(\displaystyle {abc+abd+acd+bcd\over(a+c)(b+d)}=a\cdot{2+t\over2t}.\)
Ezeket behelyettesítve (1)-be,
| (2) | \(\displaystyle 2f(a)=f\left(a\cdot{2t\over2+t}\right)+f\left(a\cdot{2+t\over2t}\right)\) |
A t bármilyen 2-nél nem kisebb szám lehet, a \(\displaystyle {2t\over2+t}\) pedig bármilyen 1-nél nem kisebb. Ezért minden x\(\displaystyle ge\)y számpárhoz léteznek olyan a és t számok, hogy \(\displaystyle a\cdot{2t\over2+t}=x\), \(\displaystyle a\cdot{2+t\over2t}=y\) és \(\displaystyle \sqrt{xy}=a\).

