A 2002. márciusi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 665. Mennyi az alábbi tört értéke, ha a számláló és a nevező ugyanannyi számjegyet tartalmaz?

$\displaystyle {166\dots6\over66\dots64}$

Megoldás. Jelölje n a számlálóban és a nevezőben található 6-os számjegyek közös számát. Ekkor

$\displaystyle \overline{166\ldots6}=10^n+6(1+10+\ldots+10^{n-1})=10^n+6\cdot\frac{10^n-1}{10-1}=$

$\displaystyle =10^n+\frac{2}{3}(10^n-1)=\frac{5}{3}10^n-\frac{2}{3}.$

Hasonlóan,

$\displaystyle \overline{66\ldots64}=60(1+10+\ldots+10^{n-1})+4=60\frac{10^n-1}{9}+4=$

$\displaystyle =\frac{20}{3}10^n-\frac{8}{3}=4\Bigg(\frac{5}{3}10^n-\frac{2}{3}\Bigg),$

tehát a tört értéke -- n értékétől függetlenül -- .

C. 666. Egy egész együtthatós másodfokú polinom minden egész helyen 3-mal osztható értéket vesz fel. Bizonyítsuk be, hogy a polinom mindhárom együtthatója osztható 3-mal.

Megoldás. Legyen a szóbanforgó polinom f=ax²+bx+c, ahol a, b és c egész számok. Ekkor a feltétel szerint 3|f(0)=c, így f-c=ax²+bx helyettesítési értékei is oszthatóak 3-mal. Ezért az 1 és a -1 helyeken fölvett helyettesítési értékei, a+b és a-b is oszthatók 3-mal. Tehát 3|(a+b)+(a-b)=2a és 3|(a+b)-(a-b)=2b, amiből a feladat állítása nyilvánvalóan következik.

C. 667. Legyen

$\displaystyle a=x+{1\over x},\qquad b=y+{1\over y},\qquad c=xy+{1\over xy}.$

Mutassuk meg, hogy az a²+b²+c²-abc kifejezés értéke nem függ x és y-tól.

Megoldás.

$\displaystyle a^2=\Big(x+\frac{1}{x}\Big)^2=x^2+\frac{1}{x^2}+2,$

$\displaystyle b^2=\Big(y+\frac{1}{y}\Big)^2=y^2+\frac{1}{y^2}+2,$

$\displaystyle c^2=\Big(xy+\frac{1}{xy}\Big)^2=x^2y^2+\frac{1}{x^2y^2}+2,$

valamint

$\displaystyle ab=\Big(x+\frac{1}{x}\Big)\Big(y+\frac{1}{y}\Big)=\Big(xy+\frac{1}{xy}\Big)+\Big(\frac{x}{y}+\frac{y}{x}\Big)=c+\Big(\frac{x}{y}+\frac{y}{x}\Big),$

így

$\displaystyle abc=c^2+\Big(\frac{x}{y}+\frac{y}{x}\Big)c=x^2y^2+\frac{1}{x^2y^2}+2+\Big(\frac{x}{y}+\frac{y}{x}\Big)\Big(xy+\frac{1}{xy}\Big)=$

$\displaystyle =x^2y^2+\frac{1}{x^2y^2}+2+\Big(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}\Big)=a^2+b^2+c^2-4,$

tehát a²+b²+c²-abc=4, valóban független az x és az y értékétől.

C. 668. Adott az ABC egyenlő oldalú háromszög. Hol vannak azok a P pontok a háromszög síkjában, amelyekre PA²=PB²+PC²?

Megoldás. Jelölje A^* az A pontnak a BC egyenesre vonatkozó tükörképét. Ha a háromszög oldalait egységnyi hosszúságúnak választjuk, akkor 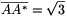; legyen 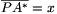. Írjuk fel a koszinusztételt rendre a PA^*A, PA^*B, PA^*C háromszögekre:

$\displaystyle \overline{PA}^2=\overline{PA^*}^2+\overline{AA^*}^2-2\overline{PA^*}\cdot\overline{AA^*}\cos PA^*A\angle=x^2+3-2x\sqrt{3}\cos PA^*A\angle,$

$\displaystyle \overline{PB}^2=\overline{PA^*}^2+\overline{A^*B}^2-2\overline{PA^*}\cdot\overline{A^*B}\cos PA^*B\angle=x^2+1-2x\cos PA^*B\angle,$

$\displaystyle \overline{PC}^2=\overline{PA^*}^2+\overline{A^*C}^2-2\overline{PA^*}\cdot\overline{A^*C}\cos PA^*C\angle=x^2+1-2x\cos PA^*C\angle.$

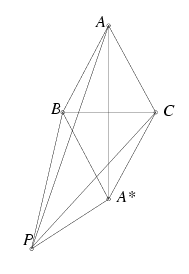
Vegyük észre, hogy a PA^*C és a PA^*B szögek különbsége BA^*C$\displaystyle angle$=60^o, e két szög számtani közepe pedig a PA^*A szög, hiszen AA^* felezi a BA^*C szöget. Vonjuk ki a második és harmadik egyenlőség összegéből az elsőt, és használjuk fel a

$\displaystyle \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}$

azonosságot:

$\displaystyle \overline{PB}^2+\overline{PC}^2-\overline{PA}^2=2x^2+2-(x^2+3)-2x(\cos PA^*B\angle+\cos PA^*C\angle-\sqrt{3}\cos PA^*A\angle)=$

$\displaystyle =x^2-1-2x(2\cos\frac{PA^*B\angle+PA^*C\angle}{2}\cos\frac{PA^*B\angle-PA^*C\angle}{2}-\sqrt{3}\cos PA^*A\angle)=$

$\displaystyle =x^2-1-2x(2\cos PA^*A\angle\cdot\cos30^{\circ}-\sqrt{3}\cos PA^*A\angle)=$

$\displaystyle =x^2-1-2x\cos PA^*A\angle\cdot(2\frac{\sqrt{3}}{2}-\sqrt{3})=x^2-1.$

Tehát a feltételnek azok a P pontok felelnek meg, amelyekre $\displaystyle \overline{PA^*}=x=1$, vagyis amelyek illeszkednek az A^* középpontú, egységsugarú körre.

C. 669. Adott kerületű körcikkek közül melyiknek legnagyobb a területe?

Megoldás. A vizsgált körcikkek sugarát jelöljük r-rel, szögüket pedig -- ívmértékben számolva -- -val; az adott kerület legyen K. Ekkor K=2r+r=r(2+$\displaystyle alpha$), a körcikk területének kétszerese pedig 2t=r²$\displaystyle alpha$. Így

$\displaystyle 2t=r^2\Big(\frac{K}{r}-2\Big),$ ezért .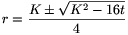

Mivel a diszkrimináns nem lehet negatív, azért t legfeljebb $\displaystyle \frac{K^2}{16}$ lehet, és ezt az értéket akkor veszi fel, ha $\displaystyle r=\frac{K}{4}$. Ekkor pedig $\displaystyle K=r(2+\alpha)=\frac{K}{4}(2+\alpha)$, ahonnan $\displaystyle alpha$=2, ami $\displaystyle 360\cdot\frac{2}{2\pi}\approx114,59^{\circ}$.