A 2002. májusi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 675. Van-e olyan négyzetszám, amelynek utolsó két számjegye páratlan?

Megoldás. A keresett szám csak egy páratlan számnak lehet a négyzete, ezért (2k+1)²=4k(k+1)+1

alakú; így 4-gyel (sőt, 8-cal is) osztva 1-et ad maradékul. Páratlan négyzetszám utolsó jegye 1, 5 vagy 9 lehet, esetünkben ez azt jelenti, hogy a szám 20-szal való osztási maradéka 11, 15 vagy 19. Az ezeknek megfelelő 4-gyel való osztási maradék azonban mindig 3, ami előbbi megállapításunknak ellentmond. Tehát egy négyzetszámnak nem lehet az utolsó két számjegye egyszerre páratlan.

C. 676. Az ABEF téglalap AB oldala 1, BE oldala 3 egység. A BE oldal harmadolópontjai C és D. Mutassuk meg, hogy

BAC\(\displaystyle \angle\)+BAD+BAE\(\displaystyle \angle\)=180^o.

Megoldás.

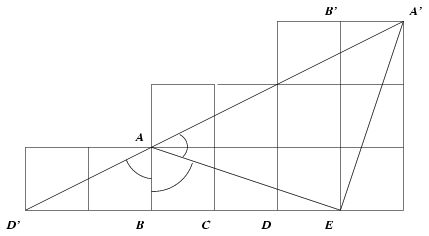
Az ábráról leolvasható, hogy BAD'\(\displaystyle angle\)=BAD\(\displaystyle angle\) és BAC\(\displaystyle angle\)=45^o=EAA'\(\displaystyle angle\), tehát BAD\(\displaystyle angle\)+BAE\(\displaystyle angle\)+BAC\(\displaystyle angle\)=D'AB\(\displaystyle angle\)+BAE\(\displaystyle angle\)+EAA'=180^o. (A feladat a tangensfüggvény addíciós képletének felhasználásával is megoldható.)

C. 677. Határozzuk meg az a és b egész számokat, ha a⁴+(a+b)⁴ +b⁴ négyzetszám.

Megoldás. Négyzetszám 4-gyel (maradékosan) osztva 0-t vagy 1-et adhat maradékul, előbbit akkor, ha páros, utóbbit akkor, ha páratlan. Így az a, b, a+b közül legfeljebb egy lehet páratlan, akkor viszont a és b egyaránt páros: a=2a₁, b=2b₁. Ezért, ha a⁴+(a+b)⁴+b⁴=16(a₁⁴+(a₁+b₁)⁴+b₁⁴) négyzetszám, akkor a₁⁴+(a₁+b₁)⁴+b₁⁴ is az. Így a₁ és b₁ egyaránt páros, és így tovább. Azt kaptuk, hogy a és b a 2-nek akárhányadik hatványával osztható, ami csak akkor lehetséges, ha a=b=0; ez másrészt ki is elégíti a feladat feltételét.

C. 678. Az ABC háromszögben AC=1, ABC\(\displaystyle \angle\)=30^o, BAC=60^o, a C-ből induló magasság talppontja D. Milyen messze van egymástól az ACD és a BCD háromszögek beírt körének a középpontja?

Megoldás.

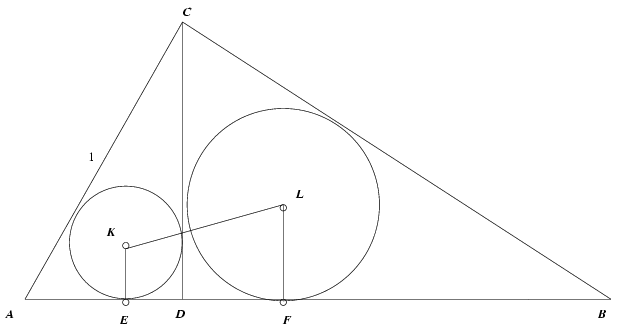
Az ABC (nevezetes) derékszögű háromszög, 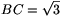, AB=2^.AC=2. Az ACD háromszög kerülete: \(\displaystyle k_{ACD}={1\over2}k_{ABC}={{3+\sqrt{3}}\over2}\), hasonlóan 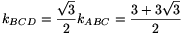. A megfelelő területek: \(\displaystyle t_{ACD}={1\over4}t_{ABC}={1\over4}\cdot{{\sqrt{3}}\over2}={{\sqrt{3}}\over8}\), \(\displaystyle t_{BCD}={3\over4}t_{ABC}={3\over4}\cdot{{\sqrt{3}}\over2}={{3\sqrt{3}}\over8}\). 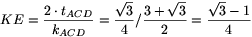Így a kis háromszögekbe írható körök sugara: , \(\displaystyle LF={{2\cdot t_{BCD}}\over{k_{BCD}}}={{3\sqrt{3}}\over4}/{{3+3\sqrt{3}}\over2}={{3-\sqrt{3}}\over4}\). Végül \(\displaystyle ED={{k_{ACD}}\over2}-AC={{3+\sqrt{3}}\over4}-1={{\sqrt{3}-1}\over4}\), \(\displaystyle DF={{k_{BCD}}\over2}-BC={{3+3\sqrt{3}}\over4}-\sqrt{3}={{3-\sqrt{3}}\over4}\), ezért Pitagorasz tételéből \(\displaystyle KL=\sqrt{EF^2+(LF-KE)^2}=\sqrt{\frac{1}{4}+\frac{(2-\sqrt{3})^2}{4}}=\sqrt{2-\sqrt{3}}\approx0.52\).

C. 679. Adott három egységsugarú gömb, melyek páronként érintik egymást és az S síkot. Határozzuk meg annak a gömbnek a sugarát, melynek középpontja az S síkon van és érinti a gömböket.

Megoldás.

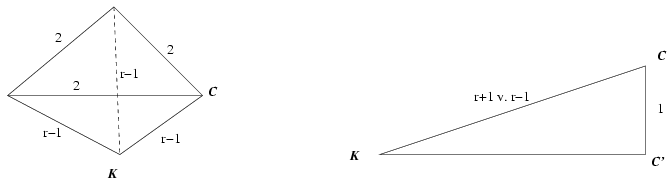
A három egységsugarú gömb középpontja egy 2 oldalhosszúságú, az S síkkal párhuzamos, attól 1 távolságra levő szabályos háromszöget határoz meg. A keresett r sugarú gömb K középpontja a háromszög mindhárom csúcsától r\(\displaystyle pm\)1 távolságra van aszerint, hogy az egységgömböket kívülről vagy belülről érinti. Jelölje a három középpont egyikét C, ennek az S síkra való merőleges vetülete legyen C'. A KC'C derékszögű háromszögben Pitagorasz tétele miatt \(\displaystyle KC'=\sqrt{KC^2-C'C^2}=\sqrt{(r\pm1)^2-1}=\sqrt{r^2\pm2r}\). Másrészt KC' hossza egyenlő a 2 egységnyi élű szabályos háromszög középpontjának a csúcsoktól való távolságával, \(\displaystyle {2\over{\sqrt{3}}}\)-mal. Így \(\displaystyle r^2\pm2r={4\over3}\), tehát \(\displaystyle r={{\sqrt{21}\pm3}\over3}\). Mindvégig feltételeztük, hogy a keresett sugarú gömb vagy mindhárom egységgömböt kívülről, vagy mindegyiket belülről érinti. ,,Vegyes'' konfiguráció nem létezik, mivel ha a K középpontú, r sugarú gömb a G₁ középpontú gömböt kívülről, a G₂ középpontút pedig belülről érintené, akkor KG₁=r+1, KG₂=r-1 szerint G₁G₂=2=(r+1)-(r-1)=KG₁-KG₂, azaz a G₁G₂K háromszög elfajuló, tehát K a G₁G₂ egyenesen lenne. Ez az egyenes azonban párhuzamos az S síkkal, ezért nincs vele közös pontja.