 |
A 2002 szeptemberi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 296. András gondolt egy 16-nál nem nagyobb pozitív egészre. Béla feltehet 7 eldöntendő kérdést, amelyre András igennel vagy nemmel válaszolhat, és egyszer rossz választ is adhat. Segítsünk Bélának kitalálni a gondolt számot.
Cseh versenyfeladat
Megoldás. Kódoljuk a 16 lehetséges gondolt számot 4 jegyből álló 0-1 sorozatokkal; a gondolt számnak megfelelő négy jegy legyen x1, x2, x3 és x4. Béla hét kérdésében azt kérdezze meg, hogy az x1, x2, x3, x4, x1+x2+x3, x1+x2+x4, x1+x3+x4 kifejezések páratlanok-e. A kapott válaszokat szintén 0-val és 1-gyel kódolva, jelöljük a válaszokat V1, V2, V3, V4, V1,2,3, V1,2,4 és V1,3,4. (Tehát, például V1,2,3 akkor 1, ha x1+x2+x3 páratlan.)
Ha V1+V2+V3+V1,2,3 páros, akkor ezek a válaszok pontosak. Ebben az esetben x1-et, x2-t és x3-at ismerjük. Az x4-re a többi három válasz mindegyikéből következtethetünk. Mivel egy válasz hibás is lehet, az x4-nek az a helyes értéke, amelyiket legalább kétféleképpen megkapunk.
Hasonlóan járunk el, ha V1+V2+V4+V1,2,4, illetve ha V1+V3+V4+V1,3,4 páros.
Ha V1+V2+V3+V1,2,3, V1+V2+V4+V1,2,4, V1+V3+V4+V1,3,4 mindegyike páratlan, akkor mindegyik négyesben hibás az egyik válasz. Az egyetlen közös elem a V1. A többi válasz tehát pontos, ezekből x1, x2, x3, x4 mindegyike meghatározható.
Megjegyzés. A feladat az algebrai kódelmélethez, ezen belül is a Hamming-kódok konstrukciójához kapcsolódik. Legyen k pozitív egész, h=2k-1 és m=h-k. Az ,,(m,h) Hamming-kód'' h hosszúságú 0-1 sorozatok egy halmaza, a halmaz elemeinek száma 2m, és tetszőleges h hosszúságú 0-1 sorozathoz pontosan egy olyan kódbeli sorozat létezik, hogy a két sorozat legfeljebb egy helyen különbözik.
Például, a ,,(4,7) Hamming-kód'' a következő sorozatokból áll:
| 0000000 | 0100101 | 1000011 | 1100110 |
| 0001111 | 0101010 | 1001100 | 1101001 |
| 0010110 | 0110011 | 1010101 | 1110000 |
| 0011001 | 0111100 | 1011010 | 1111111 |
A feladat nem más, mint a (4,7) Hamming-kóddal egyenértékű konstrukció keresése.
A kódelmélet iránt érdeklődő Olvasóinknak Pelikán József Algebrai Kódelmélet c. cikkét (KöMaL 1993/5, 193-199. oldal) ajánljuk.
A. 297. Legyenek a0,a1,a2,... pozitív egészek úgy, hogy a0=1, a1>1 és
\(\displaystyle a_{n+1}=\frac{a_1\cdot\ldots\cdot a_n}{a_{[n/2]}}+1\)
teljesül minden n=1,2,... esetén. ([x] jelöli az x egész részét.) Mutassuk meg, hogy a
\(\displaystyle \sum_{n=1}^\infty\frac{1}{a_{n+1}a_{[n/2]}}\)
sor összege egy racionális szám.
Cseh versenyfeladat
Megoldás. Tetszüleges N pozitív egészre
\(\displaystyle \sum_{n=1}^N{1\over a_{n+1}a_{[n/2]}} =\sum_{n=1}^N{1\over a_{n+1}\displaystyle{a_1\cdot\dots\cdot a_n\over a_{n+1}-1}} =\sum_{n=1}^N{a_{n+1}-1\over a_1\cdot\dots\cdot a_{n+1}}=\)
\(\displaystyle =\sum_{n=1}^N\left({1\over a_1\cdot\dots\cdot a_n}-{1\over a_1\cdot\dots\cdot a_{n+1}}\right)={1\over a_1}-{1\over a_1a_2\dots a_{N+1}}.\)
Mivel a2,a3,... mindegyike nagyobb 1-nél, \(\displaystyle {1\over a_1a_2\dots a_{N+1}}\le{1\over2^N}\), és így
\(\displaystyle \sum_{n=1}^\infty{1\over a_{n+1}a_{[n/2]}}={1\over a_1}.\)
A. 298. Egy gömbháromszög szögei 
, 
, 
, a velük
szemközti oldalívek hossza a, b, illetve
c. Igazoljuk, hogy
a.cos\(\displaystyle beta\)+b.cos<c.
Megoldás. Legyen O a gömb középpontja, amelyen a háromszög elhelyezkedik; a csúcsokat a szokásos módon jelöljük A, B, C-vel. Feltételezhetjük, hogy a gömb sugara egységnyi. Tekintsük az OAB, OBC és OCA körcikkeket; ezek területe c/2, a/2, illetve b/2.
Vetítsük most a három körcikket az OAB síkra és jelöljük C'-vel a C pont vetületét, továbbá legyen A' és B' az A-val, illetve B-vel átellenes pont. A vetítés miatt C' az O középpontú egységkör belsejébe esik. Az AC és BC ívek vetülete egy AA', illetve egy BB' nagytengelyű ellipszis megfelelő íve. A két ellipszis összesen 4 pontban metszi egymást: mindkét, az A és A' pontokat összekötő félellipszis metszi mindkét, a B és B' pontokat összekötő félellipszist. Több metszéspont nem lehet, mert két különböző kúpszelet legfeljebb 4 pontban metszheti egymást.
Az OBC és OCA körcikkek vetületének
előjeles területe (a/2).cos , illetve
(b/2).cos \(\displaystyle \alpha\). A feladat állítása tehát ekvivalens
azzal, hogy e két eljőjeles terület összege kisebb, mint az OAB
körcikk területe.
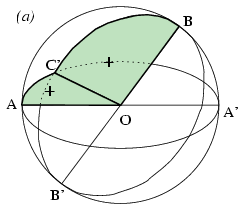
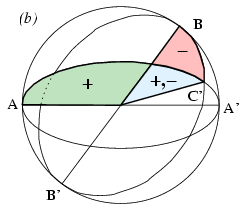
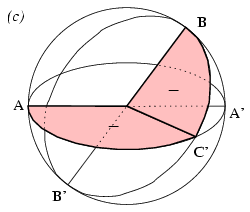
Összesen három lényegesen különböző esetet különböztethetünk meg aszerint, hogy C' az AA' és BB' egyenesek melyik oldalára esik; ezeket láthatjuk az ábrán. (A teljes megoldáshoz az olyan elfajuló eseteket is meg kell vizsgálni, amikor C' pontosan az AA' vagy a BB' egyenesre esik; ezeket két esethez is sorolhatjuk.) Az ábrán zöld színnel jelöltük azokat a területeket, amik a két vetített körcikk előjeles területében pozitív előjellel szerepelnek, piros színnel azokat, ahol negatív előjellel szerepelnek. A (b) esetben van egy olyan terület, ami mindkét vetületben szerepel, mégpedig ellentétes előjellel; ezt kék színnel jelöltük.
Mindhárom esetben igaz, hogy a zölddel jelölt vetületdarabok nem nyúlnak egymásba, részei az OAB körcikknek, de azt nem fedik le teljesen. Ezért a két előjeles terület összege mindig kisebb, mint az OAB körcikk területe.