 |
A 2002 októberi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 299. Az ABCD négyzet belsejében P és Q olyan pontok, amelyekre
PAQ\(\displaystyle \angle\)=PCQ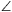 =45o.
=45o.
Fejezzük ki a PQ szakasz hosszát a BP és DQ szakaszok hosszával!
A tanárképző főiskolások Péter Rózsa matematikaversenye, 2002
Megoldás. Legyen BP=p, DQ=q és PQ=x. A p és q hosszúságokkal kell kifejeznünk x-et.
A P és Q pontok közül az egyik az ABC, a másik az ACD háromszög belsejébe esik. Ennek megfelelően két esetet kell megkülönböztetnünk.
1. Ha a a P pont az ABC háromszög, a Q pont pedig az ACD háromszög belsejébe esik, akkor az APQ és a CQP háromszög is az ABCD négyzettel azonos körüljárású.
Tükrözzük a B pontot az AP és a CP egyenesekre; a két tükörkép legyen U, illetve V. A tükrözés miatt AU=AB=AD, és az A csúcsnál fekvő szögek összeszámolásából kapjuk, hogy QAU\(\displaystyle \angle\)=DAQ\(\displaystyle \angle\). Ebből következik, hogy az AQU és AQD háromszögek egybevágók. Hasonlóan kapjuk, hogy a CQV és CQD háromszögek is egybevágók.
Az egybevágóságok miatt az ábrán egyforma színnel jelölt szögek egyenlők, PU=PV=PB=p és QU=QV=QD=q. A PQU és PQV háromszögek egybevágók, mert oldalaik ugyanakkorák. Ezért az U-nál és V-nél fekvő szögeik egyenlőek. Ennek a két szögnek az összege megegyezik az ABCD négyzet B-nél és D-nél levő szögeinek összegével, tehát PUQ\(\displaystyle \angle\)=PVQ\(\displaystyle \angle\)=90o. A Pitagorasz-tételből tehát
\(\displaystyle x=\sqrt{p^2+q^2}.\)
A gondolatmenetből az is következik, hogy a kékkel és a sárgával jelölt szögek, illetve a pirossal és a zölddel jelölt szögek egyenlőek, és a BP szakasz párhuzamos a QD szakasszal.
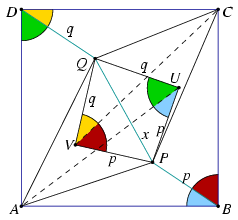
2. Ha a Q pont az ABC háromszög, a P pont pedig az ACD háromszög belsejébe esik, akkor az APQ háromszög és a CQP háromszög is az ABCD négyzettel ellentétes körüljárású. Ebben az esetben a megoldás (és a végeredmény is) lényegesen bonyolultabb.
Mint láttuk, a QBPD négyszög trapéz, alapjai QB és PD, továbbá PQ2=BQ2+DP2. A pontok elhelyezkedéséből azt is megállapíthatjuk, hogy BP>DP és BQ<DQ.
Először megmutatjuk, hogy minden ilyen tulajdonságú trapézhoz találhatók olyan A és C pontok, amelyekre ABCD négyzet és PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o.
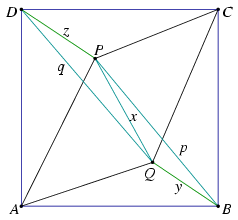
Legyen tehát QBPD egy olyan trapéz, amelyben PQ2=BQ2+DP2. Legyen U és V az a két pont, amelyre QU=QV=BQ és PU=PV=DP; az U pont a PQ átlónak a B-vel megegyező oldalán legyen, a V pont pedig a D csúccsal megegyező oldalon. A Pitagorasz-tétel megfordítása szerint PUQ\(\displaystyle \angle\)=PVQ\(\displaystyle \angle\)=90o.
Legyen A a BQU szög és a DPU szög felezőjének metszéspontja, C pedig legyen a BQV szög felezőjének és a DPV szög felezőjének metszéspontja.
Az AB, AU és AD szakaszok egyenlő hosszúságúak, mert szimmetrikusak az AQ, illetve AP egyenesekre. Hasonlóképpen CB=CV=CD, mert ez a három szakasz is szimmetrikus a CQ, illetve CP egyenesekre. Az ABQUPD és CDPVQB hatszögek szögeinek összeszámolásából kapjuk, hogy PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o és PAD\(\displaystyle \angle\)=BCD\(\displaystyle \angle\)=90o. Mindezekből az is következik, hogy az ABCD négyszög egy négyzet.
Az BP>DP és BQ<DQ feltételek biztosítják, hogy az U és a V pont a PQB, illetve a QPD szögtartomány belsejébe esik, az A és B, illetve C és D pontok a PQ egyenes ellentétes oldalain vannak, és az ABCD négyzet valóban a belsejében tartalmazza a PQ szakaszt.
Jelöljük a négyzet oldalának hosszát a-val, továbbá legyen BQ=y és QD=z. Az a, p, q szakaszok hosszával fogjuk kifejezni x-et. A pontok elhelyezkedéséből látható, hogy \(\displaystyle {1\over\sqrt2}a Mint már láttuk, x2=y2+z2. A BD szakasz a négyzet átlója, ezért \(\displaystyle BD=\sqrt2a\). Tekintsük a QBPD trapézt. Legyen QBP\(\displaystyle \angle\)=\(\displaystyle \beta\) és PDQ\(\displaystyle \angle\)=\(\displaystyle \delta\). Írjuk fel a koszinusz-tételt a QBP, BPD, PDQ és DQB háromszögekre: x2=p2+y2-2pycos \(\displaystyle \beta\) 2a2=p2+z2+2pzcos \(\displaystyle \beta\) x2=q2+z2-2qzcos \(\displaystyle \delta\) 2a2=q2+y2+2qycos \(\displaystyle \delta\) A koszinuszokat eliminálva, Az (1) és (2) egyenletek összegét (y+z)-vel osztva: x2+2a2=p2+q2+2yz, amiből (y-z)2=x2-2yz=p2+q2-2a2 és (y+z)2=x2+2yz=2x2+2a2-p2-q2. Az (1) és (2) egyenletek különbségét négyzetre emelve, (2a2-x2)2(y-z)2=(p2-q2)2(y+z)2 (2a2-x2)2(p2+q2-2a2)=(p2-q2)2(2x2+2a2-p2-q2) A 2a2-x2 számot ebből a (legfeljebb) másodfokú egyenletből fogjuk kiszámítani. A fő együttható nemnegatív: p2+q2-2a2=(y-z)2\(\displaystyle \ge\)0. Ha a fő együttható 0, azaz p2+q2-2a2=(y-z)2=0, akkor y=z, a QBPD négyszög paralelogramma és p=q=a. Könnyű végiggondolni, hogy ha P és Q a B, illetve D középpontú, a sugarú körön, a négyzet középpontjára szimmetrikusan helyezkedik el, akkor a PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o biztosan teljesül. A PQ szakasz hosszáról ilyenkor nem mondhatunk többet, mint hogy a \(\displaystyle [(2-\sqrt2)a,\sqrt2a)\) intervallumba esik. Ha a fő együttható pozitív, akkor a (3) egyenletre alkalmazhatjuk a másodfokú egyenlet megoldóképletét. Mivel a konstans tag negatív, az egyenletnek egy pozitív és egy negatív valós gyöke van. Azt is tudjuk, hogy \(\displaystyle x<\sqrt2a\), azaz 2a2-x2>0, tehát a pozitív gyökre van szükségünk: \(\displaystyle 2a^2-x^2={-(p^2-q^2)^2+\sqrt{(p^2-q^2)^4+
(p^2+q^2-2a^2)(p^2-q^2)^2(6a^2-p^2-q^2)}\over p^2+q^2-2a^2}=\) \(\displaystyle ={-(p^2-q^2)^2+2|p^2-q^2|\sqrt{-3a^4+2a^2(p^2+q^2)-p^2q^2}
\over p^2+q^2-2a^2},\) \(\displaystyle x=\sqrt{2a^2+{(p^2-q^2)^2-2|p^2-q^2|\sqrt{-3a^4+2a^2(p^2+q^2)-p^2q^2}
\over p^2+q^2-2a^2}}.\)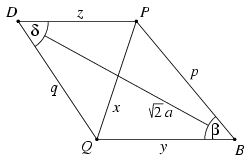
(1) x2z+2a2y=(p2+yz)(y+z),
(2) x2y+2a2z=(q2+yz)(y+z).
(3) (p2+q2-2a2)(2a2-x2)2+2(p2-q2)2(2a2-x2)-(p2-q2)2(6a2-p2-q2)=0. 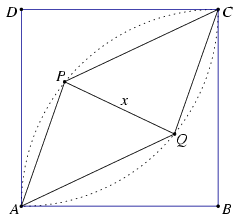
A. 300. Adjuk meg mindazokat az egészekből álló (a,b) számpárokat, amelyekre a2+ab+b2 osztható 75-nel.
Megoldás. Tekintsük a következő azonosságokat.
| (2.1) | (x-2y)(2x-y)=2(x2+xy+y2)-7.xy; |
| (2.2) | (x-18y)(18x-y)=18(x2+xy+y2)-73.xy; |
| (2.3) | (x-1353y)(1353x-y)=1353(x2+xy+y2)-109.75.xy. |
Ezekből leolvasható, hogy a2+ab+b2 akkor osztható 75-nel, ha a következő feltételek valamelyike teljesül:
- a és b is osztható 73-nel;
- a=72p, b=72q, ahol p\(\displaystyle \equiv\)2q (mod 7) vagy q\(\displaystyle \equiv\)2p (mod 7);
- a=7p, b=7q, ahol p\(\displaystyle \equiv\)18q (mod 73) vagy q\(\displaystyle \equiv\)18p (mod 73);
- a\(\displaystyle \equiv\)1353b (mod 75) vagy b\(\displaystyle \equiv\)1353a (mod 75).
A. 301. Legyen
a0,a1,... nemnegatív számokból
álló sorozat, amelyre tetszőleges k,m 0 esetén
0 esetén
ak+m ak+m+1+akam.
ak+m+1+akam.
Tegyük fel, hogy elég nagy n esetén nan<0,2499. Bizonyítsuk be, hogy létezik olyan 0<q<1 szám, amelyre elég nagy n esetén
an<qn.
Lengyel versenyfeladat
Megoldás. Legyen p=0,2499 és legyen \(\displaystyle 1 Tetszőleges N\(\displaystyle \ge\)n0 esetén legyen \(\displaystyle S(N)=\sup\{na_n:~n\ge k\}\). Az n0 választása szerint például S(n0)\(\displaystyle \le\)p. Ha N\(\displaystyle \ge\)n0 és n\(\displaystyle \ge\)2N, akkor \(\displaystyle na_n=n\sum_{k=n}^\infty(a_k-a_{k+1})\le n\sum_{k=n}^\infty a_{[k/2]}a_{[(k+1)/2]}\le n\sum_{k=n}^\infty{S(N)\over\big[{k\over2}\big]}
\cdot{S(N)\over\big[{k+1\over2}\big]}<\) \(\displaystyle Ez minden n\(\displaystyle \ge\)2N-re igaz, ezért \(\displaystyle S(2N)=\sup\{na_n:~n\ge2N\}\le4rS^2(N),\) vagy másképpen 4rS(2N)\(\displaystyle \le\)(4rS(N))2. Ezt többször alkalmazva kapjuk, hogy \(\displaystyle S(2^mN)\le{1\over4r}\big(4rS(N)\big)^{2^m}<
\big(4rS(N)\big)^{2^m}.\) Legyen most n>n0 tetszőleges pozitív egész. Válasszuk meg az m nemnegatív egészt úgy, hogy 2mn0\(\displaystyle \le\)n<2m+1n0 teljesüljön. Ekkor \(\displaystyle a_n\le{1\over n}S(2^mn_0)<
{1\over n}\big(4rS(n_0)\big)^{2^m}<
\big(4pr\big)^{2^m}<
\big(4pr\big)^{n/2n_0}
\le\left(\root{2n_0}\of{4pr}\right)^n.\) Az r számot úgy választottuk, hogy 4pr<1 teljesüljön, így a \(\displaystyle q=\root{2n_0}\of{4pr}\) szám megfelel a feladat feltételeinek.

