Fizikából kitűzött gyakorlatok és feladatok
2002. november

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 237. Készítsünk 1,5 méter hosszú fonálingát, amelynek nehezéke egy pingponglabda! Hogyan függ a légellenállási erő munkája (vagyis az energiaveszteség) az indítás h magasságától? Mekkora a légellenállási erő átlagos teljesítménye egy fél lengés során? (6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3561. Az egyik balesetvédelmi reklám szerint ha 50 km/h sebességgel egy falnak ütközünk, annak ugyanaz a következménye, mintha a 4. emeletről estünk volna le. Vajon mekkora átlagos emeletmagasságra gondoltak? (3 pont)

Közli: Kopcsa József, Debrecen

(Mikola-verseny feladat)

P. 3562. Egy kertészetben gyümölcsös ládák szállítására földre fektetett acéllapot használnak, amelyet traktorral húznak. A lap tömege 20 kg, a lapon 400 kg gyümölcs van. A lap és a talaj közötti súrlódási együttható 0,6. Mennyire melegszik fel a lap 100 méteres úton, ha a súrlódási munka 40%-a az acéllap belső energiáját növeli? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

P. 3563. Két autó halad egyenes, keskeny úton egymás után. Mindkét jármű sebessége 72 km/h. Az elöl haladó autó fékezni kezd és egyenletesen lassulva megáll, miközben sebessége másodpercenként 5 m/s-mal csökken. A másik autó vezetőjének reakcióideje 1 másodperc, és sebességét másodpercenként 4 m/s-mal tudja csökkenteni.

a) Legalább mekkora legyen a követési távolság, hogy a járművek ne ütközzenek össze?

b) A minimális követési távolság betartása mellett az elöl haladó jármű fékezésének megkezdése után mennyi idő múlva lesznek a járművek 22 m távolságra egymástól? (4 pont)

Közli: Szegedi Ervin, Debrecen

(Mikola-verseny feladat)

P. 3564. Hány darab 25 cm átmérőjű léggömböt lehet megtölteni a 0,1 m³ térfogatú, 1,5^.10⁷ Pa nyomású héliumgázzal töltött gázpalackból? A léggömbökben a nyomás 1,02^.10⁵ Pa-ra emelkedik, amikor a betöltött gáz hőmérséklete kiegyenlítődik a környezetével. A palackot napokkal előbb a töltőhelyre szállították. (4 pont)

Közli: Hilbert Margit, Szeged

(Tornyai-verseny feladat)

P. 3565. Legalább mekkora térfogatú legyen az az edény, amelyben 15 liter 80 ^oC hőmérsékletű vizet úgy akarunk 25 ^oC-ra lehűteni, hogy 0 ^oC hőmérsékletű jeget teszünk bele, és nem akarjuk, hogy kifolyjon az edényből a víz? (3 pont)

Közli: Holics László, Budapest

P. 3566. Egy 1,5 méter magas faltól 2 méterre, a talaj szintjéről indítva át akarunk dobni a fal felett egy 5 kg tömegű súlygolyót.

a) Milyen irányú legyen a 8 m/s nagyságú kezdősebesség, hogy a súlygolyó a fal mögött a lehető legmesszebb essen le? Mekkora ez a távolság?

b) Mekkora legkisebb energiabefektetéssel hajítható át az adott helyről a súlygolyó? Milyen irányú ebben az esetben a kezdősebesség? (5 pont)

Közli: Szűcs József, Pécs

(Párkányi-verseny feladat)

P. 3567. Határozzuk meg az ábrán látható két besatírozott terület nagyságát integrálszámítás alkalmazása nélkül, valamilyen egyszerű fizikai gondolatmenettel!

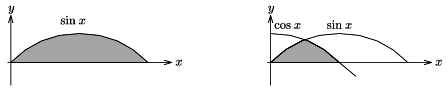
(5 pont)

Közli: Sári Péter, Budapest

P. 3568. Vízszintes fém mennyezetre m tömegű pontszerű nehezékkel ellátott fonálingát kötünk. Az inga lengésideje kis kitérések esetén T₁. Ezután a nehezékre elektromos töltést viszünk, majd ismét kis kitérésű lengésbe hozzuk. A fonál szigetelő. Lengésidejét most T₂-nek mérjük.

Mekkora töltést vittünk a nehezékre?

(Adatok: m= 5 g, T₁=2,02 s, T₂=2,03 s, g=9,81 m/s².) (5 pont)

Közli: Légrádi Imre, Sopron

P. 3569. Hidrogéngázzal töltött kisülési csövön működés közben 1,12 A áram folyik. Hány elektron halad át a cső keresztmetszetén másodpercenként, ha a negatív elektródából kilépő elektronok száma másodpercenként 3^.10¹⁸? (4 pont)

Közli: Radnai Gyula, Budapest

P. 3570. U feszültségű szinuszos generátorra sorosan R ellenállást, L induktivitást és C kapacitást kapcsoltunk. Az induktivitás változtatható, növelése közben először az áram is nő, majd csökkenni kezd. Az áramerősség legnagyobb értéke I₀, ekkor a tekercs feszültsége U₀.

Az induktivitást tovább növelve a tekercs feszültsége tovább nő, elér egy maximális U_max  értéket, majd csökkenni kezd.

Határozzuk meg az U_max /U₀ arányt, és számítsuk ki értékét \(\displaystyle R=2\sqrt{2}X_C\) esetén! (5 pont)

Közli: Veres Zoltán, Margitta (Románia)

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. december 11.