A számítástechnika-versenyben kitűzött feladatok 2002. november

Kérjük, olvassa el a versenykiírást.

I. 34. A binomiális együtthatók felhasználhatók számok speciális számrendszerben, az ún. binomiális számrendszerben való felírására. Rögzített m (2m 50) esetén minden nemnegatív n (0 $\displaystyle \le$n $\displaystyle \le$10 000) szám egyértelműen felírható az alábbi formában: 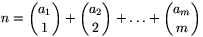, ahol 0 $\displaystyle \le$a₁ < a₂ < ...< a_m.

Készítsünk programot (I34.pas, ...), amely beolvassa n és m értékét, majd kiírja a hozzá tartozó a₁,a₂,..., a_m értékét!

Pl.: n=41 esetén a₁ = 1, a₂ = 2, a₃ = 4, a₄ = 7, azaz

$\displaystyle 41={1\choose1}+{2\choose2}+{4\choose3}+{7\choose4}=1+1+4+35.$ (10 pont)

I. 35. Egy R sugarú, H magasságú henger palástja alján elhelyezünk egy hangyát. A hangya percenként M centimétert mászik felfelé. A hengert tengelye (ami a koordinátarendszer Z tengelye) körül megforgatjuk az óramutató járásával ellentétes irányban, egy fordulatot T perc alatt tesz meg. A hangya az (R,0,0) pontból indul, és pályáját az Y=0 síkra vetítjük. A vetítősugarak az Y-tengellyel ALFA fok szöget zárnak be (1. ábra).

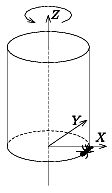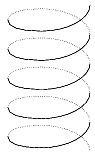1. ábra	2. ábra

Készítsünk programot (I35.pas, ...), amely beolvassa R (1 $\displaystyle \le$R$\displaystyle \le$50), H (1 $\displaystyle \le$H 200), M (1 M H), T (1T 100) és ALFA (0 ALFA<90) értékét, majd az Y=0 síkra vetített ábrát rajzol a hangya pályájáról a henger látható oldalán folytonos, hátoldalán pedig pontozott vonallal.

R=50, H=200, M=1, T=40, ALFA=30 esetén a 2. ábrán látható rajzot kapjuk. (10 pont)

I. 36. A trinomiális tétel szerint:

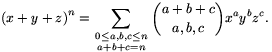
A képletben használt zárójeles formula az ún. trinomiális együtthatókat tartalmazza, melyeket az alábbi képlettel is számolhatunk:

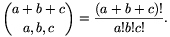
Az ebben a képletben szereplő faktoriális értékek azonban túlságosan nagyok, így kiszámításuk nem mindig végezhető el. A trinomiális együtthatók kiszámítása azonban visszavezethető binomiális együtthatók szorzatára is, ami ezt a problémát megoldja.

Készítsünk táblázatot (I36.xls), amelynek egy adott mezőjébe beírva n (n= a+b+c, n 20) értékét, az alábbi jellegű táblázatot kapjuk a trinomiális együtthatókról!

Példa: n=5 esetén a táblázat:

(10 pont)

A számítástechnike feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2002. december 13.