 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
I. 37. Készítsünk programot (I37.pas, ...),
amely egy A (2\(\displaystyle \le\)A \(\displaystyle \le\)100) alapú számrendszerben felírt fixpontos valós számot
(legfeljebb 100 jegy van a tizedespontja előtt, valamint a
tizedespontja mögött is) átalakít B alapú (2
B 100) számrendszerben
felírt számmá. (10 pont)
I. 38. Egy szakaszból (x1,y1,x2,y2) sokféle síkbeli alakzatot készíthetünk transzformációk sorozatával. A legegyszerűbb esetben a szakaszt eltoljuk (paramétere a dx és a dy valós számok), s eltolás közben a végpontjait folyamatosan rajzoljuk.
1. Példa: A szakasz: (100,100,100,200), a három eltolás (dx,dy): (50,0), (20,30), (40,10).
Eltolás mellett menet közben nagyítást is alkalmazhatunk (az első végpontjából nézve s-szeresre nagyíthatunk). Ekkor a művelet első két paramétere az eltolás, harmadik paramétere pedig a nagyítás.
2. Példa: A szakasz: (100,100,100,200), a három művelet (dx,dy,s): (50,-50,2), (100,0,1), (50,0,0.75).
Végül a harmadik párhuzamosan végrehajtható művelet legyen a forgatás. Paramétere a forgatás középpontja (a szakasz mentén a szakasz első végpontjától hány szakaszhossznyira helyezkedik el: t), és a forgatás f szöge fokban, az óramutató járásával ellenkező irányban.
3. Példa: A szakasz: (100,100,100,200), a két művelet (dx,dy,s,t,f): (0,0,1,0,60), (0,0,1,1,-120).
A forgatás középpontja persze kívül is lehet a szakaszon, ekkor különlegesen érdekes ábrákat kaphatunk.
4. Példa: A szakasz: (100,150,100,200), az egyetlen művelet (dx,dy,s,t,f): (0,0,1,-1,180).
5. Példa: A szakasz: (100,100,100,200), a két művelet (dx,dy,s,t,f): (50,0,1,-0.5,60), (25,25,2,1.5,-90).
 |  |  |  |  |
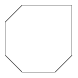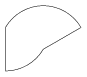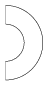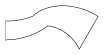| 1. Példa | 2. Példa | 3. Példa | 4. Példa | 5. Példa |
Készítsünk programot (I38.pas, ...), amely beolvassa a szakasz végpontjait, majd az N darab művelet paramétereit, majd kirajzolja a keletkezett alakzatot. (10 pont)
I. 39. A nemnegatív racionális számokat
egyértelműen felírhatjuk törtként, \(\displaystyle A\frac{b}{c}\) alakban, ahol A 
0, b 0, c>0,
b<c, valamint b és c relatív prím
(A, b, c egész számok). Ha A=0, akkor az
alak: \(\displaystyle \frac{b}{c}\), ha pedig b=0, akkor A. Készítsünk
táblázatot (I39.xls), amelyben az összeadás két operandusát beírva, az
összeget kapjuk meg.
Példa:
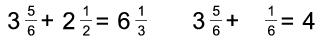
(10 pont)
A számítástechnike feladatok megoldásai a következő címre küldendők:
Cím: szamtech@komal.hu