A számítástechnika-versenyben kitűzött feladatok 2003. május

Kérjük, olvassa el a versenykiírást.

I. 52. Minden N természetes szám (1\(\displaystyle \le\)N\(\displaystyle \le\)100) felbontható \(\displaystyle N= \sum_{i=1}^kx_i\) alakban, ahol 1\(\displaystyle \le\)k\(\displaystyle \le\)N, és \(\displaystyle \forall\)i-re: x_i>0 természetes szám, valamint x_i \(\displaystyle \ge\)x_i+1.

Írjunk programot (i52.pas, ...), amely beolvassa N értékét, majd az i52.ki szöveges állományba írja az N szám 1000 darab véletlen felbontását (ugyanaz a felbontás többször is szerepelhet). Az állomány minden sorában egy-egy felírás szerepel, a felírás tagjait egy-egy szóköz választja el egymástól. A véletlen felbontásnak olyannak kell lennie, hogy bármely lehetséges felbontás azonos eséllyel kerüljön sorra.

Példa: N=5 esetén az állomány így kezdődhet:

4 1
1 1 1 1 1
3 2
5
3 2
3 1 1
...

(10 pont)

I. 53. Egy R sugarú körön, kívülről gördül egy Q sugarú kör az óramutató járásával ellentétes irányban. A gördülő körhöz kijelölünk egy, annak középpontjától A^.Q távolságra levő pontot (A\(\displaystyle \ge\)0, Q, R>0 valós szám). A kezdőállapot A=2, R=40, Q=20 esetén az ábrán látható.

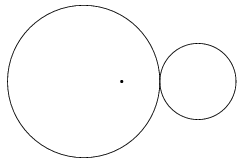
Készítsünk programot (i53.pas, ...), amely beolvassa A, F, Q, és R értékét, majd rajzolja a kijelölt pont által leírt pályát legfeljebb F (1 \(\displaystyle \le\)F \(\displaystyle \le\)100) körbeforgásig.

Példák:

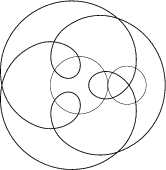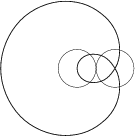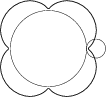A=2, R=30, Q=20	A=2, R=20, Q=20	A=0,8, R=40, Q=10

(10 pont)

I.54. Építőkockákból úgy lehet stabil tornyot építeni, hogy tetszőleges kockára csak nála kisebbet, de nagyobb sorszámút lehet tenni.

Készítsünk táblázatot (i54.xls), amely N kocka (1\(\displaystyle \le\)N \(\displaystyle \le\)10) alapján megadja a belőlük építhető legmagasabb stabil torony magasságát. (A kockák mérete pozitív egész szám.)

A táblázatban jelenjen meg a végeredményen kívül azon legmagasabb stabil tornyok magassága is, ahol legfelül az i-edik (1 \(\displaystyle \le\)i\(\displaystyle \le\)10) kocka van.

A mellékelt példában a legmagasabb toronyhoz a 2., az 5., a 6. és a 8. kockákat kell használni.

(10 pont)

A számítástechnika feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2003. június 13.