 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
I. 64. Legyen N pozitív egész szám. N-edrendű Farey-sorozatnak nevezzük a 0 és 1 közötti olyan nem egyszerűsíthető törtek növekvő sorozatát, amelyek nevezője kisebb vagy egyenlő, mint N. Például:
\(\displaystyle F_6=\frac{0}{1},\,\frac{1}{6},\,\frac{1}{5},\,\frac{1}{4},\, \frac{1}{3},\,\frac{2}{5},\,\frac{1}{2},\,\frac{3}{5},\, \frac{2}{3},\,\frac{3}{4},\,\frac{4}{5},\,\frac{5}{6},\, \frac{1}{1}. \)
Készítsünk programot (i64.pas, ...), amely beolvassa N értékét (1 \(\displaystyle \le\)N \(\displaystyle \le\)100), majd kiírja az N-edrendű Farey-sorozatot.
(10 pont)
I. 65. N+1 ismert síkbeli ponthoz (xi;yi) egy azokat szépen közelítő Bézier-görbét rajzolhatunk. A Bézier-görbe egy paraméteres görbe, ahol x-et és y-t az u paraméter függvényében fejezzük ki (0\(\displaystyle \le\)u \(\displaystyle \le\)1):
\(\displaystyle x(u)=\sum_{i=0}^nx_i{n\choose i}u^i(1-u)^{n-i},\quad y(u)=\sum_{i=0}^ny_i{n\choose i}u^i(1-u)^{n-i}. \)
Készítsünk programot (i65.pas, ...), amely beolvassa az N+1 darab pont képernyő-koordinátáit, majd kirajzolja a pontokat és a hozzájuk tartozó Bézier-görbét.
Példa:
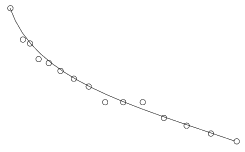
N=14
(10 pont)
I. 66. Az Euler-háromszög hasonló a Pascal-háromszöghöz, az ún. Euler számokat tartalmazza. E(n,k)-t 0 \(\displaystyle \le\)n \(\displaystyle \le\)15, 0 \(\displaystyle \le\)k \(\displaystyle \le\)n értékekre értelmezzük: E(n,k) az első n természetes szám azon permutációinak száma, amelyekben pontosan k emelkedés van, vagyis k-szor teljesül, hogy egy elem nagyobb a rákövetkező elemnél.
Készítsünk táblázatot (i66.xls), amely az A1 cellába írt m (0\(\displaystyle \le\)m\(\displaystyle \le\)15) értékre a táblázat n+1. sorába írja E(n,k) (n=0,1,...,m) értékeit. Csak az érvényes mezőkben jelenjen meg szám.
Példa m=10-re:
|
(10 pont)
A számítástechnika feladatok megoldásai a következő címre küldendők:
Cím: szamtech@komal.hu

