 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
I. 76. Készítsünk programot (i76.pas, ...) adott x természetes számra (1\(\displaystyle \le\)x\(\displaystyle \le\)500 000) azon rendezett [a;b] természetes számpárok számának meghatározására, amelyek legkisebb közös többszöröse x.
Példa:
| x=3 \(\displaystyle \to\) 3 azaz [1;3], [3;3], [3;1] |
| x=6 \(\displaystyle \to\) 9 azaz [1;6], [2;3], [2;6], [3;6], [6;6], [6;3], [6;2], [3;2] |
(10 pont)
I. 77. Tekintsük az (r;\(\displaystyle \varphi\)) polárkoordináta-rendszerben az ra=sin a\(\displaystyle \varphi\) egyenletet, ekkor ábrázolva r és \(\displaystyle \varphi\) összetartozó értékeit különböző a paraméterekre érdekes ábrákat kaphatunk. Készítsünk programot (i77.pas, ...), amely adott a paraméterrel ilyen görbét rajzol. A kép \(\displaystyle a=\frac{1}{2}\) paraméterrel készült.
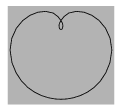
(10 pont)
I. 78. Egy nevezetes függvény Ackermann nevéhez fűződik, aki a függvények kiszámíthatóságával, bonyolultságával kapcsolatosan vizsgálódott. A róla elnevezett kétváltozós függvény különös érdekessége, hogy minden ,,normális'' függvénynél gyorsabban nő, és csak első néhány ,,tagjára'' találtak eddig zárt formulát.
Definíciója:
\(\displaystyle A(n;m)=\begin{cases} m+1,&\mbox{\ ha\ }n=0\\ A(n-1;1),&\mbox{\ ha\ $\)0$\ és\ }m=0\\ A\big(n-1;A(n;m-1)\big)&\mbox{\ ha\ $n>0$\ és\ }m>0, \end{cases} ">
ahol n és m nemnegatív egészek.
Készítsünk táblázatot (i78.xls), amely az Ackermann függvény értékeit számolja az alábbi formában (a #HIV! érték lehet ott, ahol nem tudjuk kiszámolni):
|
(10 pont)
A számítástechnika feladatok megoldásai a következő címre küldendők:
Cím: szamtech@komal.hu

