 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
I. 79. Az N-edrendű Pierce-sorozat olyan nemnegatív törtek monoton növekvő sorozatából áll, ahol a nevező értéke legfeljebb N egész szám. Az azonos értékű törtekből a nagyobb nevezőjű szerepel előbb a sorozatban. Készítsünk programot (i79.pas, ...) az M-nél nem nagyobb, N-edrendű Pierce-sorozat előállítására (1\(\displaystyle \le\)M\(\displaystyle \le\)100, 1\(\displaystyle \le\)N\(\displaystyle \le\)100).
Példa:
N=2, M=3 esetén: \(\displaystyle \frac{0}{2}\), \(\displaystyle \frac{0}{1}\), \(\displaystyle \frac{1}{2}\), \(\displaystyle \frac{2}{2},\ \frac{1}{1}\), \(\displaystyle \frac{3}{2}\), \(\displaystyle \frac{4}{2}\), \(\displaystyle \frac{2}{1}\), \(\displaystyle \frac{5}{2}\), \(\displaystyle \frac{6}{2}, \frac{3}{1}\).
(10 pont)
I. 80. Készítsünk programot (i80.pas, ...), amely beolvassa egy N-oldalú sokszög csúcsainak koordinátáit (3\(\displaystyle \le\)N\(\displaystyle \le\)100, és mindegyik koordináta 0 és 500 közötti egész szám), majd kirajzolja a sokszöget tetszőleges módszerrel háromszögekre bontva.
Példa:
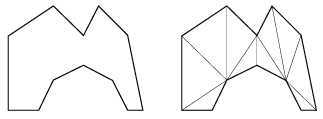
(10 pont)
I. 81. Készítsünk táblázatot (i81.xls), amely az A1 cellába írt n értékre a táblázat n+1. sorába írja a másodfajú Euler számok (E(n,k)) értékeit.
| n\k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 | ||||||||||
| 1 | 1 | 0 | |||||||||
| 2 | 1 | 2 | 0 | ||||||||
| 3 | 1 | 8 | 6 | 0 | |||||||
| 4 | 1 | 22 | 58 | 24 | 0 | ||||||
| 5 | 1 | 52 | 328 | 444 | 120 | 0 | |||||
| 6 | 1 | 114 | 1452 | 4400 | 3708 | 720 | 0 | ||||
| 7 | 1 | 240 | 5610 | 32120 | 58140 | 33984 | 5040 | 0 |
Az E(n,k) kiszámolási szabálya: Vegyük az {1,1,2,2,...,n,n} sorozat azon permutációit, ahol tetszőleges m szám két előfordulása között csak náluk nagyobb szám fordulhat elő. Az E(n,k) ezek közül azon permutációk száma, amelyekben pontosan k emelkedő részsorozat van.
(10 pont)
A számítástechnika feladatok megoldásai a következő címre küldendők:
Cím: szamtech@komal.hu

