Matematikából kitűzött gyakorlatok és feladatok
2004. szeptember

Kérjük, olvassa el a versenykiírást.

A K pontversenyben kitűzött gyakorlatok A K-jel feladatokat csak 9-edik osztályosok küldhetik be. Minden K-jelű feladat helyes megoldásáért 6 pont jár.

K. 1. A sakktáblán B8-on és G8-on áll egy-egy gyalog, B1-en pedig egy huszár. Mennyi a lehető legkevesebb lépés, amellyel le tudja ütni a huszár mindkét gyalogot? (A gyalogok eközben nem mozognak.)

Javasolta: Nagy Zoltán (Hortobágy)

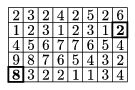
K. 2. Az ábrán megjelölt, 2-est tartalmazó mezőről el kell jutnunk a megjelölt 8-as mezőig. Minden négyzeten maximum egyszer haladhatunk át, minden mezőről a vele oldalban szomszédos mezőre léphetünk. Az így érintett számokat összegezzük. Mennyi a legnagyobb összeg, amit így kaphatunk?

K. 3. A koordinátarendszerben megadtunk egy négyszöget a csúcsaival: A(0;0), B(5;0), C(3;2), D(0;1). Mutassuk meg, hogy a négyszög átlói 45^o-os szöget zárnak be egymással.

K. 4. Határozzuk meg a p és a q (pozitív) prímszámokat, ha

p + p² + p⁴ - q - q² - q⁴ = 83 805.

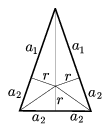
K. 5. Ha egy egyenlőszárú háromszög szögfelezőinek metszéspontjából merőlegeseket állítunk az oldalakra, a három merőleges két kisebb és egy nagyobb deltoidra bontja a háromszöget. Melyik egyenlőszárú háromszögnél lesz a két kisebb deltoid területének összege egyenlő a nagyobb deltoid területével?

K. 6. Egy szigeten kétféle ember él: jó és rossz. A jók mindig igazat mondanak, a rosszak mindig hazudnak. Természetesen mindenki vagy fiú vagy lány a szigeten. Egyszer két ember a következőket mondta kettejükre vonatkozóan:

- Ali: Rosszak vagyunk.

- Bali: Fiúk vagyunk.

Állapítsuk meg mindkettőről, hogy jó-e és hogy milyen nemű!

Javasolta: Szalkai Balázs (Veszprém)

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 770. Egy 35 fős osztály tanulói két csoportba oszthatók: a kockafejűekre és az égimeszelőkre. Az égimeszelők állítják, hogy magasabbak a kockafejűeknél, akik viszont jobb matekosnak tartják magukat. Egyikük egyszer azt kérdezte egy égimeszelőtől: ,,Mit értetek azon, hogy ti magasabbak vagytok nálunk? Talán azt, hogy

1. Minden égimeszelő magasabb valamennyi kockafejűnél?

2. A legmagasabb égimeszelő magasabb a legmagasabb kockafejűnél?

3. Minden égimeszelő magasabb valamelyik kockafejűnél?

4. Minden kockafejű alacsonyabb valamelyik égimeszelőnél?

5. A legalacsonyabb kockafejű alacsonyabb a legalacsonyabb égimeszelőnél?''

A kérdések hallatán az égimeszelő szemmel láthatóan összezsugorodott ... A feladat viszont az, hogy megállapítsuk, milyen viszonyban állnak a fenti kijelentések, azaz bármely két állítás esetén döntsük el, következik-e egyikükből a másik.

(Hugo Steinhaus nyomán)

C. 771. Matekváros és Fizikaváros különböző időzónában találhatók. Egy repülő helyi idő szerint reggel 8-kor indul Fizikavárosból, és még aznap helyi idő szerint délben érkezik Matekvárosba. A járat két óra múlva visszaindul és ugyancsak helyi idő szerint este 8 órakor érkezik Fizikavárosba. Az utazás mindkét irányban ugyanannyi ideig tart. Mennyi az idő Fizikavárosban akkor, amikor Matekvárosban dél van?

C. 772. Történt egyszer egy matematikaórán, hogy egy diák az (a+2b-3)² négyzetre emelést rosszul végezte el, és a²+4b²-9 lett az eredménye. Tanára kérésére ellenőrzésképpen behelyettesített a és b helyére egy-egy természetes számot. A behelyettesítés után az eredmény helyesnek bizonyult. Mely számokat helyettesíthette a tanuló?

C. 773. Egy trapéz alakú földdarab párhuzamos oldalai 2100 méter és 1500 méter, a szárak hossza pedig 613 méter és 37 méter. Hány négyszögöl a telek területe?

C. 774. Mekkora területű a derékszögű koordinátarendszerben azoknak a P(x;y) pontoknak a halmaza, amelyekre teljesül, hogy |x+y|+|x-y|\(\displaystyle \le\)4?

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3742. Egy 35 fős osztály tanulói két csoportba oszthatók: a kockafejűekre és az égimeszelőkre. Az égimeszelők állítják, hogy magasabbak a kockafejűeknél, akik viszont jobb matekosnak tartják magukat. Egyikük egyszer azt kérdezte egy égimeszelőtől: ,,Mit értetek azon, hogy ti magasabbak vagytok nálunk? Talán azt, hogy

1. Minden égimeszelő magasabb valamennyi kockafejűnél?

2. Több alacsonyabb kockafejű van a legalacsonyabb égimeszelőnél, mint ahány alacsonyabb égimeszelő van a legmagasabb kockafejűnél?

3. Többen vannak azok az égimeszelők, akiknél vannak alacsonyabb kockafejűek, mint azok a kockafejűek, akiknél vannak alacsonyabb égimeszelők?

4. A kockafejűek átlagmagassága kisebb az égimeszelők átlagmagasságánál?''

A kérdések hallatán az égimeszelő szemmel láthatóan összezsugorodott ... A feladat viszont az, hogy megállapítsuk, milyen viszonyban állnak a fenti kijelentések, azaz bármely két állítás esetén döntsük el, következik-e egyikükből a másik.

(4 pont)

(Hugo Steinhaus nyomán)

B. 3743. Vágjuk szét az ábrán látható paralelogrammát két részre úgy, hogy a részekből egy egységnyi élű kockát lehessen hajtogatni.

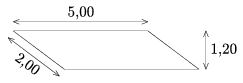
(5 pont)

Javasolta: Hajba Károly (Kisvárda)

B. 3744. Hány olyan n pozitív egész szám van, amelyre n²+10n négyzetszám?

(3 pont)

B. 3745. Az a, b, c, d számokra teljesül, hogy a+b>|c-d| és c+d>|a-b|. Bizonyítsuk be, hogy ekkor a+c>|b-d|.

(3 pont)

B. 3746. Az egyenlő oldalú ABC háromszög AB oldalán adottak az M és N pontok, a BC oldalon a P, a CA oldalon pedig a Q pont úgy, hogy

MA+AQ=NB+BP=AB.

Mekkora szöget zárhatnak be az MP és az NQ egyenesek?

(4 pont)

B. 3747. Egy háromszög oldalai a, b, c, területe \(\displaystyle \frac{(a+b+c)(a+b-c)}{4}\). Mekkora a háromszög legnagyobb szöge?

(4 pont)

B. 3748. Az ABC háromszög C csúcsából induló magasságvonal és súlyvonal harmadolják a BCA szöget. Igazoljuk, hogy a háromszög derékszögű.

(4 pont)

B. 3749. Egy téglalap oldalai 5 cm és 9 cm hosszúak. A téglalapot feldaraboljuk tíz olyan téglalapra, amelyek oldalhosszai cm-ben kifejezve egész számok. Bizonyítsuk be, hogy a darabok között van két egybevágó.

(5 pont)

B. 3750. Az {a_n} sorozatról tudjuk, hogy a₁ < a₂ pozitív egész szám, továbbá k\(\displaystyle \ge\)3 esetén a_k = 4a_k-1-3a_k-2. Igazoljuk, hogy a₄₅ > 3⁴³.

(4 pont)

B. 3751. Legyen \(\displaystyle f(x)=\frac{x}{1-x}\). Határozzuk meg a valós számok halmazának azt a legbővebb részhalmazát, ahol minden pozitív egész n esetén az

\(\displaystyle f^{(n)}(x)=\underbrace{f\big(f\big(\dots\big(f}_{n}(x)\big)\dots\big)\big) \)

összetett függvény értelmezhető.

(4 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 350. Adjuk meg az összes pozitív p egészt, melyre a 4x²+p polinom a 0,1, ...,p-1 helyeken prím értéket vesz fel.

A. 351. Legyenek a₁, a₂, ...,a_n pozitív számok, melyek összege S, szorzata P, n\(\displaystyle \ge\)3.

Bizonyítsuk be, hogy

\(\displaystyle \sum_{i=1}^n\frac{1}{S-a_i}<\sqrt[n-1]{\frac{S}{P}}. \)

A. 352. Az ABC nem egyenlő szárú háromszög körülírt köre legyen k. Az ABC háromszög C-nél levő belső szögfelezője messe a k kör B-beli érintőjét K-ban, míg a C-nél levő külső szögfelező C-től különböző metszéspontja k-val L. Legyen az AC és LB egyenesek metszéspontja M. Mutassuk meg, hogy az MK egyenes átmegy az AB oldal felezőpontján.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2004. október 15.