Matematikából kitűzött gyakorlatok és feladatok
2004. október

Kérjük, olvassa el a versenykiírást.

A K pontversenyben kitűzött gyakorlatok A K-jelű feladatokat csak 9-edik osztályosok küldhetik be. Minden K-jelű feladat helyes megoldásáért 6 pont jár.

K. 7. Hányféleképpen lehet eljutni a sakktáblán a legrövidebb úton (a legkevesebb lépéssel) C5-ről H2-re a királlyal?

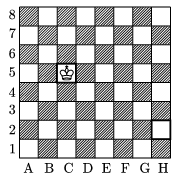
Javasolta: Gáspár Nóra (Budapest)

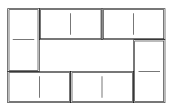
K. 8. A képen egy egyfővonalas vasútállomás vázlatos felülnézeti rajza látható. Hány különböző útvonalon haladhat át a vasútállomáson egy balról érkező vonat?

K. 9. Egy 12 cm élhosszúságú kocka alakú edényt az $\displaystyle \frac{5}{8}$ részéig megtöltöttük folyadékkal, majd az egyik éle mentén megbillentettük egy kicsit. Az ábra az edény keresztmetszetét mutatja a benne lévő folyadék vízszintjével. Tudjuk, hogy az LC szakasz hossza pontosan a KB szakasz hosszának a kétszerese. Adjuk meg az LC szakasz hosszát.

K. 10. Adjuk meg az összes olyan négyzetszámot, melynek minden számjegye páratlan.

Javasolta: Halász Tamás (Budapest)

K. 11. Az asztalra letettünk egy záródó láncba 6 különböző dominót. A dominókon összesen D pont van. Mennyi D lehetséges legkisebb értéke? (A dominók mindkét oldalán 0-6-ig mehet a pontok száma és az érintkező dominóoldalakon azonos számú pontnak kell lenni.)

K. 12. Hány pozitív egész szám írható n helyére, ha 2004ⁿ osztója 2004!-nak? [2004! jelöli 1-2004-ig az egész számok szorzatát.]

Ötlet: Englert Ákos (Zalaegerszeg)

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 775. Pistike eredeti módon számlál az ujjain. 1-gyel kezdi a hüvelykujján, ezután a 2-t és a 3-at a mutatóujján, a 4-et, 5-öt és a 6-ot a középső ujján, a 7-et a gyűrűsujján, a 8-at és 9-et a kisujján. Ezután visszafelé folytatja, a 10-et, 11-et, 12-t megint a gyűrűsujján, 13-at a középsőn, 14-et és 15-öt a mutatón, 16-ot, 17-et, 18-at a hüvelykujján, 19-et ismét visszafelé a mutatóujján és így tovább. Melyik ujján számolja a 2004-et?

C. 776. Mutassunk példát olyan derékszögű háromszögre, amely felbontható öt egybevágó háromszögre.

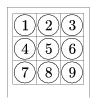
C. 777. Az özönvíz előtti jegykezelő gépek a menetjegy kilenc számozott mezője közül néhányat - akár az összeset - kilyukasztanak. A gépek beállítójától az ellenőrök azt kérik, hogy a gép ne ugyanazokat a mezőket lyukassza, ha valaki nem az előírásnak megfelelően, hanem lapjával fordítva helyezi be a jegyét. Hány ilyen beállítása lehetséges a gépnek?

C. 778. Egy számtani sorozatban jelölje S_m a sorozat első m elemének az összegét. Bizonyítsuk be, hogy minden n>k$\displaystyle \ge$1 esetén

$\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k}.$

C. 779. Egy 12x12x35 cm-es, 5 kg tömegű gépsonkát ferdén vágtunk el úgy, hogy a paralelogramma alakú metszet oldalhosszúsága 15 és 20 cm. Mekkora lehet a keletkezett két darab tömege?

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3752. Mutassuk meg, hogy ha egy konvex nyolcszög szemközti oldalai párhuzamosak és egyenlők, akkor a sokszög feldarabolható paralelogrammákra.

(3 pont)

B. 3753. Jelölje S_m az (a_m) sorozat első m elemének az összegét. Bizonyítsuk be, hogy ha minden n$\displaystyle \ne$k pozitív egészre teljesül, hogy

$\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k},$

akkor (a_m) számtani sorozat.

(3 pont)

B. 3754. Bizonyítsuk be, hogy a szabályos háromszög nem bontható föl öt egybevágó háromszögre.

(5 pont)

B. 3755. Egy kör úgy metszi egy konvex négyszög oldalait egy-egy szakaszban, hogy a négyszög belsejébe eső szemközti körívek hosszának összege egyenlő. Bizonyítsuk be, hogy a négyszög húrnégyszög.

(4 pont)

B. 3756. A nyolcjegyű számokat osszuk két halmazba. Az egyik halmazba kerüljenek azok, amelyek felbonthatók két négyjegyű szám szorzatára, a másikba azok, amelyek nem. Melyik halmazba kerül több szám?

(5 pont)

B. 3757. A k₁ és a k₂ körök az A és a B pontokban metszik egymást, egyik közös érintőjük pedig az E₁, illetve az E₂ pontokban érinti a köröket. Bizonyítsuk be, hogy az A, E₁, E₂, illetve a B, E₁, E₂ pontokon átmenő körök sugara egyenlő.

(4 pont)

B. 3758. Legyen az n pozitív páros szám. Írjuk az 1,2,...,n² számokat egy nxn-es táblázat mezőibe úgy, hogy a táblázat k-adik sorában az elemek balról jobbra olvasva rendre (k-1)n + 1, (k-1)n + 2, ..., (k-1)n + n legyenek (k = 1,2,...,n).

Színezzük ki az így kitöltött táblázat mezőit bordó és sárga színnel úgy, hogy minden sorban és minden oszlopban a mezők fele bordó, a másik fele pedig sárga legyen. (A sakktábla-szerű színezés például egy lehetőség.) Bizonyítsuk be, hogy minden ilyen színezésre a bordó és a sárga mezőkön lévő számok összege egyenlő.

(4 pont)

B. 3759. Bizonyítsuk be, hogy minden k pozitív egész számra (2k)! osztható k!^.(k+1)!-sal.

(4 pont)

B. 3760. Az ábrán látható téglatestben az EH él felezőpontja S, a HG él felezőpontja R és a GF él felezőpontja Q. Bizonyítsuk be, hogy az ASR és a DRQ háromszögek területe egyenlő.

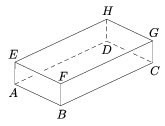
(4 pont)

B. 3761. Oldjuk meg az alábbi egyenletrendszert:

$\displaystyle \frac{1}{x}+\frac{1}{2y}=(x^2+3y^2)(3x^2+y^2),$

$\displaystyle \frac{1}{x}-\frac{1}{2y}=2(y^4-x^4).$

(5 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 353. Bizonyítsuk be, hogy a $\displaystyle 2^{2^n}+1$ és $\displaystyle 6^{2^n}+1$ sorozatok együttvéve végtelen sok összetett számot tartalmaznak.

A. 354. Bizonyítsuk be, hogy

$\displaystyle 2+ \frac{1}{1+\cfrac{1}{2+\cfrac{2}{3+\cfrac{3}{4+\cfrac{4}{5+\dots}}}}}=e.$

A. 355. Az MO űrvárosban 100 űrállomás van. Bármely kettőt alagút köt össze. Az alagutak közül 100-ban kétirányú, a többiben egyirányú a közlekedés. 4 űrállomást szorosan kapcsolódónak nevezünk, ha bármelyikükről eljuthatunk a többi háromba a 4 állomás közti alagutakon keresztül. Tervezzük meg az MO várost úgy, hogy abban a lehető legtöbb szorosan kapcsolódó négyes legyen. Adjuk meg a maximumot, és bizonyítsuk is be.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő:

A K-jelű feladatoknál 2004. november 10.,

Az A-, B- és C-jelű feladatoknál 2004. november 15.,