!--#set var="TITLE" value="A 2004. decemberi B-jelű matematika feladatok megoldása" -->

A 2004. decemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3772. Hány olyan (n;k) számpár van, amelyre n>k, továbbá az n és k oldalú szabályos sokszögek belső szögének az eltérése 1^o?

(4 pont)

Megoldás: Mivel a belső szögek eltérése megegyezik a külső szögek eltérésével, a második feltétel ekvivalens a

$\displaystyle {360\over k}-{360\over n}=1$

feltétellel, amit ekvivalens átalakításokkal

360n-360k=nk, (360-k)(360+n)=360²

alakra hozhatunk. A k és n számokra további feltételeink: 3$\displaystyle \le$k$\displaystyle \le$n. Mivel (360-k)(360+k)<360², a (360-k)(360+n)=360² feltétel teljesülése esetén k<n automatikusan teljesülni fog. Minden 360²=a^.b alakú előállítás, ahol a,b pozitív egész számok és a$\displaystyle \le$357, megfelel tehát egy alkalmas (n,k) számpárnak, ahol k=360-a és n=b-360, és az is világos, hogy minden megfelelő számpárt megkapunk ilyen módon. Mivel pedig sem 358, sem 359 nem osztója a 360² számnak, az a,b pozitív egészekre adott feltétel ekvivalens az a<b feltétellel.

A 360²=2⁶^.3⁴^.5² prímtényezős felbontás alapján látható hogy 360² pozitív osztóinak száma (6+1)(4+1)(2+1)=105. Ezért a 360² számot, nagyságrendi megkötések nélkül, éppen 105 féleképpen lehet a^.b alakban felírni, ahol a,b pozitív egész számok. Ebből a 360^.360 előállítás nem lesz megfelelő, a többi 104 előállításnak pedig pontosan felében fog teljesülni az a<b feltétel. A szóban forgó (n,k) számpárok száma tehát 52.

B.3773. Osztható-e

20²⁰⁰⁴+16²⁰⁰⁴-3²⁰⁰⁴-1

323-mal?

(3 pont)

Megoldás: Mivel 323=17^.19, vizsgáljuk meg azt, hogy az adott szám osztható-e 17-tel, illetve 19-cel. Ismeretes, hogy ha a és b különböző egész számok, n pedig természtes szám, akkor aⁿ-bⁿ osztható (a-b)-vel. Ebből az is következik, hogy ha a² és b² is különböző, továbbá n páros, akkor aⁿ-bⁿ osztható (a²-b²)-tel, következésképpen (a+b)-vel is.

Ezt alkalmazva látható, hogy

17 | 20²⁰⁰⁴-3²⁰⁰⁴, 17 | 16²⁰⁰⁴-1²⁰⁰⁴, 19 | 20²⁰⁰⁴-1²⁰⁰⁴, 19 | 16²⁰⁰⁴-3²⁰⁰⁴.

Vagyis a szóban forgó szám osztható mind 17-tel, mind 19-cel. Mivel 17 és 19 relatív prímek, a szám a szorzatukkal, 323-mal is osztható.

B.3774. Az egyenlő szárú derékszögű ABC háromszög AB átfogóján adottak a K és az M pontok. K az A és az M között van, továbbá KCM$\displaystyle \angle$=45^o. Bizonyítsuk be, hogy AK²+MB²=KM².

(3 pont)

Megoldás: Legyen az A illetve B pontok tükörképe a CK illetve CM egyenesre rendre A' és B'. Mivel az ACK és BCM szögek összege 45^o, az ACA' és BCB' szögek összege 90^o lesz. Mivel pedig CA'=CA=CB=CB', az A' és B' pontok egybeesnek. Mivel a CKA=CKA' és CMB=CMB' szögek a KMC háromszög egy-egy szögét egészítik ki 180^o-ra, összegük éppen 180^o-kal lesz nagyobb a KMC háromszög harmadik, 45^o-os szögénél. A CKA'M négyszög A'-nél lévő szöge tehát derékszög, vagyis a Pithagorasz-tétel szerint

AK²+MB²=A'K²+A'M²=KM².

B.3775. Oldjuk meg az

y³=x³+8x²-6x+8

egyenletet a nemnegatív egészek körében.

(4 pont)

Megoldás: Ha x>9, akkor 2x²>18x, tehát

(x+2)³=x³+6x²+12x+8<x³+8x²-6x+8.

Másrészt tetszőleges nemnegatív x szám esetén

x³+8x²-6x+8<x³+9x²+27x+27=(x+3)³.

Ezért x>9 esetén az x³+8x²-6x+8 szám két egymást követő pozitív egész szám harmadik hatványa közé esik, így nem lehet köbszám. A 9-nél nem nagyobb nemnegatív egész számokat megvizsgálva pedig azt tapasztaljuk, hogy az x³+8x²-6x+8 szám csak x=0 és x=9 esetén lesz köbszám. Az egyenlőségnek tehát két nemnegatív egész számpár tesz eleget: x=0, y=2 és x=9, y=11.

B.3776. Az ABCD húrnégyszög BD átlója egyben a körülírt kör átmérője. Az ABC háromszög oldalainak a hossza legalább 1. Bizonyítsuk be, hogy a négyszög területe nagyobb, mint $\displaystyle \frac{1}{2}$ területegység.

(4 pont)

Klein Eszter és Terry Tao (Sidney, Ausztrália)

Megoldás: Thalész tétele miatt az ABD és CBD háromszögek A illetve C csúcsánál derékszög van. A négyszög T területe e két háromszög területének összege. Felhasználva, hogy AB,AC,BC$\displaystyle \ge$1, a háromszög egyenlőtlenség miatt

$\displaystyle T={1\over2}(AB\cdot AD+BC\cdot CD)\ge{1\over2}(AD+CD${1\over2}AC\ge {1\over2}.">

B.3777. Az ABC egyenlő szárú háromszög szárszöge BAC$\displaystyle \angle$=$\displaystyle \alpha$. A BC alapot B-től C felé haladva n egyenlő részre osztó pontok D₁, D₂,..., D_n-1. Az AB szárat 1:(n-1) arányban osztó pont E. Igazoljuk, hogy

$\displaystyle AD_1E\sphericalangle+AD_2E\sphericalangle+\dots+AD_{n-1}E\sphericalangle= \frac{\alpha}{2}. $

(4 pont)

Megoldás: Jelölje i=1,2,..., n-1 esetén a BAD_i, AD_iE és BED_i szögeket redre $\displaystyle \alpha$_i, $\displaystyle \delta$_i, $\displaystyle \varepsilon$_i. Egy háromszög két belső szögének összege egyenlő a harmadik csúcsnál lévő külső szöggel. Ezt az AD_iE háromszögre alkalmazva az $\displaystyle \alpha$_i+$\displaystyle \delta$_i=$\displaystyle \epsilon$_i összefüggést kapjuk, ahonnan

$\displaystyle \sum_{i=1}^{n-1}AD_iE\measuredangle=\sum_{i=1}^{n-1}\delta_i= \sum_{i=1}^{n-1}\varepsilon_i-\sum_{i=1}^{n-1}\alpha_i.$

A párhuzamos szelők tétele miatt a BED_n-1 háromszög hasonló a BAC háromszöghöz, tehát egyenlőszárú és szárszöge $\displaystyle \varepsilon$_n-1=$\displaystyle \alpha$. A háromszögek és a felosztás szimmetriája miatt 1$\displaystyle \le$i$\displaystyle \le$n-2 esetén felírhatók az

$\displaystyle \varepsilon$_i+$\displaystyle \varepsilon$_n-1-i=$\displaystyle \alpha$

és 1$\displaystyle \le$i$\displaystyle \le$n-1 esetén az

$\displaystyle \alpha$_i+$\displaystyle \alpha$_n-i=$\displaystyle \alpha$

egyenlőségek, ahonnan

$\displaystyle \sum_{i=1}^{n-2}\varepsilon_i={n-2\over2}\alpha,\quad\sum_{i=1}^{n-1}\alpha_i={n-1\over2}\alpha.$

Megállapításainkat összegezve,

$\displaystyle \sum_{i=1}^{n-1}AD_iE\measuredangle=\sum_{i=1}^{n-2}\varepsilon_i+ \varepsilon_{n-1}-\sum_{i=1}^{n-1}\alpha_i= {n-2\over2}\alpha+\alpha-{n-1\over2}\alpha={\alpha\over2},$

ahogyan azt bizonyítanunk kellett.

B.3778. Az ABCD konvex négyszög átlói az E pontban metszik egymást. Igazoljuk, hogy

$\displaystyle \big|t(ABE\triangle)-t(CDE\triangle)\big|\le\frac{1}{2}AD\cdot BC. $

(4 pont)

Megoldás: Az E pontból az A,B,C,D csúcsokba mutató vektorokat jelölje rendre a, b, c és d. Ekkor az axb és cxd vektorok iránya megegyezik, hosszuk pedig rendre az ABE illetve CDE háromszögek területének kétszeresével egyenlő. Vagyis

2|t( ABE$\displaystyle \Delta$) - t( CDE$\displaystyle \Delta$)| = |axb-cxd|.

Mivel az a és c vektorok párhuzamosak, axc=0, és ugyanígy dxb is a nullvektor lesz. Ezért

$\displaystyle AD\cdot BC\ge\left|\overrightarrow{AD}\times\overrightarrow{BC}\right| =\left|(d-a)\times(c-b)\right|=\left|d\times c-a\times c-d\times b+a\times b\right|= \left|a\times b-c\times d\right|,$

bizonyítva az állítást.

B.3779. Tekintsük azokat a síkokat, amelyek a 2 egység élű kocka egy-egy csúcsából kiinduló élek felezőpontján mennek át. Mekkora a síkok által határolt konvex test térfogata?

(3 pont)

Megoldás: A síkok a kocka minden egyes csúcsából levágnak egy-egy egymásba nem nyúló tetraédert. Egy ilyen tetraédernek három egy csúcsban összefutó egymásra merőleges éle egységnyi hosszú, a tetraéder térfogata tehát 1/6. A megcsonkított kocka térfogata tehát 8-8(1/6)=40/6 egységnyi.

Tekintsük most az eredeti kocka egy lapját (mondjuk a felső lapot, amenynyiben a kockát az egyik lapjára állítottuk), ebből a síkok egy olyan négyzetet vágnak ki, melynek csúcsai a lap éleinek felezőpontjai; e négyzet területe fele a lap területének, tehát 2 egységnyi. A négyzet tetszőleges e élét kiválasztva, az arra illeszkedő elvágó S sík áthalad a négyzetlap középpontja fölött 1 egység távolságra elhelyezkedő ponton. Ezt úgy láthatjuk be, hogy tekintjük a kockának azt az élközéppontját, mely az S síkra illeszkedik és az e éllel egy szabályos háromszöget alkot. Ezt a pontot az e él egyenesére tükrözve kapjuk az előbb említett pontot, mely nyilván illeszkedik az S síkra. Az elvágó síkok a kocka felső lapjával együtt tehát egy olyan négyzet alapú egyenes gúlát határoznak meg, melynek alapterülete 2 egységnyi, magassága 1 egységnyi, térfogata pedig ennek megfelelően 2/3.

A síkok által határolt test (mely egyébként egy szabályos oktaéder lesz) térfogatát tehát megkapjuk, ha a megcsonkított kocka térfogatához hozzádjuk a kocka lapjaira emelt hat kis gúla térfogatát. Az eredmény ezek szerint

$\displaystyle {40\over6}+6\cdot{2\over3}={64\over6}.$

B.3780. Igazoljuk, hogy az x, y, z pozitív számokra teljesül az alábbi egyenlőtlenség:

$\displaystyle \frac{x+y+z}{\sqrt[3]{xyz}}\le\frac{x}{y}+\frac{y}{z}+\frac{z}{x}. $

(5 pont)

Elemente der Mathematik, Basel

Megoldás: Az $\displaystyle a=x/\root3\of{xyz}$, $\displaystyle b=y/\root3\of{xyz}$, $\displaystyle c=z/\root3\of{xyz}$ helyettesítéssel az a,b,c pozitív számokra abc=1 teljesül, egyenlőtlenségünk pedig az

$\displaystyle {a\over b}+{b\over c}+{c\over a}\geq a+b+c$

alakot ölti. Az általánosság megszorítása nélkül feltehető, hogy a három szám közül a a legnagyobb, b pedig a legkisebb; ekkor a$\displaystyle \ge$1$\displaystyle \ge$b és $\displaystyle \alpha$=ab$\displaystyle \le$a. Elvégezve a c=1/ab helyettesítést, egyenlőtlenségünk így alakítható:

$\displaystyle {a\over b}+ab^2+{1\over a^2b}\ge a+b+{1\over ab},$

vagy ami ezzel ekvivalens:

a³+a³b³+1$\displaystyle \ge$a³b+a²b²+a.

Az $\displaystyle \alpha$=ab helyettesítéssel tehát az

a³+$\displaystyle \alpha$³+1-$\displaystyle \alpha$a²-$\displaystyle \alpha$²-a$\displaystyle \ge$0

egyenlőtlenséget kell igazolnunk. Itt a baloldali kifejezést

(a²-1)(a-$\displaystyle \alpha$) + ($\displaystyle \alpha$²-1)($\displaystyle \alpha$-1)

alakra hozahtjuk. Az a$\displaystyle \ge$1 és a$\displaystyle \ge$ $\alpha$ egyenlőtlenségek miatt (a²-1)(a- $\alpha$ ) $\ge$ 0, ahol egyenlőség a=1 vagy a= $\alpha$ esetén áll fenn. Továbbá

( $\alpha$ ²-1)( $\alpha$ -1)=( $\alpha$ -1)²( $\alpha$ +1) $\ge$ 0,

itt egyenlőség $\alpha$ =1 esetén áll fenn.

Ezzel az egyenlőtlenséget igazoltuk. Egyenlőség esetén szükségképpen $\alpha$ =1, ahonnan a=1 is adódik, ebből pedig b=1, majd c=1 is következik. Mivel ekvivalens átalakításokat hajtottunk végre, az eredeti egyenlőtlenségben x=y=z esetén állhat csak fenn egyenlőség, amikor is mindkét oldal értéke 3-mal egyenlő.

B.3781. Határozzuk meg a 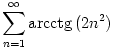$\sum_{n=1}^{\infty}\mathop{\rm arcctg}\,(2n^2)$ összeg értékét.

(5 pont)

Megoldás: Legyen $\alpha$ _n=arcctg(2n²), ekkor 0< $\alpha$ _n< $\pi$ /4 és tan $\alpha$ _n=1/2n². Legyen $\alpha$ ₁+ $\alpha$ ₂+...+ $\alpha$ _n= $\beta$ _n. Ekkor tan $\beta$ ₁=1/2, és a tangens függvény addíciós képlete segítségével tan $\beta$ _n néhány további értékét is kiszámíthatjuk: tan $\beta$ ₂=2/3, tan $\beta$ ₃=3/4, tan $\beta$ ₄=4/5. Tegyük fel tehát, hogy n $\ge$ 2 és a tan $\beta$ _n-1=1-1/n összefüggést már igazoltuk. Ekkor

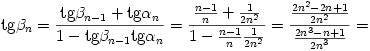
$\tan\beta_n= {\tan\beta_{n-1}+\tan\alpha_n\over1-\tan\beta_{n-1}\tan\alpha_n}= {{n-1\over n}+{1\over2n^2}\over1-{n-1\over n}{1\over2n^2}}= {{2n^2-2n+1\over2n^2}\over{2n^3-n+1\over2n^3}}=$

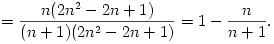
$={n(2n^2-2n+1)\over(n+1)(2n^2-2n+1)}=1-{n\over n+1}.$

A teljes indukció elve szerint tehát minden n pozitív egész számra tan $\beta$ _n=1-1/(n+1). Tudjuk továbbá, hogy 0< $\beta$ ₁< $\pi$ /4. Ha n $\ge$ 2 és 0< $\beta$ _n-1< $\pi$ /4, akkor 0< $\beta$ _n= $\beta$ _n-1+ $\alpha$ _n< $\pi$ /2 és tan $\beta$ _n<1 miatt 0< $\beta$ _n< $\pi$ /4 is teljesül. A $\beta$ _n sorozat összes eleme tehát 0 és $\pi$ /4 közé esik, továbbá tan $\beta$ _n szigorúan növekedő módon 1-hez tart. Minthogy pedig a tangens függvény a (0, $\pi$ /2) intervallumban szigorúan monoton növekedő folytonos függvény, megállapíthatjuk, hogy a $\beta$ _n sorozat határértéke 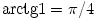$\arctan1=\pi/4$ . A feladatban szereplő végtelen összeg tehát konvergens, értéke pedig /4-gyel egyenlő.