 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
Az I pontversenyben kitűzött gyakorlatok
I. 94. Kísérletezzünk, gondolkozzunk!
Készítsünk programot, amely a futás elején bekéri az a paraméter értékét (valós szám), majd megjeleníti a képernyőn az (x2+y2)2=(x+ay) x2 egyenletű síkgörbét. Ügyeljünk a képernyőn való ,,szép'' megjelenítésre. Demo verzióval mutassunk példát az a paraméter ,,érdekes'' értékeire is.
Beküldendő a program (i94.pas).
(10 pont)
I. 95. Egy összefüggő számítógépes hálózat csomópontokból és csomópontpárokat összekötő kábelekből áll. Ezt biztonságosabbá szeretnénk tenni, vagyis olyanná, hogy ha a kábelek bármelyike (de csak az egyike!) elszakad, a hálózat attól még összefüggő maradjon. Adjunk meg minél kevesebb csomópontpárt, melyek közé kábelt téve a hálózat biztonságosabbá válik.
Az egyes csomópontokat pozitív egész számokkal jelöljük. A program olvassa be a csomópontpárokat megadó számpárokat, soronként két egész számot, szóközzel elválasztva. A beolvasás végét két nulla jelzi, szintén szóközzel elválasztva. Ugyanilyen formátumban írja ki a képernyőre a szükséges kábeleket jellemző csomópontpárokat.
Fontos! A megoldást programmal fogjuk ellenőrizni, úgyhogy semmi mást ne írjon ki a képernyőre, és ne tegye lapozhatóvá a kimenetet!
(Tipp: teszteléshez átirányíthatjuk az stdin-t).
Beküldendő a program (i95.pas).
(10 pont)
I. 96. Egy sorozat első n tagja nem határozza meg a sorozat többi tagját: bárhogyan folytathatjuk a tagok felsorolását.
Mi most az (n+1)-edik tag meghatározására a következő eljárást írjuk elő (n \(\displaystyle \ge\)2 legyen pozitív egész szám):
Képezzük a szomszédos tagok különbségét úgy, hogy a nagyobb indexűből kivonjuk a kisebb indexűt. A kapott különbségsorozattal ismét elvégezzük ezt az eljárást.
Néhány lépés után konstans sorozatot kapunk, amelyben már nincsenek különböző tagok. Ez legkésőbb az (n-1)-edik lépésben bekövetkezik, mert annak egyetlen tagja van. Például (most még csak a nagyobb méretű, sötétebb számokat nézzük!):
| 1 | 4 | 9 | 16 | 25 | 36 | 1 |
| 3 | 5 | 7 | 9 | 11 | 1 | |
| 2 | 2 | 2 | 2 | |||
| 1 | 2 | 6 | 17 | 39 | ||
| 1 | 4 | 11 | 22 | |||
| 3 | 7 | 11 | ||||
| 4 | 4 |
Ekkor előírjuk, hogy az (n+1)-edik tagot úgy kell megállapítani, hogy ismét elvégezve az eljárást, a konstans sorozat továbbra is konstans sorozat maradjon. Ebből a konstansból visszafelé lépegetve készítsük el az (n+1)-edik tagot. (Ezt mutatják példáinkon a kisebb méretű, világosabb számok.)
Készítsünk táblázatot (i96.xls), amely egy sorozat első n tagjához a most adott eljárással megkeresi a megfelelő (n+1)-edik tagot.
Beküldendő a táblázat (i96.xls). Szükség esetén az első mezőbe (A1) beírhatjuk a használati utasítást.
(10 pont)
Felhívjuk versenyzőink figyelmét a versenykiírásban közölt formai követelmények pontos betartására (megjegyzések, ADATOK)!
Az I-jelű feladatok megoldásai a következő címre küldendők:
i@komal.hu
Az S pontversenyben kitűzött feladat
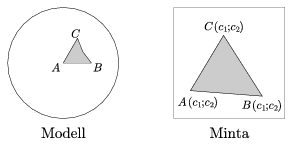
S. 5. Írjunk programot Escher-szerű hiperbolikus csempézések készítésére. (Lásd cikkünket.) A program csempézze ki a körmodellt háromszögekkel, és mindegyik csempébe rajzoljon be egy mintát, amit egy külön fájlban adunk meg.
A program bemenete a következő elemekből áll:
\(\displaystyle \frac1p+\frac1q+\frac1r<1. \)
A kiinduló ABC csempeháromszöget úgy kell elhelyezni, hogy az A csúcs a modell középpontja legyen, a B csúcs pedig ettől vízszintesen jobbra helyezkedjen el (lásd az ábrát).
A program az adatokat a parancssorból vegye a következő sorrendben:
(programnév) p q r csempeminta.ppm a1 a2 b1 b2 c1 c2 output.ppm m
(A csempeminta.ppm és az output.ppm helyén természetesen más fájlnevek fognak állni.) A program a megadott adatok alapján készítse el a szintén PPM formátumú képfájlt. A minta rajzolásakor a cikkben leírt súlyponti koordinátás módszert alkalmazza.
(10 pont)
Amit a PPM formátumról tudni kell
A feladatbeli program inputja és outputja is színes, bináris PPM típusú fájl, a kép mérete legfeljebb 2048×2048.
Fejléc (header)
A fájl a fejléccel kezdődik. A fejléc 4 adatból áll:
- A "P6" szó, ami a fájl első két bájtján áll;
- A kép szélessége és magassága;
- A szín értékek maximuma (1--255).
Ez a négy adat ebben a sorrendben, szóközökkel, soremelésekkeL (CR, LF) és TAB karakterekkel van elválasztva egymástól.
A fejléc tartalmazhat megjegyzéseket is. A megjegzyzés tetszőleges helyen kezdődhet, az első karaktere mindig # és a sor végéig tart.
A fejléc az utolsó adat utáni első LF karakterig tart.
Bináris adat
A fejléc után követkenek a pixelek adatai. A pixelek soronként vannak felsorolva, felülről lefelé, balról jobbra.
Minden pixel három bájtból áll, ezek a piros (R), zöld (G), illetve kék (B) értékeket tartalmazzák.
Az S-jelű feladatok megoldásai a következő címre küldendők:
s@komal.hu

