Kifordítható tetraéder

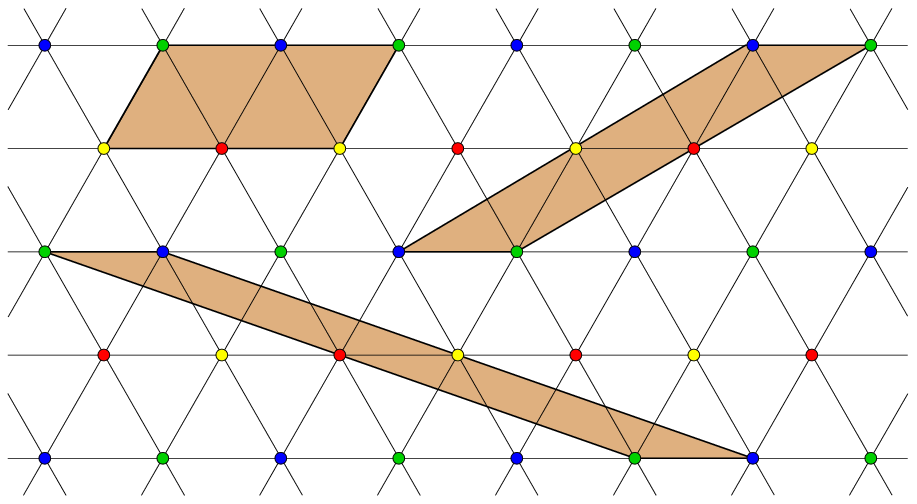
Ha a szabályos tetraédert sík felületen görgetjük, a csúcsai és a lapjai háromszögrácsot járnak be. (Ez azon múlik, hogy a tetraéder csúcsainál a szögek összege éppen 180^o.) A rácsban sok helyen felfedezhetjük a kiterített tetraédert; például bármelyik sávban, amit párhuzamos rácsegyenesek határolnak, a sáv kétszeres periódusa kiadja a test teljes felszínét.

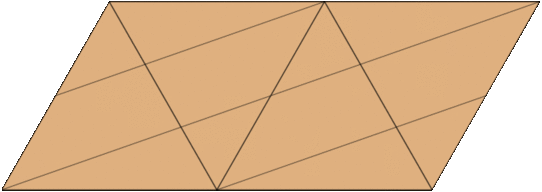
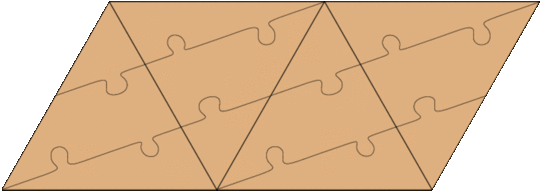
Ha a kétszeres periódus határát rárajzoljuk a tetraéder felszínére, egy zárt, állandó szélességű szalagot kapunk. Ha a szalag elég keskeny, akkor az élek mentén hajtogatva ki is fordíthatjuk, és a kifordított szalagot újra tetraéderfelszínné hajtogathatjuk össze. (Célszerű lehet a szalag szélén füleket is kialakítani.)

Elszánt, a Bolyai-geometriában jártas Olvasóink megpróbálkozhatnak a kifordítható focilabda megtervezésével és elkészítésével is.

Kós Géza