A parabola

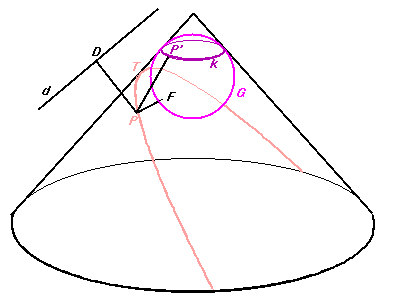
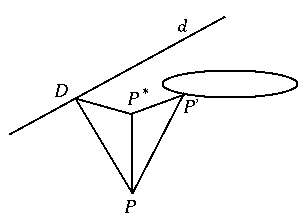
Legyen P a síkmetszet egy tetszőleges pontja. Illesszünk a kúpba egy olyan érintőgömböt G, ami egyúttal a síkot is érinti. A kúpot k körben, a síkot F pontban érinti G. P-ből a Dandelin-gömbhöz húzott érintőszakaszok PF és PP', amik egyenlő hosszúságúak. A metszősík és k síkja d egyenesben metszik egymást. P-ből merőlegest állítva d-re és k síkjára kapjuk D és P^* talppontokat. PD a metszősíkban van és párhuzamos azzal az alkotóval, amivel a sík is párhuzamos. Így a DPP^* és a P^*PP' szög is váltószöge egy-egy olyan szögnek, melynek egyik szára a kúp tengelye, másik szára pedig egy alkotó; a két szög tehát egyenlő. Ezért a kapott PP'P^* derékszögű háromszög egybevágó a PP^*D derékszögű háromszöggel (egy oldaluk közös és a rajta fekvő szögeik egyenlőek). Tehát az átfogók egyenlő hosszúak: DP=PP', másrészről PP'=PF. Összefoglalva elmondható, hogy a síkmetszet pontjai egy adott ponttól (fókusz) és egy adott egyenestől (direktrix/vezéregyenes) egyenlő távolságra vannak, a síkmetszet ezért egy parabola.

Vissza a főoldalra