A 2002. évi Eötvös-verseny

2002. október 18-án rendezte meg az Eötvös Loránd Fizikai Társulat Budapesten és 14 vidéki városban az ezévi Eötvös-versenyt. A versenyen 169 magyar, 1 szlovák és 1 román állampolgárságú versenyző adott be dolgozatot, nevezetesen Budapesten 64, Szegeden 19, Pécsett 17, Debrecenben és Szekszárdon 10-10, Veszprémben 9, Nagykanizsán és Sopronban 8-8, Békéscsabán 7, Egerben 5, Győrött 5, Miskolcon 4, Székesfehérváron 3, Nyíregyházán és Szombathelyen pedig 1-1 dolgozat született. A versenyzők 92%-a gimnazista volt; az érettségizett versenyzők valamennyien budapesti egyetemeken (BMGE, ELTE) tanulnak. Ismertetjük a feladatokat, s azok helyes megoldását.

1. Szeretnénk megbecsülni, hogy mekkora erő feszíti a gyűrűn edző tornász karjait pályájának legalsó pontján, ha kézenállásból óriáskörbe lendül. A következő egyszerű modellt alkalmazzuk: igen hosszú, nyújthatatlan kötél végére l hosszúságú, m tömegű homogén rudat erősítünk, és az 1.a ábrán látható helyzetből elengedjük. Számítsuk ki, hogy mekkora erő feszíti a kötelet az 1.b ábrán látható pillanatban! (A kötél tömegét hanyagoljuk el!)

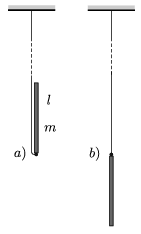
1. ábra

(Takács Gábor feladata nyomán)

Megoldás. Az eldőlő rúdra két erő hat: az mg nehézségi erő és a K kötélerő (2. ábra). Mindkettő függőleges irányú (a változó nagyságú kötélerő azért, mert a kötél ,,igen hosszú''). Mivel csak függőleges erők hatnak a rúdra, ezért a tömegközéppontja is csak függőleges, egyenes vonalú pályán mozoghat, tehát függőleges (nem harmonikus) rezgőmozgást végez.

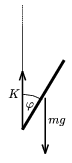
2. ábra

A rúd alsó (a kötéllel érintkező) végének függőleges irányú elmozdulása a mozgás során mindvégig zérus, ez a pont tehát függőlegesen nem gyorsul. A kérdezett állapotban a tömegközéppont sebessége zérus, gyorsulása pedig maximális és akkora, amekkora nagyságú a rúd végeinek gyorsulása a tömegközéppont vonatkoztatási rendszerében:

$\displaystyle a=\frac{l}{2}\,\omega^2. $

A munkatétel szerint:

$\displaystyle mgl=\frac12\left(\frac1{12}ml^2\right)\omega^2, $

továbbá a dinamika alaptörvénye szerint:

$\displaystyle K-mg=m\frac{l}2\omega^2. $

E két egyenletből következik: K=13 mg.

Megjegyzések. 1. Az eredményül kapott erő hihetetlenül nagy! Még akkor is, ha figyelembe vesszük, hogy a tornász egy karját ekkora erőnek csak a fele feszítené. Nem csoda, hogy olyan sok versenyző elhitte a feladat egyik tipikusan hibás feltételezésével, a kötél mozdulatlannak vélt alsó végpontja körüli forgásból kapható K=4 mg (hibás) végeredményt.

Nem sokkal az Eötvös-verseny után volt Debrecenben a 2002. évi tornász világbajnokság, amelyet gyűrűn - mint ismeretes - Csollány Szilveszter nyert meg. Az ő gyakorlatát alaposan megfigyelve jól lehetett látni, hogy a feladatban használt modell mennyire durva közelítése a merev testnek aligha tekinthető tornász mozgásának.

2. A feladat ugyan nem kérdezte, de tanulságos kiszámítani a kötelet feszítő erőt a rúd tetszőleges, mondjuk a függőlegessel $\displaystyle \varphi$ szöget bezáró helyzetében is. A fentiekhez hasonló számolásból (munkatétel + mozgásegyenlet) adódik:

$\displaystyle K(\varphi)=\frac{3{(\cos\varphi-1)}^2+1}{{(3\sin^2\varphi+1)}^2}\,mg. $

Ez a kifejezés sehol nem nulla (3. ábra), tehát a kötél nem lazul meg, jóllehet $\displaystyle \varphi$ $\approx$ 61^o-nál K alaposan (mg egyhatodára) lecsökken.

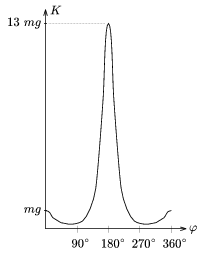
3. ábra

2. Zárt lombikban egy kevés víz van. A lombik száját lefelé fordítva a víz kb. 5 cm magasan áll a lombik nyakában. (A belső méreteket a 4. ábra mutatja.)

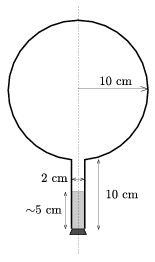
4. ábra

Ezután a lombikot függőleges tengelye körül egyenletes forgásba hozzuk úgy, hogy másodpercenként hármat forduljon. Gondoskodunk róla, hogy a lombik falának hőmérséklete mindenütt ugyanakkora legyen. Kellően hosszú idő után egyensúly áll be.

Rajzoljuk fel vázlatosan, hogyan helyezkedik el ekkor a víz a lombikban!

(Károlyházy Frigyes)

Megoldás. A feladat első ránézésre mechanikai problémának látszik. Ki fog derülni, hogy legalább ennyire termodinamikai feladat is; az egyensúly, ami ,,kellően hosszú idő után'' beáll, termodinamikai egyensúly lesz. A példa termodinamikai jellegére utal a lombik falának hőmérsékletéről szóló mondat is.

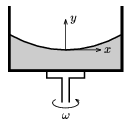
5. ábra

Az egyenletes forgásba hozott folyadék felszíne a földi homogén nehézségi erőtérben forgásparaboloid. Ennek síkmetszetét mutatja az 5. ábra. A ,,megforgatott parabola'' egyenlete az ábrán felvett koordináta-rendszerben

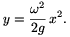
$y=\frac{\omega^2}{2g}\,x^2.$

Megjegyzések. 1. A fenti összefüggést annak alapján határozhatjuk meg, hogy a folyadék az $\omega$ szögsebességgel forgó koordináta-rendszerben egyensúlyban van; felülete a ráható erők eredőjére merőleges. Így az érintő iránytangense

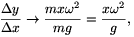
$\frac{\Delta y}{\Delta x}\to\frac{mx\omega^2}{mg}= \frac{x\omega^2}{g},$

amiből [minthogy y(0)=0] a megadott formula következik.

2. Úgy is megkaphatjuk a felület egyenletét, hogy felismerjük: egy m tömegű folyadékdarabkára ható centrifugális erő kifejezése hasonló a Hooke-törvényben szereplő rugóerő képletéhez, de a ,,rugóállandó'' negatív, D=-m $\omega$ ². Ennek megfelelően a ,,centrifugális potenciális energia'' -m $\omega$ ²x²/2, amihez hozzáadva a gravitációs helyzeti energiát a teljes potenciális energiára

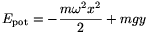
$E_{\rm pot}=-\frac{m\omega^2x^2}{2}+mgy$

adódik. A folyadék szabad felszínén a teljes potenciális energia mindenhol ugyanakkora kell legyen, ami a megadott parabola egyenletéhez vezet.

3. Az összefüggés levezetését a feladat nem kívánta meg. Mivel az Eötvös-versenyen bármilyen könyv használható a megoldáshoz, egyszerűen ki lehetett írni a megfelelő képletet például Budó: Kísérleti fizika, I. kötetének megfelelő fejezetéből.

Megvizsgálva a feladat konkrét adatait könnyen belátható, hogy a forgó folyadék felülete felveszi a forgásparaboloid alakot anélkül, hogy a folyadék széle a lombik nyakában egészen a gömbig felemelkedne. Felmerülhet azonban egy kérdés - és ez volt a kulcs a feladat helyes megoldásához -, hogy ha gondolatban meghosszabítanánk ezt a forgásparaboloidot egészen a gömbig, vajon nem ,,vágna-e bele'' a gömbbe? Mert ha igen, akkor ott a gömbben, a forgásparaboloid alatt is lehetne víz!

Vegyünk ismét egy, a forgástengelyen átmenő síkmetszetet! Határozzuk meg annak a parabolának a legmélyebb pontját, amely érinti a gömblombik síkmetszeteként adódó kört! Legyen ez a pont h-val mélyebben, mint a kör középpontja, ekkor a parabola egyenlete (a kör közepéhez választva a koordináta-rendszer kezdőpontját)

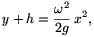
$y+h=\frac{\omega^2}{2g}\,x^2,$

a kör egyenlete pedig x²+y²=R². Ebből x²-et kifejezve és a parabola egyenletébe helyettesítve a kör és a parabola közös pontjainak y koordinátáira a következő másodfokú egyenletet kapjuk:

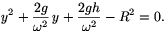
$y^2+\frac{2g}{\omega^2}\,y+\frac{2gh}{\omega^2}-R^2=0.$

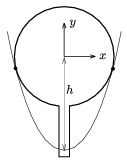
6. ábra

Amikor a parabola érinti a kört, a fenti egyenletnek csak 1 gyöke lehet, tehát a diszkrimináns zérus kell legyen, és éppen ez ad feltételt a h magasságra:

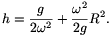
$h=\frac{g}{2\omega^2}+\frac{\omega^2}{2g}R^2.$

Behelyettesítve a g=9,81 m/s², $\omega$ =2 $\pi$ ^.3 s^-1, R=0,1 m adatokat, h-ra 0,195 m=19,5 cm adódik. A gömb sugara 10 cm, a nyak hossza ugyancsak 10 cm, együtt ez több, mint 19,5 cm.

A gömböt érintő paraboloid tehát a lefelé fordított lombik nyakának legalsó pontjánál fél centiméterrel feljebb halad! A feladat megoldásához tartozó paraboloid persze ennél az érintő paraboloidnál is valamivel feljebb halad, mégpedig úgy, hogy a gömblombik nyakában a paraboloid alatt maradó víz éppen annyival kevesebb az eredetileg ott volt víznél, amennyi a gömbben, egy körbefutó keskeny sávban a paraboloid alá került.

De hogyan került oda a víz? Voltak versenyzők, akik arra tippeltek, hogy a gömblombik felpörgetésekor talán odafreccsenhetett a víz. Ez a feltevés nincs híjával az iskolai szertárakban található forgatógépekkel szerzett érdekes tapasztalatoknak. Mégsem ez a probléma megoldása, hanem az, hogy a lombikban a cső nyakánál elpárolgó vízgőz egy része csapódik ki - megfelelő helyen - a lombik falára. Ennek a termodinamikai folyamatnak a hajtóereje pedig éppen az az ici-pici nyomáskülönbség, ami a lombikban fellép a nehézségi erő és a forgás együttes hatása miatt. Egy-egy forgásparaboloid mentén a víz a forgó koordináta-rendszerből nézve egyensúlyban van, hiszen éppen ez a feltétel határozza meg a felület alakját. Különböző forgásparaboloidokat összehasonlítva viszont a magasabban elhelyezkedő felület mentén nagyobb egy bizonyos vízmennyiség energiája, mint az alacsonyabban levő felületnél. Egyensúlyi állapotban a víz felszíne ugyanazon paraboloidon kell elhelyezkedjen a lombik nyakában és a gömbben is, ha nem így lenne, a párolgás és lecsapódás folyamata ,,megkeresné'' az alacsonyabb összenergiájú állapotot.

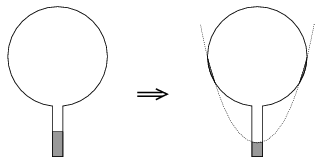
7. ábra

Végeredményben tehát a 7. ábrán látható vázlatos rajz (helyes indoklással) a feladat megoldása.

Megjegyzések. 1. A paraboloid helyzetének pontos meghatározása nem volt feladat - középiskolai matematikával ez nehéz is lett volna.

2. Béky Bence budapesti versenyző eljutott annak felismeréséhez, hogy lehet víz a lombik falán, de nem hitte el, hogy ez meg is valósulhat. ,,Ugyanúgy nem - írta -, mint ahogy egy, az asztalon álló pohár vízből sem mászik ki a víz az asztalra, hiába lenne ott kisebb az energiája.'' Nos, az érdekes az, hogy a víz onnan is kimászhat, még a tökéletes hőmérsékleti egyensúly esetén is, éppen a meglévő piciny barometrikus nyomáskülönbség miatt, ami a pohárban levő víz felszíne és az asztal (vagy még inkább a padló) szintje között fennáll. Letakarva egy üvegharanggal az asztalon álló pohár vizet, el is végezhető a kísérlet. Csak kissé soká kell várni! (Üvegharang nélkül is ,,kimászik'' a víz a pohárból, de a szoba nagy légtere miatt sehol sem csapódik le, hanem telítetlen gőz formájában a levegőben marad.)

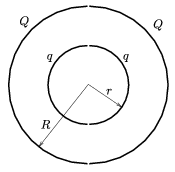
3. Két szigetelő félgömbhéjat (például két fél pingponglabdát) egymás közvetlen közelében helyezünk el a 8.a ábra szerint, koncentrikusan. Az egyikre Q, a másikra q töltést viszünk fel, egyenletesen.

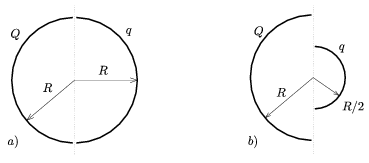
8. ábra

a) Mekkora erőt fejt ki egymásra e két test?

b) Megváltozik-e az eredmény, ha az egyik félgömbhéj csak fele akkora sugarú?

(Gagik Grigorjan [Örményország] feladata nyomán)

Megoldás. ,,Ha nem tudsz megoldani egy feladatot, csinálj belőle magadnak egy könnyebbet'' - tanácsolja Pólya György (1888-1985) ,,A gondolkodás iskolája'' c. könyvében. Tegyük ezt most mi is, mindaddig, amíg csak egy olyan feladatig jutunk, amit már meg tudunk oldani. Innen visszafejtve a gondolatsort, talán kaphatunk ötleteket a nehezebb feladatok megoldásához.

Foglalkozzunk először az a) kérdéssel! Mi lenne, ha mindkét félgömbhéjon ugyanakkora, (Q,Q) töltés lenne? Mi lenne, ha a töltések ellentétes előjelűek (Q,-Q) lennének? Ilyenkor jut az ember eszébe a síkkondenzátor.

A Q töltésű síkkondenzátor lemezein Q és -Q töltés, a lemezek között E térerősségű homogén tér van. A kondenzátor energiája

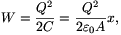
$W=\frac{Q^2}{2C}=\frac{Q^2}{2\varepsilon_0A}x,$

amiből látszik, hogy a lemezek közötti erő nagysága

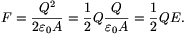
$F=\frac{Q^2}{2\varepsilon_0A}=\frac{1}{2}Q\frac{Q}{\varepsilon_0A} =\frac12QE.$

Innen lépegessünk visszafelé! Ha nem Q és -Q, hanem Q és +Q töltés van a lemezeken, akkor annyi a különbség, hogy nem vonzó, hanem taszító erő lép fel, E pedig annak a térerősségnek a nagysága, ami a lemezeken kívül jelenik meg.

Két szembefordított, Q töltéssel egyenletesen feltöltött gömbhéj elektromos tere ugyanaz, mint ami egyetlen gömbön kívül lép fel, ha az 2Q töltéssel van egyenletesen feltöltve. Ekkor a térerősség a gömbön kívül akkora, amekkora a 2Q nagyságú, a gömb közepén elhelyezett ponttöltéstől jönne létre:

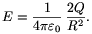
$E=\frac1{4\pi\varepsilon_0}\,\frac{2Q}{R^2}.$

A gömb felületén a töltéssűrűség:

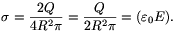
$\sigma=\frac{2Q}{4R^2\pi}=\frac{Q}{2R^2\pi}= (\varepsilon_0E).$

Ugyanitt az energiasűrűség (egységnyi térfogatra jutó energia, nyomás jellegű mennyiség):

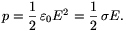
$p=\frac12\,\varepsilon_0E^2=\frac12\,\sigma E.$

Egy elektromosan töltött felület adott nagyságú darabkájára ható erőt a felület nagysága, töltéssűrűsége és a felület közvetlen közelében mérhető elektromos térerősség egyértelműen meghatározza. Ez az elektrosztatikus ,,nyomás'' tehát nemcsak a síkkondenzátor, hanem a töltött félgömbhéj esetében is a fentebb kiszámított p-vel (az energiasűrűséggel) egyezik meg.

A félgömbhéjra ható eredő erő ugyanakkora, mint a félgömbhéjat gondolatban lezáró körlapra ható erő lenne p nyomás esetén (hiszen egy p nyomású gázba helyezett lezárt félgömbre a gáz által kifejtett eredő erő nyilván zérus). A kérdéses erő tehát

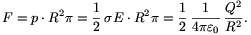
$F=p\cdot R^2\pi=\frac12\,\sigma E\cdot R^2\pi=\frac12\,\frac1{4\pi\varepsilon_0}\,\frac{Q^2}{R^2}.$

Kiszámítottuk a két szembefordított, egyenként Q töltésű félgömbhéj között fellépő erőt. Térjünk vissza most az eredeti a) kérdéshez, ami az eddig tárgyalt esettől csak abban tér el, hogy az egyik félgömbhéjon nem Q, hanem q töltés van! Az elektrosztatikus erő arányos a test töltésével, ezért

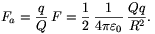
$F_a=\frac{q}{Q}\,F= \frac12\,\frac1{4\pi\varepsilon_0}\,\frac{Qq}{R^2}.$

Megjegyzés. Látható, hogy a Coulomb-törvényhez nagyon hasonló formulát kaptunk, csupán a képletben szereplő numerikus együttható tér el az ismert kifejezésétől. Akár meg is kereshetnénk azokat a pontokat a félgömbök belsejében, ahova elhelyezett Q illetve q ponttöltések éppen ekkora erőt fejtenek ki egymásra; ez azonban nem volt kérdés a feladatban. Megjegyezzük, hogy a kérdéses pontok nem esnek egybe a homogén tömegeloszlású félgömbhéjak tömegközéppontjaival, mint azt több versenyző tévesen állította. Az eltérésnek az az oka, hogy csak a homogén gravitációs erőtér hatása helyettesíthető a tömegközéppontba képzelt testre ható erővel, a Coulomb-féle erőtér pedig inhomogén!

A b) kérdés megoldásához ismét idézzük fel Pólya György tanácsát! A kérdéses aszimmetrikus elrendezés helyett tekintsünk egy szimmetrikusat, amit feltehetőleg egyszerűbb lesz kezelnünk. Egészítsük ki a b) elrendezést a ,,tükörképével'' (9. ábra)! Írjuk fel a bal oldali két félgömbhéj által a jobb oldali két félgömbhéjra kifejtett eredő erőt! Ez négy erőből tehető össze:

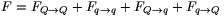
$F=F_{Q\to Q}+F_{q\to q}+F_{Q\to q}+F_{q\to Q}$

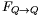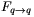Az összeg két utolsó tagja egyenlő egymással, és mindegyikük éppen az az F_b erő, amit keresünk! Ha tehát ki tudjuk számítani F-et, akkor $F_{Q\to Q}$ és $F_{q\to q}$ ismeretében (amelyeket az a) kérdésre tudunk visszavezetni) a keresett erő meghatározható.

9. ábra

F kiszámításához tekintsük azt az elektromos teret, amit két koncentrikus gömbhéj hoz létre: a belső, r sugarú, 2q töltésű gömbhéj és a külső, R sugarú, 2Q töltésű gömbhéj. Gyakorlatilag ez lesz a négy félgömnhéj által létrehozott elektromos tér is.

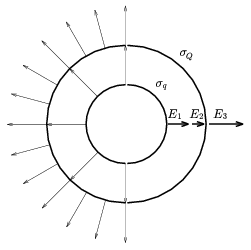
10. ábra

A kis gömbhéj belsejében az elektromos térerősség nulla. E gömb felületén a töltéssűrűség:

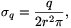
$\sigma_q=\frac{q}{2r^2\pi},$

a térerősség pedig a gömb felületénél, de kívül:

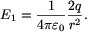
$E_1=\frac{1}{4\pi\varepsilon_0}\frac{2q}{r^2}.$

Ennek a kis gömbnek a tere a nagy gömb felületénél, annak belsejében:

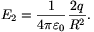
$E_2=\frac{1}{4\pi\varepsilon_0}\frac{2q}{R^2}.$

A nagy gömb felületén a töltéssűrűség:

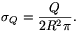
$\sigma_Q=\frac{Q}{2R^2\pi}.$

A nagy gömbön kívüli térrészben a térerősségért mindkét gömb töltése felelős. Az elektromos térerősség nagysága

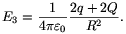
$E_3=\frac{1}{4\pi\varepsilon_0}\frac{2q+2Q}{R^2}.$

A fenti kifejezések segítségével - az a) kérdésnél alkalmazott gondolatmenetet követve - F-et a következő módon számíthatjuk ki:

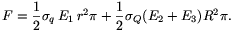
$F=\frac12\sigma_q\,E_1\,r^2\pi+ \frac12\sigma_Q(E_2+E_3)R^2\pi.$

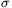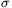Behelyettesítve $\sigma$ _q, $\sigma$ _Q, E₁, E₂ és E₃ fenti kifejezéseit, F meghatározható.

Az a) kérdésre adott választ felhasználva

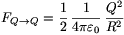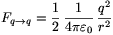$F_{Q\to Q}=\frac12\,\frac1{4\pi\varepsilon_0}\,\frac{Q^2}{R^2}$ és $F_{q\to q}= \frac12\,\frac1{4\pi\varepsilon_0}\,\frac{q^2}{r^2}$ .

Ezek után a keresett 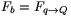$F_b=F_{q\to Q}$ -ra kapjuk:

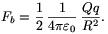
$F_b=\frac12\,\frac1{4\pi\varepsilon_0}\,\frac{Qq}{R^2}.$

Az eredmény meglepő, hiszen független r-től, így a b) esetben is ugyanakkora az erő, mint az a) esetben! (Ennyi számolás után meg is érdemeltünk egy kellemes meglepetést.)

Megjegyzés. A b) kérdést megválaszoló versenyzők több kiváló ötlettel is éltek. Nagy Márton (Budapest) gondolatban körülvette a 11.a ábrán látható elrendezést (amelyen az egyszerűség kedvéért csak a kisebb félgömbhéjra ható erőt tüntettük fel) egy R-nél ,,hajszálnyival'' nagyobb sugarú, -2Q töltésű gömbhéjjal (11.b ábra). Így a félgömbhéjak között ható erőt nem változtatta meg, hiszen az egyenletesen töltött gömbhéj térerőssége belül nulla. Ez az elrendezés nyilván egyenértékű a 11.c ábrán láthatóval, amiből -Q előjelét megváltoztatva a 11.d ábrán feltüntetetthez jutunk. Tükrözzük ezt az elrendezést a félgömbhéjak képzeletbeli határsíkjára (11.e ábra). Azt kaptuk, hogy a Q töltésű (egyenletes töltésű) félgömbhéj ugyanakkora erőt fejt ki egy ,,benne lévő'' másik, q töltésű félgömbhéjra, mint amekkorát egy ,,belőle kilógó'' q töltésű félgömbhéjra. Ezek szerint egy 2q töltésű gömbre a nagy félgömbhéj 2F erőt fejtene ki, q össztöltésű gömbre pedig ennek felét, F-et (11.f ábra).

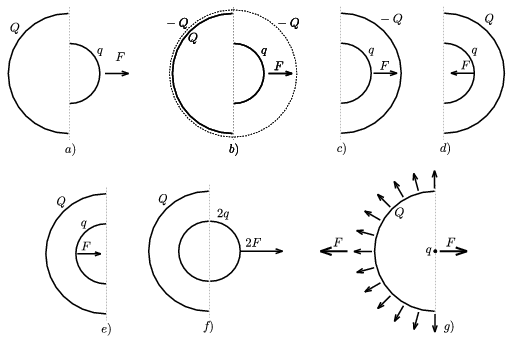
11. ábra

Most már csak a hatás-ellenhatás törvényét kell alkalmaznunk: a q töltésű gömb (amelynek elektromos tere a gömbön kívül egy ponttöltés terével is helyettesíthető, tehát nem függ r-től!) a Q töltésű félgömbhéjra éppen a keresett F nagyságú erőt fejti ki (11.g ábra). A végeredmény a Coulomb-törvény és a gáznyomásos hasonlat alkalmazásával adódik:

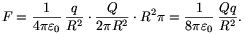
$F=\frac1{4\pi\varepsilon_0}\,\frac{q}{R^2}\cdot\frac{Q}{2\pi R^2}\cdot R^2\pi=\frac1{8\pi\varepsilon_0}\,\frac{Qq}{R^2}.$

Még tovább ment a feladat általánosításában Csóka Endre (Debrecen), aki - a fentiekhez hasonló ,,tükrözéses módszerrel'' - megmutatta, hogy a félgömbhéjak között ható F erő nagysága akkor is a fent kiszámított érték, ha a két félgömb szimmetriatengelye tetszőleges $\alpha$ szöget zár be egymással. Az erő nagysága a töltések szorzatán kívül csak a nagyobb félgömbhéj sugarától függ, iránya pedig a nagyobb félgömb szimmetriatengelyével párhuzamos, jóllehet a hatásvonala általában nem megy át a félgömbhéjak közös középpontján (12.a ábra). Ez az eredmény is meglepő, hiszen ha r és R majdnem egyforma nagyságúak, egyikük csupán egy parányival nagyobb a másiknál, akkor az erő iránya ugrásszerűen változik, attól függően, hogy melyik sugár is a nagyobb (12.b és 12.c ábrák).

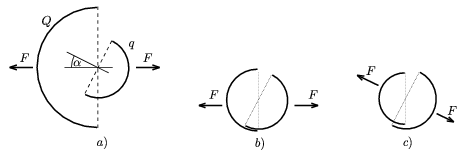
12. ábra

Az ünnepélyes eredményhirdetésre és díjkiosztásra 2002. november 29-én került sor az ELTE TTK lágymányosi (északi) épületének 0.83-as tantermében. Itt a Versenybizottság elnöke először megemlékezett a 100 évvel ezelőtti Eötvös-verseny akkori nyerteséről, Kőnig Dénes (1884-1944) matematikusról, majd bemutatta a hallgatóságnak Zanati Tibort, aki 50 évvel ezelőtt nyert díjat az Eötvös-versenyen. Ezután ismertette a feladatok helyes megoldását, majd felkérte Gyulai József akadémikust, az Eötvös Loránd Fizikai Társulat elnökét, hogy adja át a díjakat.

A Versenybizottság (Radnai Gyula elnök, Károlyházy Frigyes és Gnädig Péter) döntése alapján

I. díjat nyert és 15 ezer Ft jutalmat kapott Nagy Márton, az ELTE fizikus hallgatója, aki a budapesti Piarista Gimnáziumban érettségizett, mint Futó Béla tanítványa.

II. díjat nyert és 10-10 ezer Ft jutalmat kapott Béky Bence, a BMGE mérnök-fizikus hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Horváth Gábor tanítványa, valamint Tóth Sándor, a csongrádi Batsányi János Gimnázium 12. évf. tanulója, Szucsán András és Hilbert Margit tanítványa.

III. díjat nyert és 5-5 ezer Ft jutalmat kapott Csóka Endre, a debreceni Fazekas Mihály Gimnázium 12. évf. tanulója, Kiszely Ildikó és Szegedi Ervin tanítványa, Siroki László, a BMGE műszaki informatikus hallgatója, aki a debreceni Fazekas Mihály Gimnáziumban érettségizett mint Simon Gyula és Szegedi Ervin tanítványa; Szabó Áron, a debreceni Fazekas Mihály Gimnázium 11. évf. tanulója, Simon Gyula és Szegedi Ervin tanítványa, továbbá Vehovszky Balázs, a budapesti Piarista Gimnázium 12. évf. tanulója, Futó Béla tanítványa.

Kiemelt dicséretet kapott Balogh László, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évf. tanulója, Horváth Gábor tanítványa.

Dicséretet kaptak a következők: Geresdi Attila, a BMGE mérnök-fizikus hallgatója, aki a pécsi Árpád fejedelem Gimnáziumban érettségizett Kotek László tanítványaként, Hamar Gergő, az ELTE fizikus hallgatója, aki a dombóvár Illyés Gyula Gimnáziumban érettségizett mint Freller Miklós tanítványa, Pápai Tivadar, a BMGE műszaki informatikus hallgatója, aki a barcsi Dráva Völgye Középiskolában érettségizett mint Horváth Ferenc és Kotek László tanítványa, valamint Rácz Béla András, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. évf. tanulója, Horváth Gábor tanítványa.

Idén első alkalommal vehette át a verseny I. díjasa a Társulat Eötvös-verseny érmét.

A verseny valamennyi díjazott és dicséretben részesült versenyzője a Nemzeti Tankönyvkiadótól 4-4 ezer forintos könyvutalványt kapott, az ünnepélyes díjkiosztáson megjelent tanáraik pedig a Műszaki Kiadó, a Nemzeti Tankönyvkiadó és a Typotex Kiadó ajándékkönyveiből válogathattak.

A program befejeztével a még ott maradt tanárok és diákok kihasználhatták az alkalmat, hogy egymással s a korábbi Eötvös-versenyek jelenlevő nyerteseivel elbeszélgessenek, s újra megtekintsék a ,,Csollány-feladathoz'' kapcsolódó demonstrációs kísérleteket.

A díjazott és dicséretet nyert versenyzők: Első sor (balról jobbra): Nagy Márton és Tóth Sándor Középső sor: Csóka Endre, Siroki László, Szabó Áron és Vehovszky Balázs Felső sor: Geresdi Attila, Pápai Tivadar, Hamar Gergő, Balogh László és Rácz Béla András
Zanati Tibor, az 1952. évi Eötvös-verseny díjazottja	Nagy Márton, a 2002. évi I. díjas az Eötvös-éremmel

Radnai Gyula

Már regisztráltál?
Új vendég vagy?