New exercises and problems in Mathematics
September 1999
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in September 1999 |
C. 545. A tube contains 75 ml of toothpaste. Determine, in metres, the length of the toothpaste one could squeeze out of the tube, given that the circular cross section of the paste leaving the tube has a diameter of 6 mm.
C. 546. The integers from 1 to 1999 are written side by side in a row. Determine the 1999th digit in the row.
C. 547. Which point of the graph of the equation y(x2+y2)-x(x2+y2)-y+x=0 is closest to the point P having coordinates (3,4)?
Proposer: Bánhegyi László, Budapest
C. 548. The minute hand, the hour hand, and the second hand of a clock are fixed to the same axis. They cover each other at 12 o'clock. Find the next time the three hands cover each other.
C. 549. Given a cube ABCDEFGH of unit edge, consider the point that trisects segment BE closer to E (see the figure). How far is this point from the plane passing through points C,F and H (See Figure)?
Proposer: Bánhegyi László, Budapest
 |
New problems in September 1999 |
B. 3292. The kitchen floor has to be renovated and the
two children in the family may choose the pattern of the ceramic
tiles. One of them prefers the pattern shown on the left side, while
the other child prefers the one shown on the right side. In the end,
they decide to choose the pattern with the more brown colour. Which
one is it?
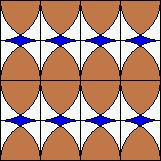
B. 3293. The positive integers a and b satisfy 34a=43b. Prove that a+b is a composite number.
Proposer: Róka Sándor, Nyíregyháza
B. 3294. The numbers 1, 2, 3, ..., 20 are written on a board. We may erase any two numbers a and b and replace them by ab+a+b. After repeating this procedure altogether 19 times, what number may remain on the board in the end?
Proposer: Róka Sándor, Nyíregyháza
B. 3295. In a triangle, determine those lines incident to the centroid which halve the area of the triangle.
Proposer: Bogdán Zoltán, Cegléd
B. 3296. A locust, a grasshopper and a cricket are sitting in a long, straight ditch, with the locust on the left and the cricket on the right side of the grasshopper. From time to time one of them leaps over one of its neighbours in the ditch. Is it possible that they will be sitting in their original order in the ditch after 1999 jumps will have occurred?
Proposer: Róka Sándor, Nyíregyháza
B. 3297. In a right triangle with legs a,b and
hypotenuse c, prove that 
.
Proposer: Paulovics Illés
B. 3298. Each lateral edge of a triangular pyramid is of unit length, moreover, they form angles of 60o, 90o and 120o, respectively. Calculate the volume of the pyramid.
Proposer: Vajda Szilárd, Kolozsvár
B. 3299. There are n coins, each of radius r, placed on a round table of radius R such a way that each coin has a side which wholly touches the surface of the table. On the other hand, no more coin can be placed on the table. Prove that 
.
Proposer: Róka Sándor, Nyíregyháza
B. 3300. In a convex polytope, the vertices of one face are coloured with red while the remaining vertices are coloured with blue. Prove that the polytope has either a blue vertex whose valence is at most 5 or a red vertex of valence 3. (The valence of a vertex is the number of edges starting at it.)
B. 3301. A set H has |H|=n elements. Prove that
.
Proposer: Róka Sándor, Nyíregyháza
 |
New advanced problems in September 1999 |
A. 215. Points P,Q and R lie on the
ellipsoid of equation 
such that
segments OP, OQ, OR are pairwise perpendicular, where O
denotes the centre of the ellipsoid. Prove that the distance of plane
PQR from O is independent of the position of the points
P, Q, R.
Yugoslawian competition problem
A. 216. Prove that, for any positive integer n, there exists a polynomial p of degree at most n whose coefficients are all integers such that, p(x) is divisible by 2n for every even integer x, and p(x)-1 is divisible by 2n for every odd integer x.
Proposer: Hajnal Péter, Szeged
A. 217. The positive integers a1, a2, ..., an have 1 as their highest common factor. Any two of them, moreover, have the same least common multiple. Prove that there exists an integer p such that, for any integer u, exactly one of the numbers u and p-u can be expressed in the form a1x1+a2x2+...+anxn with a suitable choice of nonnegative integers x1, x2, ..., xn.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.