Az 1999. októberi számban kitűzött A-jelű matematika feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 218. Határozzuk meg azokat a folytonos 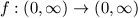függvényeket, amelyekre tetszőleges x, y pozitív számok esetén

.

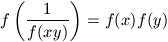Megoldásvázlat. A függvényegyenletet átírva a g(x)=log f(e^-x) függvényre,

g(g(x+y))=g(x)+g(y).   (1)

Ezt felírva a 0 és x+y számokra is,

g(x)+g(y)=g(g(x+y))=g(g(0+(x+y)))=g(0)+g(x+y).   (2)

Bevezetve a h(x)=g(x)-g(0) függvényt, (2) a h(x+y)=h(x)+h(y) alakba írható. A h függvény folytonos és additív, tehát h(x)=ax egy alkalmas a valós számmal. A g(0)=b jelöléssel g(x)=ax+b. Ezt visszahelyettesítve (1)-be

(a²-a)(x+y)+(a-1)b=0,   (3)

ami kétféleképpen lehetséges: a=1 és b akármi, vagy a=b=0. Az (1) egyenletnek ezek a megoldásai.

A megoldásokat visszaírva f-be, az első esetben

a második esetben

f(x)=1.

A függvényegyenletnek tehát a konstans 1 és a c/x alakú (c>0) függvények tesznel eleget.

Megjegyzés.

A megoldás hasonlóan megy akkor is, ha nem kötjük ki a folytonosságot, csak a h additív függvényt nem lehet olyan egyszerűen felírni. A (3) egyenlet helyett azt kapjuk, hogy tetszőleges x-re

h(h(x))-h(x)=b-h(b).   (4)

Az x=0 helyettesítésből h(b)=b, és h(h(x))=h(x), azaz h egy projekció. Könnyű ellenőrizni, hogy ez a két feltétel elégséges is, azaz (1) megoldásai a g(x)=h(x+c) alakú függvények, ahol h tetszőleges projekció.

A. 219. A H ponthalmaz a sík 2n pontját tartalmazza, közülük semelyik három nem esik egy egyenesre. Ha P és Q két különböző H-beli pont, és H-nak pontosan ugyanannyi pontja esik a PQ egyenes két oldalára, akkor a PQ szakaszt felező szakasznak hívjuk. Bizonyítsuk be, hogy ha a felező szakaszok száma n, akkor közülük bármelyik kettő metszi egymást.

Javasolta: Solymosi József, Budapest

Megoldásvázlat. Ha bármelyik ponton át fektetve és körbeforgatva egy egyenest, az egyenes két oldalán levő pontok számának különbsége mindig 1-gyel változik, és 180 fok elfordulás után az előjelet vált. Ebből következik, hogy minden pontból indul ki felező szakasz. A felező szakaszok száma ezért pontosan akkor n, ha mindegyik pontból pontosan egy felező szakasz indul ki.

Tegyük fel, hogy van két felező szakasz, ami nem metszi egymást. Könnyű meggondolni, hogy a két felező szakasz nem lehet párhuzamos. (A párhuzamosságot a pontok kis elmozdításával is elkerülhenénk.) Az egyik felező szakasz egyenese - jelöljük e-vel - a másik szakasz - legyen AB - mondjuk A-n túli meghosszabbítását metszi.

Húzzunk párhuzamost e-vel A-n keresztül, legyen ez e', Az AB=f egyenest A körül egy nagyon kis szöggel elforgatva pozitív és negatív irányba, az így kapott f₁ és f₂ egyenesek két oldalán ugyanazok a pontok helyezkednek el, mint f két oldalán, kivéve a B pontot. Ezért f₁-nek és f₂-nek a B-t tartalmazó oldalán eggyel több pont van, mint a másikon.

Ugyanakkor az e' egyenesnek a B-t tartalmazó oldalán kevesebb pont van, mint a másikon, mert e egy felező, amelynek B-tartalmazó partján van a A pont, a vele párhuzamos e' egyenesnek viszont az A pont nincs a B-t tartalmazó partján, ezen kívül e'-nek a B-t nem tartalmazó oldalán van az e egyenes két pontja is.

Körbeforgatva az f egyenest A körül, az f₁ és e' illetve f₂ és e' egyenesek között is kell lennie felező szakasznak. Az A pontból tehát legalább három felező szakasz indul ki.

A. 220. Jelöljük tetszőleges pozitív egész n számra S(n)-nel az n jegyeinek összegét tízes számrendszerben. Igazoljuk, hogy

.

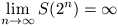Megoldásvázlat. Legyen k rögzített pozitív egész. Tetszőleges n-re jelölje 2ⁿ 10-es számrendszerbeli felírásában c_n az utolsó k számjegy által alkotott egészt, b_n az előtte levő 3k jegy által alkotott számot, végül a_n az összes ezek előtt álló számjegyből alkotott számot.

2ⁿ=10^4ka_n+10^kb_n+c_n,

ahol 0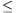b_n<10^3k és 0<c_n<10^k. (A c_n nem lehet 0, mert például 2ⁿ utolsó jegye sem 0.)

A 10^kb_n+c_n=2ⁿ-10^4ka_n szám osztható 2^4k-nal, a c_n szám viszont nem, mert 0<cⁿ<10^k<2^4k. Emiatt b_n nem lehet 0.

Legyen most n>4^m+1, és tekintsük 2ⁿ utolsó 4^m jegyét. Az előbbi meggondolást k=4⁰, 4¹, ..., 4^m-1-nre megismételve ki tudunk jelölni összesen m darab olyan páronként diszjunkt számjegyhalmazt, amelyek mindegyikében szerepel legalább egy 0-tól különböző számjegy. Ezért n>4^m+1 esetén S(2ⁿ)m.