Az 1999. novemberi A-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 221. Legyenek az N négyzet csúcsai a (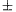 1999;
1999; 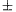 1999) koordinátájú pontok, a H háromszög
csúcsai pedig (-1; 0), (0; -1) és (1; 1). A H
háromszögnek legfeljebb hány egymásba nem nyúló, eltolt példányát
lehet elhelyezni az N négyzetben?
1999) koordinátájú pontok, a H háromszög
csúcsai pedig (-1; 0), (0; -1) és (1; 1). A H
háromszögnek legfeljebb hány egymásba nem nyúló, eltolt példányát
lehet elhelyezni az N négyzetben?
Javasolta: Pap Gyula, Debrecen
Megoldásvázlat. Legyen T az a hatszög, amelynek csúcsai
(- ; -1), (
; -1), ( ;
;  ), (1;
), (1;  ), (
), ( ; 1), (-
; 1), (- ;
;  ),
(-1; -
),
(-1; - ). Ellenőrizhető,
hogy H két eltolt példánya pontosan akkor nem nyúlik egymásba,
ha a T ugyanolyan vektorokkal eltolt példányai nem nyúlnak
egymásba, valamint H egy eltolt példánya akkor van az N
négyzetben, ha T ugyanolyan vektorral eltolt példánya is abban
helyezkedik el. A végeredmény tehát nem változik, ha H helyett
T-vel oldjuk meg a feladatot.
). Ellenőrizhető,
hogy H két eltolt példánya pontosan akkor nem nyúlik egymásba,
ha a T ugyanolyan vektorokkal eltolt példányai nem nyúlnak
egymásba, valamint H egy eltolt példánya akkor van az N
négyzetben, ha T ugyanolyan vektorral eltolt példánya is abban
helyezkedik el. A végeredmény tehát nem változik, ha H helyett
T-vel oldjuk meg a feladatot.

Bebizonyítjuk, hogy a T hatszög illetve a H háromszög eltolt példányaiból az ábrán látható módon helyezhető el a legtöbb, összesen 26652=7102225 darab.


A hatszög példányai hézag nélkül lefedik a négyzet középső részét, mindössze azt kell igazolnunk, hogy N határai mentén nem maradhat ki kisebb terület.
Az alábbi ábrán mindegyik sarokban pirossal megjelöltük azokat a
pontokat amelyeket T egy eltolt példánya sem tartalmazhat. Az
N további oldalszakaszai mentén fennmaradó terület egy részét
felbonthatjuk olyan háromszögekre és trapézokra (az ábrán kék színnel
jelöltük), amelyek alapjai merőlegesek N oldalaira, egyik
alapjuk legalább  , magasságaik
összege pedig kiadja N-nek a pirosra színezett sarkok elhagyása
után fennmaradó oldalszakaszait.
, magasságaik
összege pedig kiadja N-nek a pirosra színezett sarkok elhagyása
után fennmaradó oldalszakaszait.

A háromszögek és trapézok területének összege a második ábrán látható elrendezésben minimális.
A. 222. Az a, b, c egész számok legnagyobb közös osztója 1. Az (a, b, c) számhármast más számhármasokra cserélhetjük úgy, hogy minden lépésben az egyik számot növeljük vagy csökkentjük a számhármas egy másik elemének valamilyen többszörösével. Igaz-e, hogy az a, b, c számok megválasztásától függetlenül, legfeljebb 10 lépésben eljuthatunk az (1, 0, 0) számhármashoz?
Javasolta: Abért Miklós, Budapest
Megoldásvázlat. Megmutatjuk, hogy legfeljebb 5 lépésben mindig eljuthatunk az (1, 0, 0) számhármashoz.
Először bebizonyítjuk, hogy ha b nem 0, akkor
létezik olyan k egész szám, amelyre b és
c+ka relatív prímek. Legyen b prímtényezős
felbontása  . A k számot
k=k1+k2p1+k3p1p2+...+knp1p2...pn-1 alakban fogjuk felírni alkalmas
k1, ..., kn egész számokkal.
. A k számot
k=k1+k2p1+k3p1p2+...+knp1p2...pn-1 alakban fogjuk felírni alkalmas
k1, ..., kn egész számokkal.
Azt, hogy c+ka osztható-e p1-gyel, k1 határozza meg. Mivel a és c közül legalább az egyik nem osztható p1-gyel, k1-et meg tudjuk úgy választani, hogy c+ka se legyen osztható p1-gyel. A k1 megválasztása után k2-t választjuk meg úgy, hogy c+ka ne legyen osztható p2-vel, ... végül kn-et választjuk meg úgy, hogy c+ka ne legyen osztható pn-nel. Ezzel egy olyan k számot konstruáltunk, amelyre c+ka nem osztható b egyik prímosztójával sem.
(Ezt a segédtételt a Dirichlet-tétel felhasználásával is be lehetett volna bizonyítani. Ha a és c egyike sem 0, a legnagyobb közös osztójuk d, akkor létezik olyan k egész és p>b prímszám, amelyre c+ka=pd.)
Most megmutatjuk, hogyan lehet legfeljebb 5 lépésben eljutni az (1, 0, 0) számhármashoz. Első lépésben egy olyan (a1, b1, c1) számhármast állítunk elő, amelyben b1 és c1 relatív prímek. Ha b nem 0, akkor a segédtétel alapján ez lehetséges. Ha b=0, akkor a és c relatív prímek, ezért az ugyancsak egy lépésben előállítható (a, a, c) számhármas megfelelő.
Mivel b1 és c1 relatív prímek, léteznek olyan x és y egész számok, amelyekre a+xb1+yc1=1. Ebből következik, hogy a (a1, b1, c1) számhármasból két lépésben eljuthatunk az (1, b1, c1) számhármashoz. Ebből pedig két triviális lépésben a kívánt (1, 0, 0) számhármashoz.
Megjegyzés. Számhármasok helyett számpárokkal az állítás nem igaz.
A. 223. Keressük meg az összes olyan f:R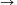 R függvényt, amelyre
R függvényt, amelyre
(1) f(x-f(y))=f(x+y1999)+f(f(y)+y1999)+1
teljesül tetszőleges x, y valós számok esetén.
Megoldásvázlat. Az x helyére f(y)-t írva kapjuk, hogy
f(f(y)+y1999)=(f(0)-1)/2.
Ezt visszaírva (1)-be, x helyére (x+f(y))-t helyettesítve
(2) f(x)=f(x+f(y)+y1999)+(f(0)+1)/2.
Legyen g(x)=f(x)+x1999 és c=(f(0)+1)/2; ezeket beírva (2)-be,
(3) f(x)=f(x+g(y))+c.
Az (1) azonosságból, x=y=0 helyettesítéssel látható, hogy f(0)=g(0) nem lehet 0.
Legyen h(y)=g(y+g(0))-g(y). A (3) azonosságból következik, hogy
(4) f(x+h(y))=f(x+h(y)+g(y))+c=
=f(x+g(y+g(0)))+c=f(x).
Kifejtve h definícióját,
h(y)=g(y+g(0))-g(y)=
=(y+g(0))1999-y1999+f(y+g(0))-f(y)=
=(1998g(0)y1998+...+g(0)1999)-c,
ami y-nak egy 1998-adfokú polinomja. Mivel a h polinom értékkészlete egy félegyenes, a (4) azonosságból következik, hogy az f függvény konstans, az (1) függvényegyenlet alapján értéke csak -1 lehet.
Az egyetlen megoldás a konstans -1 függvény.

