Az 1999. novemberi B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3312. Szilveszter észrevette, hogy ha születési évének számjegyeit összeadja, azt a számot kapja, amely nagyapja születési évszámának utolsó két jegyéből áll. Szilveszter születési évszámának utolsó két jegye összeolvasva pedig nagyapja jelenlegi életkora. Hány éves Szilveszter? (3 pont)
Javasolta: Nyul Balázs 9. o. t., Debrecen
Megoldásvázlat. Szilveszter nagyapjának életkora kétjegyű, ezért a feladatban szereplő évszámok mind az 1900-as évekből valók.
Legyen Szilveszter születési éve 19ab=1900+10a+b. A feltételekből tudjuk, hogy nagyapja születési éve 1900+(1+9+a+b), életkora pedig 10a+b. E két információból
(1910+a+b)+(10a+b)=1999, vagyis 11a+2b=89.
Ennek az egyenletnek a 0, 1, ..., 9 számjegyek között egy megoldása van: a=7, b=6. Tehát Szilveszter 1976-ban született, nagyapja 1923-ban, Szilveszter 23 éves.
B. 3313. Az ABCD rombuszt a BD átlója két
szabályos háromszögre vágja. Az AD szakaszon adott egy P,
a CD szakaszon pedig egy Q pont úgy, hogy a
PBQ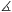
=60o. Mekkora a PBQ háromszög másik két
szöge? (3 pont)
Megoldásvázlat.
A B körüli 60o-os elforgatás a CD szakaszt és a a BQ félegyenest a DA szakaszba illetve a BP félegyenesbe viszi, az előbbi kettő metszéspontját, Q-t az utóbbi kettő metszéspontjába, P-be. Ezért a PBQ háromszög szabályos.
B. 3314. Meg lehet-e számozni egy szabályos oktaéder éleit az 1, 2, ..., 12 számokkal úgy, hogy mindegyik csúcsban ugyanannyi legyen az oda befutó élekre írt számok összege? (3 pont)
Javasolta: Reményi Gusztáv, Budapest
Megoldásvázlat. Egy lehetséges számozás látható az ábrán.
B. 3315. Adjuk meg azt az f(x)=ax alakú függvényt, amely a g(x)=x2 függvényt "jól" közelíti az x=0,1; 0,2; ...;0,5 helyeken abban az értelemben, hogy az ezeken a helyeken számított |f(x)-g(x)| hibák közül a legnagyobbik a lehető legkisebb. (4 pont)
Javasolta: Bakonyi Gábor, Budapest
Megoldásvázlat. A hibák rendre |0,1a-0,01|, |0,2a-0,04|, |0,3a-0,09|, |0,4a-0,16|, |0,5a-0,25|. Ezeket ábrázoltuk az alábbi ábrán:
A hibák maximuma (az ábrán sárga vonallal jeleztük)
| 0,25-0,5a | ha a  ; | |
| 0,2a-0,04 | ha
a0,5; | |
| 0,3a-0,09 | ha 0,5a0,7; | |
| 0,4a-0,16 | ha 0,7a0,9; | |
| 0,5a-0,25 | ha 0,9a. |
A maximumok minimuma a=-nél van, értéke 
.
B. 3316. Legyen P az ABC háromszög egy belső pontja. Az AP és a BP egyenesek messék a háromszög szemközti oldalát a D illetve az E pontban. Mutassuk meg, hogy ha AP=BP és BE=CE, akkor 1/AP=1/AD+1/AC. (4 pont)
Javasolta: Lee, Ho-joo, Korea
Megoldásvázlat.
Írjuk fel Menelaosz tételét az AEP háromszögre és a BDC egyenesre:
.
Egyszerűsítsünk BE=CE-vel, és írjunk BP helyett AP-t:
Ez, átrendezve, éppen a feladat állítása.
B. 3317. Oldjuk meg a következő egyenletet:
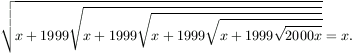
(4 pont)
Javasolta: Hans Zoltán, Nagykanizsa
Megoldásvázlat. Behelyettesítéssel könnyen ellenőrizhető, hogy x=0 és x=2000 megoldások. Megmutatjuk, hogy más megoldás nincs.
Ha 0<x<2000, akkor 
, és
Ha x>2000, akkor az összes egyenlőtlenség fordítva áll.
B. 3318. Az egységnyi sugarú k1 és k2 körök a P pontban érintik egymást. A két kör egyik P-n át nem menő közös érintője az e egyenes. Legyen i>2 esetén ki az a ki-2-től különböző kör, amely érinti k1-et, ki-1-et és e-t. Határozzuk meg k1999 sugarát. (5 pont)
Megoldásvázlat.
Jelöljük kn középpontját On-nel, sugarát Rn-nel, e-vel való érintési pontját Tn-nel.
Az O1T1TnOn, O1T1Tn+1On+1, On+1Tn+1TnOn derékszögű trapézokból
,
és
,
amiből
és
Mivel R2=1, ebből következik, hogy n>1 esetén
és
speciálisan
B. 3319. Ismert, hogy egy adott körbe írható négy csúcsú síkidomok közül a négyzet területe a legnagyobb. Igaz-e, hogy egy adott gömbbe írható nyolc csúcsú testek közül a beírható kocka térfogata a legnagyobb? (4 pont)
Megoldásvázlat. Nem a kocka térfogata a legnagyobb.
Az r sugarú gömbbe írt kocka térfogata 
, ezzel szemben az ugyanakkora gömbbe írt szabályos
hatszög alapú kettős gúla térfogata 
. (A gömbbe írt nyolc csúcsú testek közül ennek a
legnagyobb a térfogata.)
B. 3320. Oldjuk meg a következő egyenletet:
xx1/2=1/2.
(5 pont)
Javasolta: Lovrics László, Budapest
Megoldásvázlat. Legyen x=y2. Ezt behelyettesítve az egyenletbe
y2y=1/2.
Deriválással ellenőrizhető, hogy az y2y függvény 0<y1/e esetén szigorúan monoton fogy, 1/ey esetén szigorúan monoton nő,
ezért mindkét intervallumban legfeljebb egyszer-egyszer veszi fel az
1/2-et. Behelyettesítéssel ellenőrizhető, hogy ez a két hely az 1/2 és
az 1/4. Ehhez a két y értékhez tartozó megoldások:
x1=1/4 és x2=1/16.
B. 3321. Legyen K egy konvex sokszög. Mutassuk meg, hogy elhelyezhető a síkon 6 darab K-val egybevágó sokszög úgy, hogy ezek mindegyikének van K-val közös határpontja, de a hét sokszög közül semelyik kettőnek nincs közös belső pontja. (5 pont)
Megoldásvázlat. A sokszög három eltolt példányát elhelyezhetjük úgy, hogy páronként érintsék egymást. A három példány egymáshoz képesti eltolásait három vektor adja meg, amelyek összege 0:
Ezekkel a vektorokkal és ellentettjeivel eltolva K-t, kapjuk a feladat megoldását:
