Az 1999. decemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 224. Bizonyítsuk be, hogy tetszőleges pozitív a₁, a₂, ..., a_n számokra

(1)  

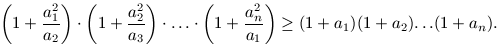
1. megoldásvázlat. Könnyen elllenőrizhető, hogy

(2)  

(Beszorzás és rendezés után az (a_i-a_i+1)²0 egyenlőtlenséget kapjuk.) A (2) egyenlőtlenséget i=1,2,...,n-re felírva és összezorozva éppen a bizonyítandó állítást kapjuk.

Csóka Endre (Debrecen, Fazekas M. Gimn., 9. o.)

2. megoldásvázlat. Az állítást teljes indukcióval bizonyítjuk. Ha n=1, akkor (1) mindkét oldalán 1+a₁ áll.

Tegyük fel, hogy az állítás igaz n=k-1 esetén. Ebből bebizonyítjuk n=(k+1)-re is.

Az a₁, ..., a_n számok ciklikus cseréjével a bizonyítandó állítás nem változik, ezért feltehetjük, hogy a_n az (egyik) legnagyobb. Írjuk fel az indukciós feltevést az a₁, ..., a_n-1 számokra:

(3)  

Ahhoz, hogy ebből (1) következzen, elégséges, ha

Beszorozva és rendezve:

(a_n+a_n-1²)(a₁+a_n²)a_n(1+a_n)(a₁+a_n-1²)

(a_n-a₁)(a_n-a_n-1)(a₁+a_n)0.

Mivel a_na₁ és a_na_n-1, a baloldalon mindhárom tényező nemnegatív.

3. megoldásvázlat. Tetszőleges H{1,2,...,n} nem üres halmaz esetén legyen

illetve legyen P₀=1.

(1) jobboldala beszorzva nem más, mint

(4)  

Jelölje H' azt a halmazt, amit úgy kapunk, hogy H mindegyik elemét 1-gyel növeljük modulo n (azaz n+1 helyett 1-et írunk). (1) baloldala beszorozva

(5)  

Azt kell tehát igazolnunk, hogy

(6)  

Megmutatjuk, hogy (6) következik az úgynevezett rendezési tételből (megtalálható pl. Matematikai Versenytételek, II. rész, 60-61.oldal; Tankönyvkiadó, Budapest, 1988):

Legyenek x₁, x₂, ..., x_n és y₁, y₂, ..., y_n pozitív valós számok, és jelentse z₁, z₂, ..., z_n a második sorozat egy permutációját. Az

S=x₁z₁+x₂z₂+...+x_nz_n

alakú összegek közül az a legnagyobb, amelyben a z₁,...,z_n számok ugyanúgy vannak rendezve, mint az x₁,...,x_n számok, vagyis x_i<x_j esetén z_iz_j. A legkisebb öszzeg pedig az, amelyben a z₁,...,z_n számok ellentétesen vannak rendezve, mint az x₁,...,x_n számok, vagyis x_i<x_j esetén z_iz_j.

Alkalmazzuk a rendezési tételt a P_H², az 1/P_H illetve az 1/P_H' (H{1,...,n}) számokra. Az 1/P_H alakú számok az 1/P_H' alakú számok egy permutációját adják, és rendezésük éppen ellentétes az P_H² alakú számokéval. Ezért

Baharev Ali (Vác, Boronkai Gy. Gimn., 12. o.) és

Gyenes Zoltán (Budapest, ELTE Apáczai Csere J. Gyak. Gimn., 12.o)

dolgozata alapján

A. 225. Jelölje S₁ és S₂ az 1, 2, ..., n számok páratlan, illetve páros osztói számának összegét. Igazoljuk, hogy

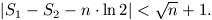
Megoldásvázlat. Tetszőleges k pozitív egész az 1,2,...,n számok közül pontosan darabnak osztója, ezért és . (Az összegek egy idő után csupa 0-ból állnak.)

Ismeretes, hogy vagyis

(1)  

Mivel tetszőleges k pozitív egészre

tetszőleges m pozitív egészre

(2)  

Legyen m tetszőleges pozitív egész. (1) és (2) felhasználásával

(3)  

Hasonlóképpen

(4)  

A (3) és (4) egyenlőtlenségek összevetéséből

(5)  

és ez tetszőleges m pozitív egészre igaz. Az választással azt kapjuk, hogy

A. 226. Adott egy gráf, amelynek csúcsai a pozitív egész számok és nem tartalmaz kxk-as teljes páros részgráfot. (k egy rögzített pozitív egész.) Igazoljuk, hogy létezik tetszőlegesen hosszú számtani sorozat, amelynek semelyik két eleme között nincs él.

Javasolta: Solymosi József, Budapest

Megoldásvázlat. Legyen m>1 tetszőleges pozitív egész. Bebizonyítjuk, hogy létezik olyan m hosszúságú számtani sorozat, amelynek semelyik két eleme között nincs él.

A továbbiakban, az egyszerűbb számolás kedvéért, tetszőleges valós x számra definiáljuk az számot a következőképpen:

Legyen N>max(k,3m) egy nagy pozitív egész. (Később pontosan definiáljuk.) Vizsgáljuk meg, hogy az 1,2,...,N csúcsú gráfban hány élt kell behúzni ahhoz, hogy tetszőleges m hosszú számtani sorozat valamelyik két eleme között legyen él. A d differenciájú, m hosszúságú számtani sorozatok száma N-(m-1)d. Az összes m hosszúságú számtani sorozatok száma pedig

Mindegyik számtani sorozathoz található egy él, ami két elem között halad. Egy él legfeljebb darab m hosszú számtani sorozat elemei között haladhat, ezért a gráf éleinek száma e>.

Most vizsgáljuk meg, hogy ha egy N pontú gráf nem tartalmaz kxk-as teljes páros részgráfot, akkor legfeljebb hány éle lehet.

Legyenek a csúcsok fokszámai f₁, f₂, ..., f_N; az élek száma e=(f₁+f₂+...+f_N)/2.

Számoljuk meg, hogy a gráf hány 1xk-as teljes páros részgráfot tartalmaz. Az i-edik csúcshoz, amelynek foka f_i, összesen -féleképpen választhatunk ki k darabot, amelyek szomszédosak vele. Az 1xkas teljes páros részgráfok száma tehát

Ha egy csúcs k-ast k alkalommal kiválasztanánk, akkor ez azt jelentené, hogy létezik egy kxk-as teljes páros részgráf. Ezért mindegyik csúcs k-ast legfeljebb k-1 alkalommal választottuk ki. Az 1xk-as teljes részgráfok száma tehát legfeljebb

Az függvény konvex, ezért felírhatjuk rá a Jensen-egyenlőtlenséget. A korábban kapott becsléssel együtt

Átrendezve

A kapott becsléseket összegezve

,

azaz N<(2m)^3k. Ha N ennél nagyobb, akkor az 1,2,...,N számok közül biztosan kiválasztható olyan számtani sorozat, amelynek semelyik két eleme között nincs él.