Az 1999. decemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 560. Egy cipó 25%-kal kisebb tömegű, mint egy fehér kenyér, ráadásul 20%-kal drágább. Igaz viszont, hogy a cipó az utolsó morzsáig elfogy, míg a kenyér 15%-a mindig ránkszárad. Ugyanakkora fogyasztást feltételezve hány százalékkal költünk többet, ha cipót veszünk, mint ha kenyeret?

Végeredmény: 36%-kal.

C. 561. Keressük meg azokat a p prímeket, amelyekre a p²+11 számnak pontosan 6 pozitív osztója van.

Megoldásvázlat. A páratlan négyzetszámok 4k+1 alakúak, a 3-mal nem osztható négyzetszámok pedig 3k+1 alakúak. Ezért, ha p>3, akkor p²+11 osztható 12-vel, ugyanakkor legalább 5²+11=36. Egy ilyen számnak biztosan van legalább 7 osztója: 1, 2, 3, 4, 6, 12, és önmaga. A 3-nál nagyobb prímszámok tehát nem megoldások.

p=2 esetén p²+11=15, aminek csak 4 osztója van.

p=3 esetén p²+11=20, aminek 6 osztója van.

Az egyetlen megoldás tehát p=3.

C. 562. Keressük meg azt a pozitív egész n számot, amelyre

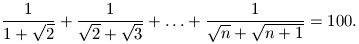
Megoldásvázlat. A nevezőket gyöktelenítve

A megoldás n=101²-1=10200.

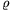C. 563. Egy O középpontú, r sugarú körben az átmérőnél kisebb húr legyen AB, az AO és BO sugarak által meghatározott kisebb körcikkbe beírt kör sugara pedig . Adjuk meg AB-t r és 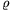segítségével.

Megoldásvázlat. Az ábra jelöléseit használva az OBE és OCD háromszögek hasonlóságából

C. 564. Egy téglatest oldalélei 26, 20 és 8 egység hosszúak. A 26x8-as lapok fölé építsünk olyan egyenes sátortetőket, amelyek ,,ferde'' éleinek hossza 13, ,,vízszintes'' éle pedig 20 egység. Mekkora a téglatest azon részének térfogata, amelyet úgy kapunk, hogy eltávolítjuk a téglából a sátortetőknek a téglatesthez illeszkedő lapjukra vonatkozó tükörképeit?

Megoldásvázlat. A feladat értelmezése problémát okozhatott, mert mi sátortető alatt nem az építészeti definíciót értettük, hanem a hétköznapit.

A "sátortető" legfontosabb adatait a Pithagorasz-tételből könnyen kiszámíthatjuk (1. ábra).

A két sátortető tükörképe egymásba lóg, mert magasságaik összege nagyobb 20 egységnél. Ezért ugyanazt az eredményt kapjuk, ha a sátortetőket 10 egység magasan elvágjuk, és két csonka sátortetőt távolítunk el (2. ábra).

Egy-egy csonka sátortetőt az ábrán látható módon szétbonthatjuk négy gúlára, négy darab háromszög alapú hasábra és egy téglatestre. Ezek térfogatát kivonva az eredeti téglatest térfogatából, megkapjuk a maradék test (3. ábra) térfogatát:

Test	Méret	Térfogat
Eredeti téglatest	8x20x26	4160
8 darab gúla	(10/3)x(5/2)x10	222
4 darab háromszög alapú hasáb	(5/2)x10x(4/3)	66
4 darab háromszög alapú hasáb	(10/3)x10x21	1400
2 darab téglatest	(4/3)x21x10	560
A maradék test		1911

A sátortetők elhagyásával kapott test térfogata tehát 1911 egység.